【2020年杭电暑假第一场】6755 Fibonacci Sum

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6755

前置技能

二项式定理、二次剩余、等比数列、欧拉降幂、阶乘逆元

参考：牌王无敌

题意

计算一个式子

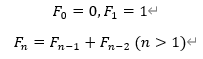
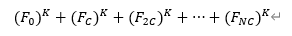
思路

由斐波那契通项公式得
$$F_n=\frac{1}{\sqrt{5}}((\frac{1+\sqrt{5}}{2}{)}^n-(\frac{1-\sqrt{5}}{2}{)}^n)$$
可以通过二次剩余的方法求出$\sqrt{5}=383008016或者616991993$，因为二次剩余的解有两个。下面顺便在给出二次剩余的板子，我也是花了一天的时间才弄懂计算过程。
我们让$A=\frac{1+\sqrt{5}}{2}、B=\frac{1-\sqrt{5}}{2}、D=\frac{1}{\sqrt{5}}$
进而利用逆元计算出
$A=691504013$
$B=308495997$
$D=276601605$

所以式子就变成了：
$$F_n=D(A^n-B^n)(mod1e9+9)$$
如果这样暴力算的话一定会T，因为N和C都达到了1e18。
我们先尝试列出前几项：
$当n=1时，F_c^k=D^k(A^c-B^c{)}^k$
用二项式定理展开后变为
$$F_c^k=D^k\sum _{i=0}^k(-1{)}^i{C}_k^i(A^c{)}^{k-i}(B^c{)}^i$$

$当n=2时F_{2c}^k=D^k(A^{2c}-B^{2c}{)}^k$
用二项式定理展开后变为
$$F_{2c}^k=D^k\sum _{i=0}^k(-1{)}^i{C}_k^i(A^{2c}{)}^{k-i}(B^{2c}{)}^i$$
$$F_{2c}^k=D^k\sum _{i=0}^k(-1{)}^i{C}_k^i(A^c{)}^{k-i}(B^c{)}^i{C}_k^i(A^c{)}^{k-i}(B^c{)}^i$$
所以当i相同时，这就是一个等比数列求和。

首项：$(-1{)}^i(A^{k-i}{B}^i{)}^c$
公比：$(A^{k-i}{B}^i{)}^c$

最后整理一下整个式子得
$$\sum _{i=0}^n{F}_{ic}^K=D^k\sum _{i=0}^K{C}_k^i\frac{(-1{)}^i(A^{k-i}{B}^i{)}^c(((A^{k-i}{B}^i{)}^c{)}^n-1)}{(A^{k-i}{B}^i{)}^c-1}$$

当公比为1时，$(A^{k-i}{B}^i{)}^c=1$，所以只要计算$C_k^i\ast (-1{)}^i\ast (A^{k-i}{B}^i{)}^c\ast n$

为了快速处理$C_m^n$，需要预处理1e5以内的阶乘和阶乘逆元。
$$C_m^n=\frac{m!}{n!\ast (m-n)!}=m!\ast inv[n!]\ast inv[(m-n)!]$$

公比的优化，因为随着i的增大，第$i$项和第$i+1$项相差$(\frac{B}{A}{)}^c$，所以我们率先算出$A$的逆元$invA$，就可以$O(1)$递推求出该公比，即：
$$q_{i+1}=qi\ast (\frac{B}{A}{)}^c$$

对于使用快速幂求$c$次方，可以使用欧拉降幂来优化时间，因为题目给的$mod$是个质数，即：
$$a^b=a^{b\%(1e9+9-1)}(mod1e9+9)$$

Code

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
typedef long double ld;
typedef pair<int, int> pdd;

#define INF 0x7f7f7f
#define mem(a,b) memset(a , b , sizeof(a))
#define FOR(i, x, n) for(int i = x;i <= n; i++)

 const ll mod = 1e9 + 9;
 const int maxn = 1e5;
// const double eps = 1e-6;

 const ll B = 308495997;
 const ll invA = 691504012;
 const ll A = 691504013;
 const ll D = 276601605;

 ll F[maxn + 10]; // 阶乘
 ll invF[maxn + 10]; // 阶乘逆元
 ll invn[maxn + 10];

 inline ll quick_pow(ll a, ll b) // 快速幂
 {
    
    
     ll ans = 1, base = a;
     while (b)
     {
    
    
         if (b & 1)
         {
    
    
             ans = ans * base % mod;
         }
         base = base * base % mod;
         b >>= 1;
     }
     return ans % mod;
 }
    
 inline void Init()
 {
    
    
     F[0] = F[1] = invF[0] = invF[1] = invn[0] = invn[1] = 1;
     for (int i = 2; i <= maxn; i++)
     {
    
    
         F[i] = F[i - 1] * i % mod;
         invn[i] = (mod - mod / i) * invn[mod % i] % mod;
         invF[i] = invF[i - 1] * invn[i] % mod;
     }
 }

 inline ll getC(int m, int n)
 {
    
    
     if (m < 0 || n < 0 || n > m)
         return 0;
     ll ans = F[m];
     ans = ans * invF[n] % mod;
     ans = ans * invF[m - n] % mod;
     return ans;
 }

 inline ll MOD(ll a, ll b)
 {
    
    
     a += b;
     if (a >= mod)
         a -= mod;
     return a;
 }

void solve()
{
    
    
    ll n, c, k;
    cin >> n >> c >> k;
    ll ans = 0;
    ll a1 = quick_pow(quick_pow(A, k), c % (mod - 1)) % mod; // 首项(公比)
    ll q = quick_pow(invA * B % mod, c % (mod - 1)) % mod; // 公比递推
    ll n1 = n % mod;
    ll n2 = n % (mod - 1); // 欧拉降幂使用
    ll a1power = quick_pow(a1, n2) % mod;
    ll qpower = quick_pow(q, n2) % mod;

    for (int i = 0; i <= k; i++)
    {
    
    
        ll sum = getC(k, i) % mod;
        if (i & 1)
            sum = mod - sum; // 负数
        if (a1 == 1) // 公比为1
        {
    
    
            ans = (ans + n1 * sum % mod) % mod;
        }
        else
        {
    
    
            sum = sum * (a1 * (a1power - 1 + mod) % mod) % mod;
            sum = sum * quick_pow(a1 - 1, mod - 2) % mod;
            ans = MOD(ans, sum);
        }
        a1 = (a1 * q) % mod; // 更换公比
        a1power = a1power * qpower % mod;
    }
    cout << ans * quick_pow(D, k) % mod << endl;
}

signed main()
{
    
    
    ios_base::sync_with_stdio(false);
    //cin.tie(nullptr);
    //cout.tie(nullptr);
#ifdef FZT_ACM_LOCAL
   // freopen("in.txt", "r", stdin);
   // freopen("out.txt", "w", stdout);
#else
    ios::sync_with_stdio(false);
    int T = 1;
    cin >> T;
    Init();         
    while (T--)
        solve();
#endif
    return 0;
}

二次剩余板子

#include <iostream>
#include <ctime>

using namespace std;

typedef long long ll;

typedef struct{
    
    
    ll x, y; // 把求出来的w作为虚部，则为a + bw
}num;

num num_mul(num a, num b, ll w, ll p) // 复数乘法
{
    
    
    num ans = {
    
    0, 0};
    ans.x = (a.x * b.x % p + a.y * b.y % p * w % p + p) % p;
    ans.y = (a.x * b.y % p + a.y * b.x % p + p) % p;
    return ans;
} 

ll num_pow(num a, ll b, ll w, ll p) // 复数快速幂
{
    
    
    num ans = {
    
    1, 0};
    while(b)
    {
    
    
        if(b & 1)
        {
    
    
            ans = num_mul(ans, a, w, p);
        }
        a = num_mul(a, a, w, p);
        b >>= 1;
    }
    return ans.x % p;
}

ll quick_pow(ll a, ll b, ll p) // 快速幂求解
{
    
    
    ll ans = 1, base = a;
    while(b)
    {
    
    
        if(b & 1)
        {
    
    
            ans = ans * base % p;
        }
        base = base * base % p;
        b >>= 1;
    }
    return ans % p;
}

ll legendre(ll a, ll p) // 勒让德符号 = {1, -1, 0}
{
    
    
    return quick_pow(a, (p - 1) >> 1, p);
    
}

ll Cipolla(ll n, ll p) // 输入a和p，是否存在x使得x^2 = a (mod p)，存在二次剩余返回x，存在二次非剩余返回-1     注意：p是奇质数
{
    
    
    n %= p;
    if(n == 0)
        return 0;
    if(p == 2)
        return 1;
    if(legendre(n, p) + 1 == p) // 二次非剩余
        return -1;
    
    ll a, w; 
    
    while(true) // 找出a，求出w，随机成功的概率是50%，所以数学期望是2
    {
    
    
        a = rand() % p;
        w = ((a * a - n) % p + p) % p;
        if(legendre(w, p) + 1 == p) // 找到w，非二次剩余条件
            break;
    }
    num x = {
    
    a, 1};   
    return num_pow(x, (p + 1) >> 1, w, p) % p; // 计算x,一个解是x，另一个解是p-x，这里的w其实要开方，但是由拉格朗日定理可知虚部为0，所以最终答案就是对x的实部用快速幂求解
}

int main()
{
    
    
    ll n, p;
    cin >> n >> p;
    srand((unsigned)time(NULL));
    cout << Cipolla(n, p) << endl;
    return 0;
}

后记

感谢牌王的亲情指导和博客