目录
卷积神经网络（Convolutional Neural Network，CNN）
第二章：感应机（人工神经元）
感知机作为神经网络起源的算法
二. 感知机
概念：感知机其实就是流与不流的问题，流就是1不流就是0、0 对应“不传递信号”，1对应“传递信号”
x1，x2是输入，y是输出，w1，w2是权值，x*w之和超过阀值θ时才会激活y
2. 简单逻辑电路
2.1简单逻辑电路
这里与门、与非门、或门的逻辑电路就比较简单，就是根据与或非，然后结合上面感知器的公式求和是否超过阀值来激活神经元
2.2代码实现：
与门实现：其他也是类似的
2.3导入权重和偏置
如果根据上式，θ是个负数的话，我们可以把他换成-b，转换得到
偏置和权重的作用是不一样的，权重是控制输入信号的重要性的参数，而偏置是调整神经元被激活的容易程度（输出信号为1的程度）的参数
numpy代码实现：
注意：这部分权重是根据经验计算而来的
2.4感知机局限性
曲线分割而成的空间称为非线性空间，由直线分割而成的空间称为线性空间
其中感知机可以表示与、或和与非门，他们都是线性的，但是异或却不是线性的，不能由感知机单层表示,但是可以多重感知机表示。
2.5多层感知机实现（解决异或门）
在梳理逻辑的学习里-这种多重结构解决了异或门
代码实现：
逻辑如下：
假设，异或门是一种多层结构的神经网络。这里，将最左边的 一列称为第0层，中间的一列称为第1层，最右边的一列称为第2层
感知机通过叠加层能够进行非线性的表示，理论上还可以表示计算机进行的处理
2.6 小结
是数理课本的内容，最主要是能够理解 感知机 与神经网路的关系
三、神经网络
解决问题：上一章能用与或非解决各种函数问题，但是权重是人工设定的，本章开始根据神经网络的实现，利用已有的数据学习合适的权重作为参数来解决上面的问题。
3.1 从感知机到神经网络
3.1.1神经网络例子：
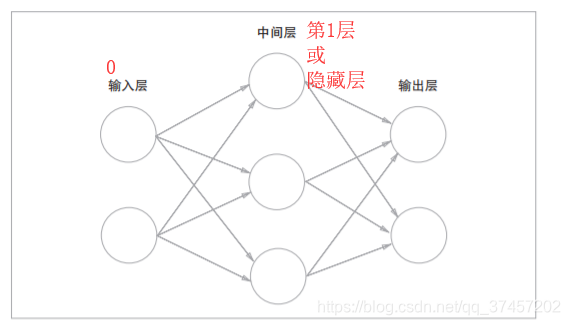
神经网络实际跟感知机一样
3.1.2函数转换：
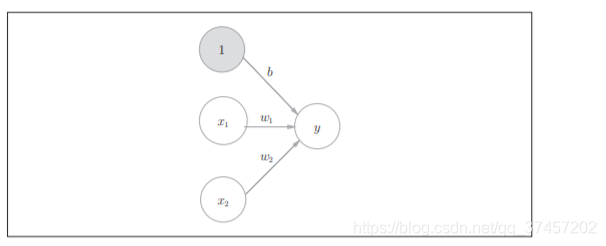
借鉴：方同学整理的公式图
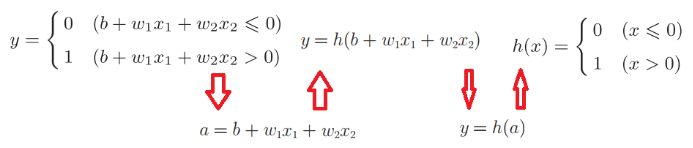
根据上图的函数转换，我们就能转换为h(x)，这就是激活函数
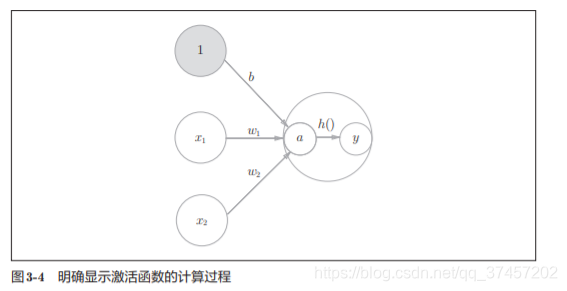
激活函数是连接感知机和神经网络的桥梁
3.2激活函数
3.2.1激活函数类型：
激活函数以阈值为界，一旦输入超过阈值，就切换输出。 这样的函数称为“阶跃函数”。
激活函数分为阶跃函数和sigmoid函数，其中阶跃函数就是当输入值超过某一阀值时就换转变输出。
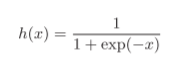
其中exp(−x)表示的意思，h(x)也常用语分类的损失函数
代码实现：
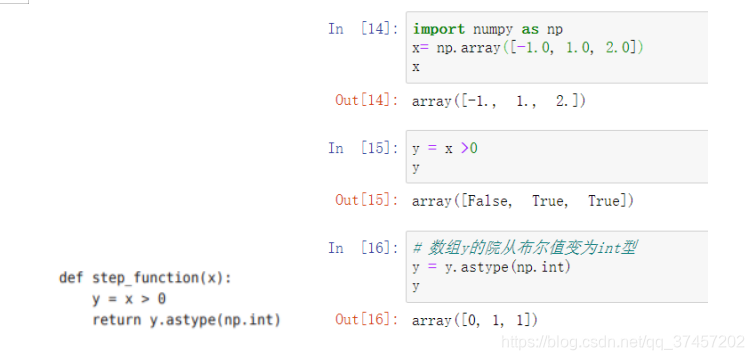
3.2.3 阶级函数的图形
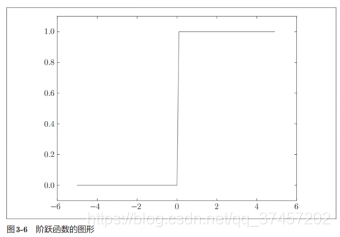
阶跃函数与图像实现：
sigmoid函数图像：
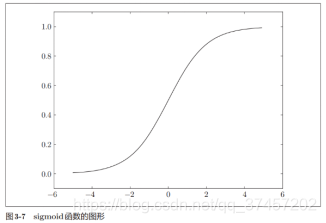
3.2.2阶跃函数和sigmoid函数对比：
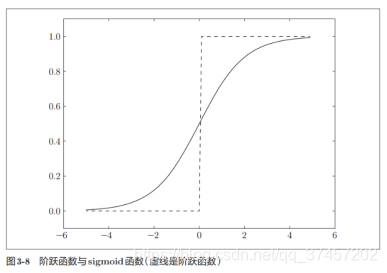
| 阶跃函数 | sigmoid函数 |
|---|---|
| 非平滑的 | 平滑的 |
| 只有2个值（二元值） | 无限个实数值 |
他们两者的相似点在于他们都处在0-1范围之间
神经网络的激活函数必须使用非线性函数。
另外sigmoid是非线性的曲线，不像线性函数（直线）h(x)=cx(c是常数)，因为线性函数在多层感知机中是没有隐藏层的，如
一样是y=ax，无法发挥多层的优势。
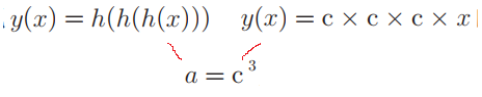
3.2.3ReLU函数：
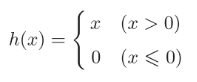
大于0时直接输出x，小于等于0时输出0
函数实现：其中maxinum返回最大值
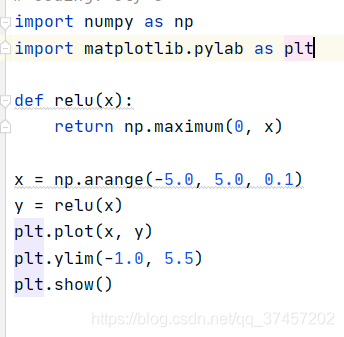
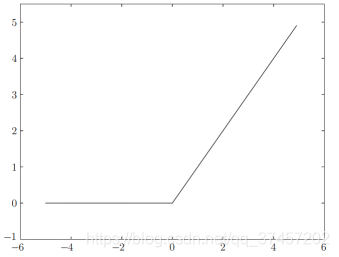
实现效果如图：
3.3多维数组的运算：
np.ndim(A) 输出A矩阵维数
np.shape 输出形状，既有几个构成。结果是个元组（tuple）。
3.3.1神经网络的内积：
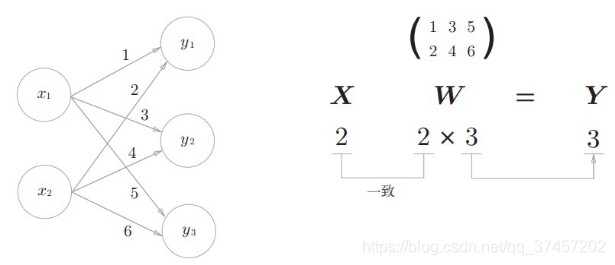
使用np.dot（多维数组的点积），矩阵运算而已
3.4.三层神经网络的实现
符号含义：
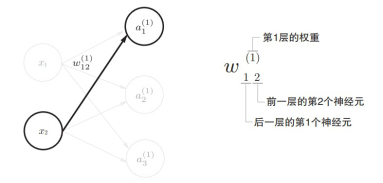
原理分析：
1）实现第0层到第一层：
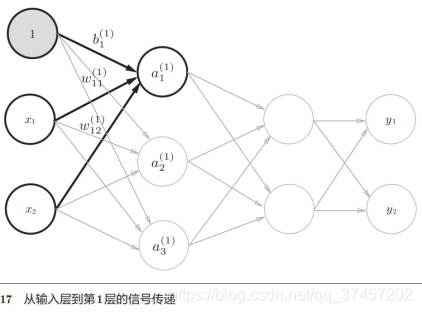
我们知道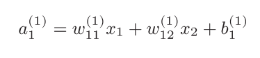
所以有第一层的加权：
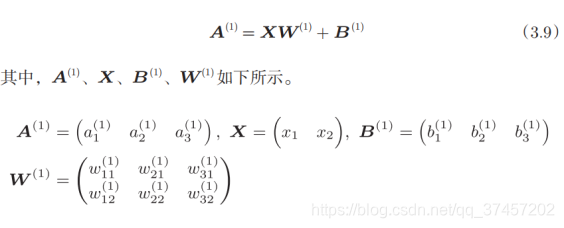
代码实现：
2）实现下图a1到z1构成激活函数h()的转变（sigmoid函数）：
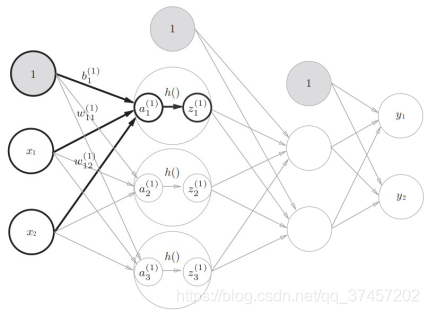
代码实现：
3）同理第一层到第二层一样，直接重复上面步骤：
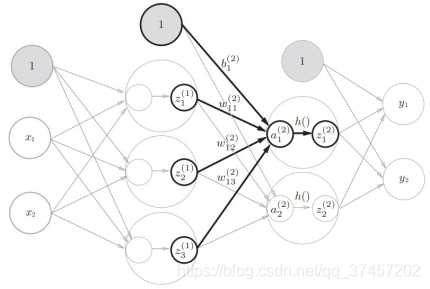
代码实现：
4）第2层到第三层（输出层）也跟上面步骤基本一致，但激活函数不同：
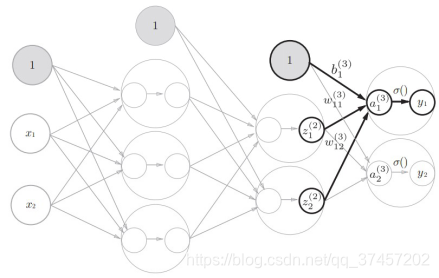
5）总体代码实现：
注意：一般地，回归问题可以使用恒等函数，二元分类问题可以使用 sigmoid函数， 多元分类问题可以使用 softmax函数。3.5输出层的设计：
3.5.1三中输出函数类型
1）恒等函数：就是直接原样输出，用在回归问题上
2）sigmoid函数：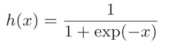
，用在二元分类问题上。
3）softmax函数：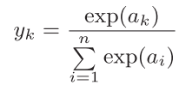
，用在多元分类问题上。
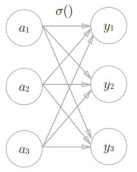
其中softmax函数表示在各输出之间都有收到输入信号的影响，如图：
代码实现：
3.5.2softmax函数溢出问题
我们都知道e^x当x很大时会出现爆炸性增长，这会导致溢出，所以我们要改进
3.5.3softmax函数特征：
我们可以看到输出的y都在0-1之间，且它们的和为1，所以我们可以把他转为概率问题，也就是说输出的越大，他的概率越高，从上图可以看出，y[2]最大，所以答案是第2个类别；另外e^x是一个单调递增函数，所以上例中a元素的大小关系和y的大小关系不变，y[2]最大，所以我们在实际上根本不需要softmax函数，直接看a元素就能知道哪个概率最大了（因为softmax需要指数运算，计算量挺大的）。
3.5.4输出层的神经元数量
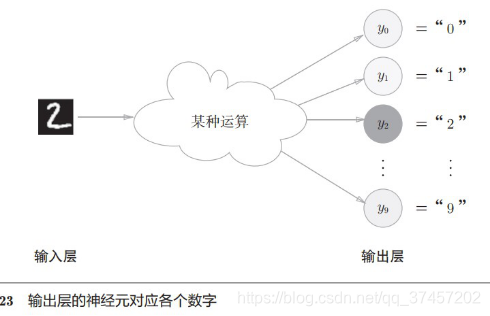
由上图可以知道，输出神经元数量由类别数量决定，如输出结果为0-9这10个类别，那么神经元输出则为10个。
3.6手写数字识别
接下来，我们将我们的算法用于实际应用中，经典例子手写数字识别
代码注释如下，就不一一描述了。
load_mnist函数以“(训练图像 ,训练标签 )，(测试图像，测试标签 )”的 形式返回读入的MNIST数据。
显示数字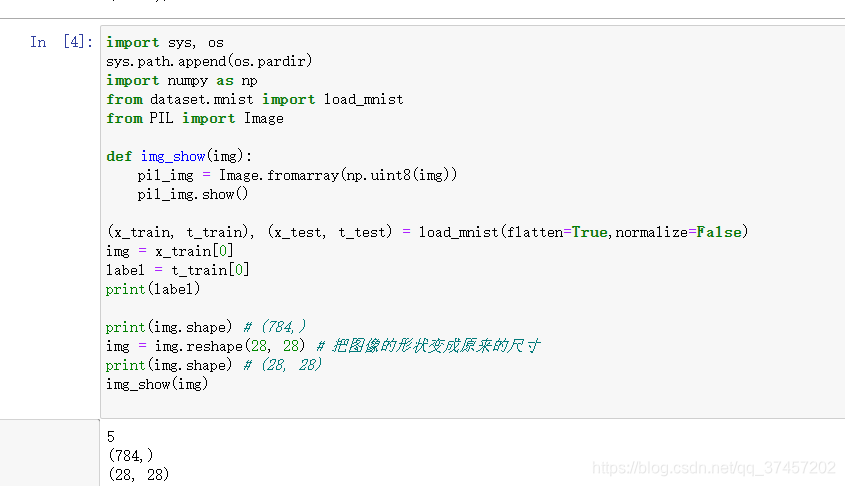
神经网路输出
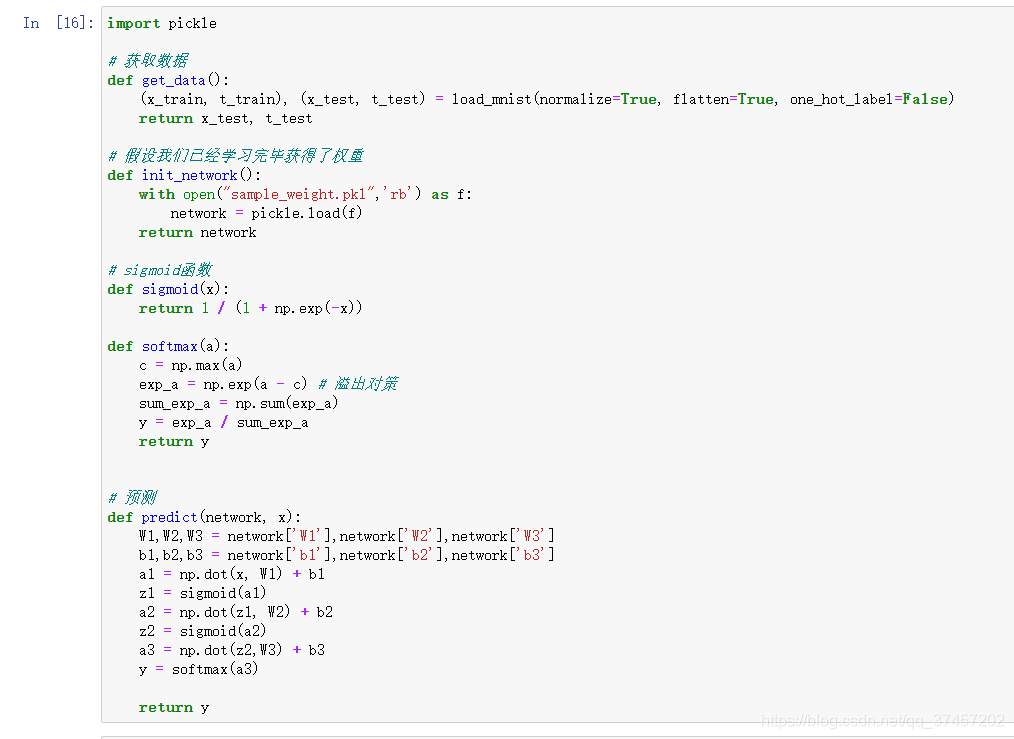
单处理与批处理
从上面的例子，我们知道输入层有784个神经元（28*28），输出层有10个神经元，假定隐藏层的1-2层有50个和100个神经元，我们有下面代码处理：
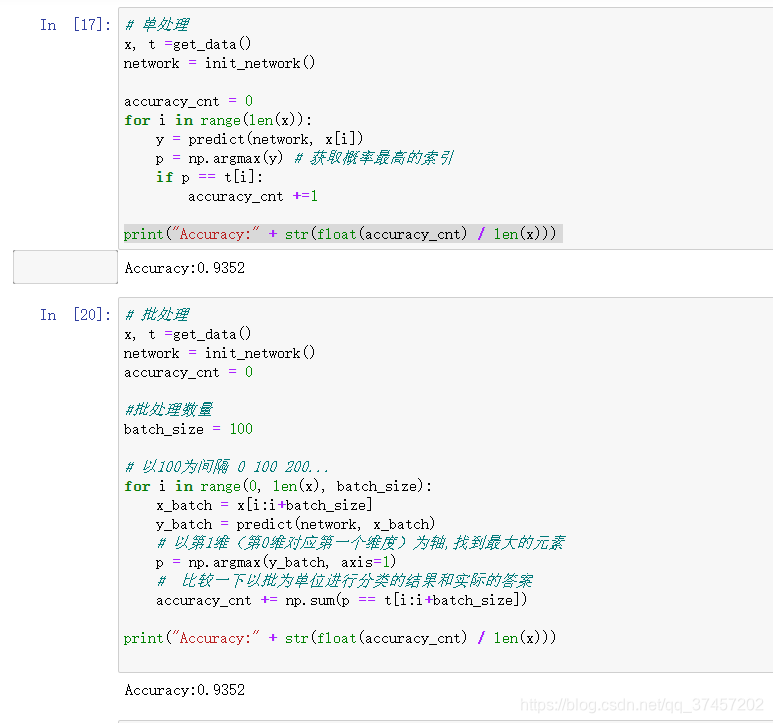
1）单处理：
利用上面一有的函数知识，我们现在正式可以判断其训练后的图片和标签之间的精确度啦：
2）批处理：
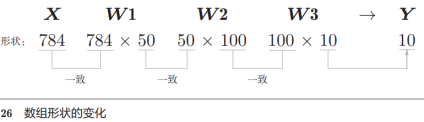
从上面（上图）的例子，我们知道1个图像输入（1*28*28）和输出（10个类别的概率）之后的矩阵形状
下面我们把以上面的例子一次性打包成100个图像进行计算
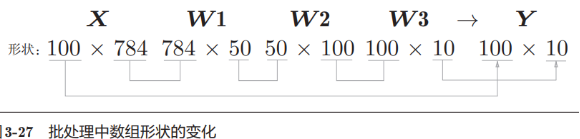
批处理的好处：每次我们计算一张时要io一次只拿1个图片，现在我们把一次的io拿100张来计算，因为计算速度比io速度快，所以批处理会在整体计算上变得更快
代码实现：
小结：
与上一章一样，我们不考虑具体权重如何求出，通过每一层的函数进行输出，这样就构成了一个简单的神经网络。
后期会对上面的参数进行讲解
前言：
上一章讲了神经网络前向传播内容，这一章讲如何根据数据训练出相关权重参数的过程。我们在实战中直接得出了参数权重，接下爱我们要学习
4.1从数据中学习
介绍神经网络的学习，即利用数据决定参数值的方法。我们将针对上一个实验的训练集进行学习
4.1.1数据驱动
图像的特征量通常表示为向量的形式。
前面学习过分类算法SVM以及KNN，我们手动提取特征向量。
深 度 学 习 有 时 也 称 为 端 到 端 机 器 学 习（end-to-end machine learning）。这里所说的端到端是指从一端到另一端的意思，也就是 从原始数据（输入）中获得目标结果（输出）的意思。
神经网络的优点是对所有的问题都可以用同样的流程来解决。
4.1.2训练数据和测试数据
1.训练数据和测试数据：训练数据用来训练模型的，而测试数据就是不包含在训练模型内的数据，用来评判训练后模型好坏的数据。
2.泛化能力：如果测试的成绩好那么他的泛化能力就好。
3.过拟合：适应训练数据强，但泛化能力弱。
4.2损失函数
神经网络的学习的目的就是以该损失函数为基准，找出能使它 的值达到最小的权重参数
种评判方法均方误差和交叉熵误差
4.2.1均方误差
实现代码：
4.2.2交叉熵误差
交叉熵误差的值是由正确解标签所对应的输出结果决定的
实现代码：
4.2.3mini-batch学习
单个单个计算的话，数据处理时间过长，我们希望时间大部分花费咋计算上面。计算所有数据的（损失函数值的和/总数）的平均损失函数值
分析上一个实验的数据包
随机抽取10笔
为了找到使损失函数的值尽可能小的地方，需要计算参数的导数（确切地讲是梯度），然后以这个导数为指引，
逐步更新参数的值。
4.2.5为什么要设定损失函数
因为损失函数可导且连续，便于调试。
以一个例子，比如有100个训练数据进行测试，发现精度为32%，如果以识别精度为指标，那么稍微修改权重参数精度也只会是32%，稍微改动大一点点权重参数精度可能直接变为33%，这种是离散不连续的变化；而损失函数不一样，稍微改变权重关系时，损失函数值就会立刻改变（如0.9524变为0.9612），这种值是连续性的，因为离散型的变化其导数（斜率）一般都为0，而连续型的变化导数一般不为0，所以能很容易判别出权重参数变化时的模型好坏。
4.3数值微分
4.3.1导数
1.10e-50精度会有误差，比如python的float精度为小数点后4位，这里已经是50位了，所以要改成10e-4 舍入误差
2.f(x+h)-f(x)/h（向前差分）这个误差也很大，因为根据1的改变，h不是一个趋近于0的数，所以误差变大，应该用中心法改成f(x+h)-f(x-h)/2h（中心差分）
利用微小的差分求导数的过程称为数值微分（numerical differentiation）
数值微分（数值梯度）
改进后代码
中值定理的感觉
注意：
这种利用微小差分的导数过程为数值微分，而用数学公式推导的如y=x²导数为y=2x这种交解析性求导，这种叫做真导数
4.3.2一个微分的例子
如y=0.01x²+0.1x的导数实现
可以发现改进后的微分代码误差非常小
数值微分代码：
4.3.3偏导数
比如实现
的偏导数
先看这个函数的代码实现与图像：
偏导数实现：原理其实跟一元导数一样，就是带入一个真值消除一个变量而已
公式难在数值微分，肉眼偏导验算一下，第一条公式为2*X0
4.4梯度
在刚才的例子中，我们按变量分别计算了x0和x1的偏导数。现在，我 们希望一起计算x0和x1的偏导数。比如
比如我们求一个函数y=x0²+x1²变量有x0，x1，当我们对他全部变量（这里最多只有2个）进行偏导汇总而成的变量叫梯度。
梯度指向的图
从这个图可以看出，梯度指向的点的函数值越来越小，反之越来越大，这是梯度重要性质！
4.4.1梯度法
寻找最小值的梯度法称为梯度下降法（gradient descent method）， 寻找最大值的梯度法称为梯度上升法（gradient ascent method）。
神经网络（深度学习）中，梯度法主要是指梯度下降法
从上面的梯度我们可以知道梯度其实就是寻找梯度为0的地方，但是梯度为0不一定是最小值(高数里的靶点)，他可能是极小值或者是鞍点（某方向看是极小值，另一方向看是极大值，导数为0的点），所以我们可以计算一次梯度后再次计算一次梯度，这样最后就能找到真正的最小值点了，这就是梯度法。
学习率决定在一次学习中，应该学习多少，以及在多大程度上更新参数。
注意：找最小其实跟找最大是一样的，就是取负的问题而已，不用太在意这个。
（梯度下降法）代码实现：
numerical_gradient(f,x)会求函数的梯度，用该梯度乘以学习率得到的值进行更新操作，由step_num指定重复的 次数。
这个例子中得到的最后的x值都是非常小的数，都几乎趋向于0，根据解析式方式（自己动笔试试）我们知道最小值为（0,0），跟上面的例子几乎一致（实际的例子中最小值不一定是0）。
每次求导后的过程：
实现代码：
# coding: utf-8
import numpy as np
import matplotlib.pylab as plt
from gradient_2d import numerical_gradient #求梯度，原理与数值微分相同
#梯度下降法
def gradient_descent(f, init_x, lr=0.01, step_num=100):
x = init_x
x_history = []
for i in range(step_num):
# 记录前一个x,用于绘图痕迹
x_history.append( x.copy() )
# 梯度下降法，为梯度乘以学习率
grad = numerical_gradient(f, x)
x -= lr * grad
return x, np.array(x_history)
# 求偏导，np.sum(x**2)
def function_2(x):
return x[0]**2 + x[1]**2
init_x = np.array([-3.0, 4.0])
# 学习率为0.1
lr = 0.1
# 梯度法的重复次数
step_num = 20
x, x_history = gradient_descent(function_2, init_x, lr=lr, step_num=step_num)
plt.plot( [-5, 5], [0,0], '--b')
plt.plot( [0,0], [-5, 5], '--b')
plt.plot(x_history[:,0], x_history[:,1], 'o')
plt.xlim(-3.5, 3.5)
plt.ylim(-4.5, 4.5)
plt.xlabel("X0")
plt.ylabel("X1")
plt.show()
这里有个学习率太大 太小的例子：
太大时结果会发散成很大的数，太小的话结果几乎没更新就结束了
所以学习率n太大太小都不好，学习率被称为超参数，一般认为多次设定后取一个合理值。
学习率这样的参数称为超参数。
相对于神经网络的权重参数是通过训练 数据和学习算法自动获得的，学习率这样的超参数则是人工设定的。
4.4.2神经网络的梯度
所说的梯度是指损失函数关于权重参数的梯度
如图，我们有2*3的W权重参数，L为损失函数，梯度用
表示，如图：
为simpleNet的类（源代码在ch04/gradient_simplenet.py 中
代码实现：
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 为了导入父目录中的文件而进行的设定
import numpy as np
from common.functions import softmax, cross_entropy_error
from common.gradient import numerical_gradient
class simpleNet:
def __init__(self):
# 初始化2*3权重参数
self.W = np.random.randn(2,3)
def predict(self, x):
# 一层 权重乘以变量 == 一层感知机
return np.dot(x, self.W)
def loss(self, x, t):
# 计算交叉熵softmax()函数的损失值
z = self.predict(x)
y = softmax(z)
loss = cross_entropy_error(y, t)
return loss
x = np.array([0.6, 0.9])
t = np.array([0, 0, 1])
net = simpleNet()
f = lambda w: net.loss(x, t)
dW = numerical_gradient(f, net.W)
print(dW)
4.5 学习算法的实现
随机梯度下降法（stochastic gradient descent）。“随机”指的是“随机选择的” 的意思，因此，随机梯度下降法是“对随机选择的数据进行的梯度下降法”。简称SGD
实现代码：
4.5.1 2层神经网络的类
two_layer_net:
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
from common.functions import *
from common.gradient import numerical_gradient
class TwoLayerNet:
"""
从第1个参数开始，依次表示:
输入层的神经元数、隐藏层的神经元数、输出层的神经元数
输入图像大小784 输出10个数字（0-9）
"""
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
# 初始化权重，是有要求的但是后面在补上
self.params = {}
# params变量中保存了该神经网络所需的全部参数
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
def predict(self, x):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
return y
# x:输入数据, t:监督数据
def loss(self, x, t):
y = self.predict(x)
return cross_entropy_error(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
# x:输入数据, t:监督数据
# numerical_gradient(self, x, t)
# 基于数值微分计算参数的梯度。
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
# 使用误差反向传播法计算梯度
def gradient(self, x, t):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
grads = {}
batch_num = x.shape[0]
# forward
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
# backward
dy = (y - t) / batch_num
grads['W2'] = np.dot(z1.T, dy)
grads['b2'] = np.sum(dy, axis=0)
da1 = np.dot(dy, W2.T)
dz1 = sigmoid_grad(a1) * da1
grads['W1'] = np.dot(x.T, dz1)
grads['b1'] = np.sum(dz1, axis=0)
return grads
4.5.2 mini-batch的实现
类：train_neuralnet：
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet
# 读入数据
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
# 超参数
iters_num = 10000 # 适当设定循环的次数
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
train_acc_list = []
test_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
for i in range(iters_num):
# 获取mini-batch
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 计算梯度
#grad = network.numerical_gradient(x_batch, t_batch)
# 高速版
grad = network.gradient(x_batch, t_batch)
# 更新参数
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
# 记录学习过程
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))
# 绘制图形
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, label='train acc')
plt.plot(x, test_acc_list, label='test acc', linestyle='--')
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()可以发现随着学习的进行，损失函数的值在不断减小。这 是学习正常进行的信号，表示神经网络的权重参数在逐渐拟合数据。也就是 说，神经网络的确在学习！通过反复地向它浇灌（输入）数据，神经网络正 在逐渐向最优参数靠近。
实线表示训练数据的识别精度，虚线表示测试数据的识别精 度
4.5.3 基于测试数据的评价
光看这个结果还不能说明该神经网络在 其他数据集上也一定能有同等程度的表现。
神经网络的学习中，必须确认是否能够正确识别训练数据以外的其他数 据，即确认是否会发生过拟合。
要评价神经网络的泛 化能力，就必须使用不包含在训练数据中的数据
epoch是一个单位。一个 epoch表示学习中所有训练数据均被使用过 一次时的更新次数。比如，对于 10000笔训练数据，用大小为 100 笔数据的mini-batch进行学习时，重复随机梯度下降法 100次，所 有的训练数据就都被“看过”了A。此时，100次就是一个 epoch。
代码在上面：
之所以要计算每一个epoch的识别精度，是因 为如果在for语句的循环中一直计算识别精度，会花费太多时间
没有必要那么频繁地记录识别精度（只要从大方向上大致把握识别精度的推 移就可以了）
小结：
本章所学的内容
- 机器学习中使用的数据集分为训练数据和测试数据。
- 神经网络用训练数据进行学习，并用测试数据评价学习到的模型的 泛化能力。
- 神经网络的学习以损失函数为指标，更新权重参数，以使损失函数的值减小。
- 利用某个给定的微小值的差分求导数的过程，称为数值微分。
- 利用数值微分，可以计算权重参数的梯度。
- 数值微分虽然费时间，但是实现起来很简单。
需要注意的时候，你会觉得比较多内容这一章，建议书写一下：
| 名称 | 函数 |
|---|---|
| 数值微分 | numerical_diff（x） |
 偏导数 |
function_2(x) |
| 偏导数 |  |
 梯度 |
numerical_gradient（f,x） |
| 梯度下降法 | gradient_descent(f, init_x, lr=0.01, step_num=100) |
下一章中要实现的稍 微复杂一些的误差反向传播法可以高速地计算梯度。
误差反向传播法
前言：
数值微 分虽然简单，也容易实现，但缺点是计算上比较费时间。本章我们将学习一 个能够高效计算权重参数的梯度的方法——误差反向传播法
正确理解误差反向传播法：一种是基于数学式； 另一种是基于计算图（computational graph）
5.1 计算
5.1.1 用计算图求解
节点用○表示，○中是计算的内容。
也可以表示为:
5.2 链式法则
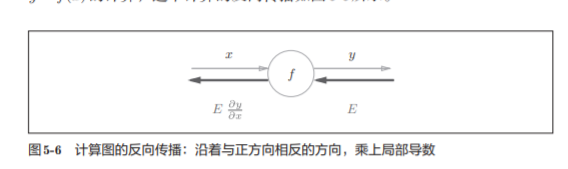
5.2.1 计算图的反向传播
5.2.2 什么是链式法则
以高数里面的复合函数为励志
z = (x + y) ^2
规则：
如果某个函数由复合函数表示，则该复合函数的导数可以用构成复 合函数的各个函数的导数的乘积表示。
5.2.3 链式法则和计算图
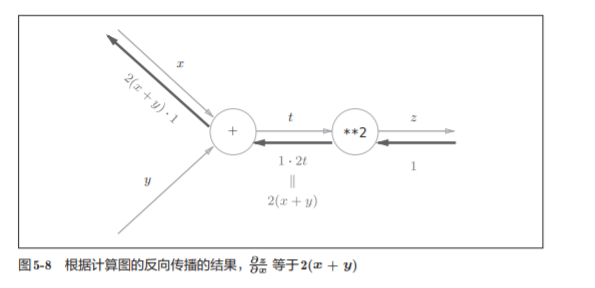
我们尝试将式（5.4）的链式法则的计算用计算图表示出来
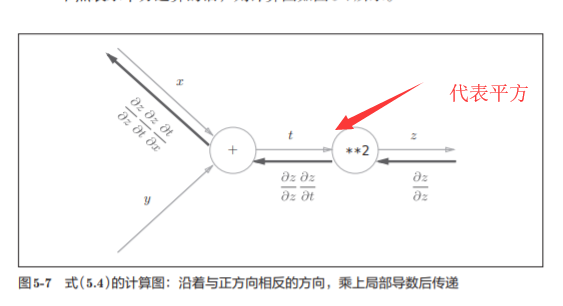
有上面的公式运算易得：
5.3 反向传播
上一节介绍了计算图的反向传播是基于链式法则成立的。下面以+ * 等运算未例子
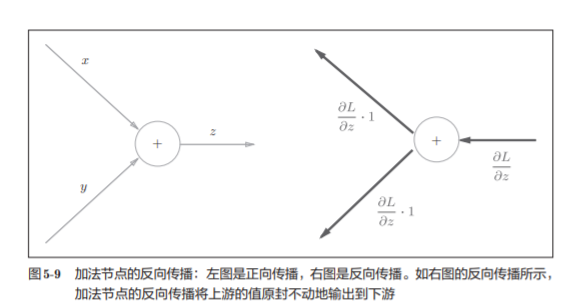
5.3.1 加法节点的反向传播
z = x + y的导数
则得到：
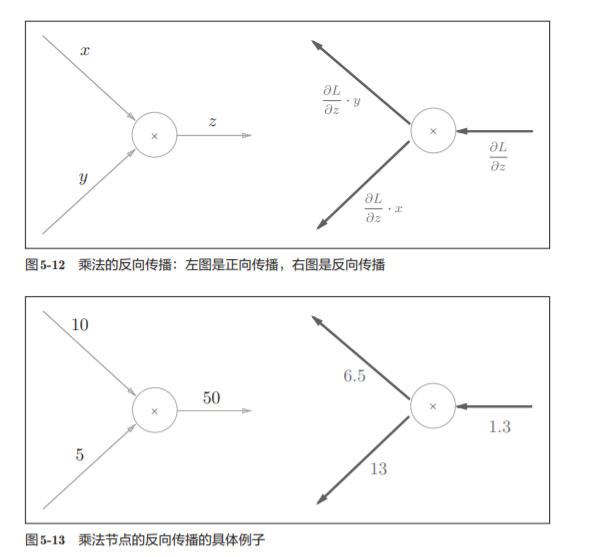
5.3.2 乘法节点的反向传播
“翻转值”---太直观了吧 就是xy求偏导的时候出现的情况
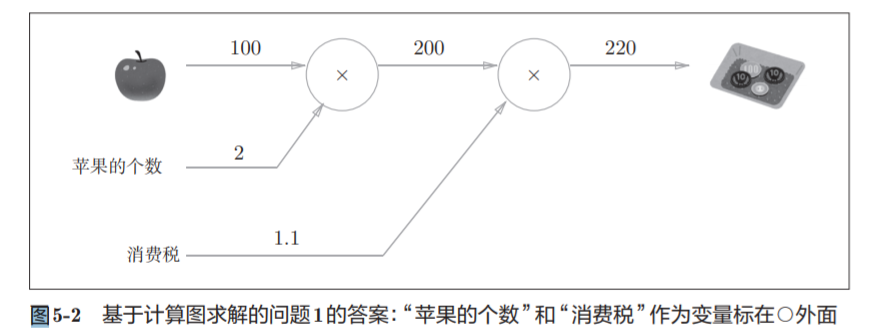
5.3.3 苹果的例子
练习：
答案：
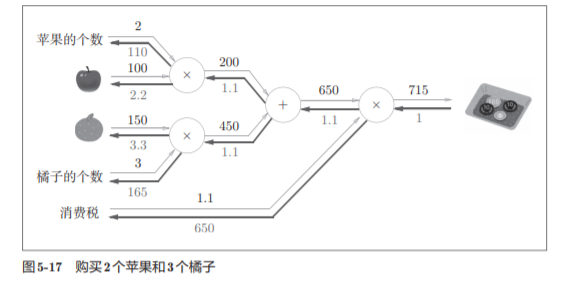
5.4 简单层的实现
乘法节点称为“乘法层”（MulLayer），加法节点称为“加法层”
5.4.1 乘法层的实现
举个栗子：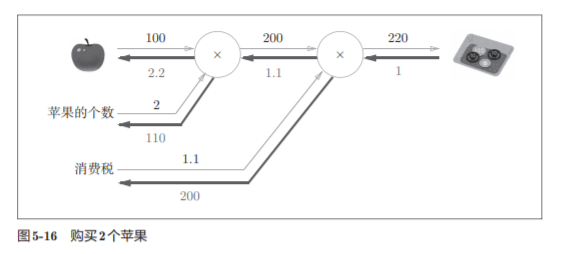
实现代码：
注意： 每一层 要分开
各个变量的导数可由backward()求出
5.4.2 加法层的实现
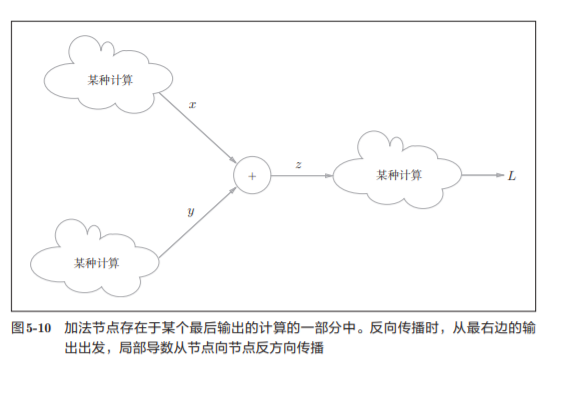
加法层的forward()接收x和y两个参数，将它 们相加后输出。
backward()将上游传来的导数（dout）原封不动地传递给下游
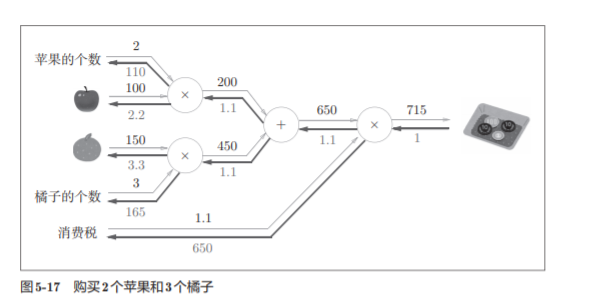
实现代码：
5.5 激活函数层的实现
们将计算图的思路应用到神经网络中。
我们把构成神经 网络的层实现为一个类。先来实现激活函数的ReLU层和Sigmoid层
5.5.1 ReLU层
在神经网络的层的实现中，一般假定forward() 和backward()的参数是NumPy数组。
实现代码：
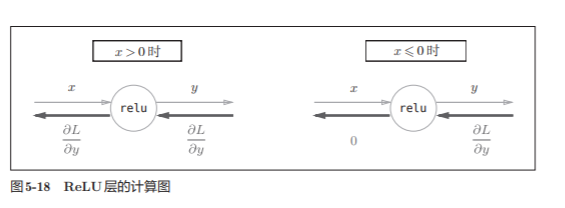
实现代码：
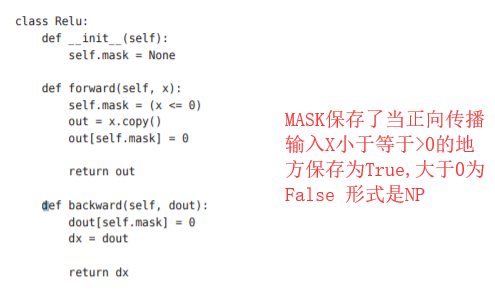
关于（x<=0）的解释
如果正向传播时的输入值小于等于0，则反向传播的值为0。 因此，反向传播中会使用正向传播时保存的mask，将从上游传来的dout的 mask中的元素为True的地方设为
5.5.2 Sigmoid层
实现sigmoid函数。sigmoid函数由式（5.9）表示
计算图表示式（5.9）的话，则如图5-19所示
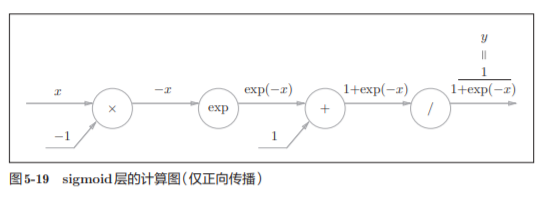
出现了新的“exp”和“/”节点，分别进行y = exp(x)，y=1/x
接下来计算他的方向传播
分为四个步骤，上书本的图比较直观
步骤1:
反向传播时，会将上游的值乘以−y 2 （正向传播的输出的 平方乘以−1后的值）后，再传给下游。
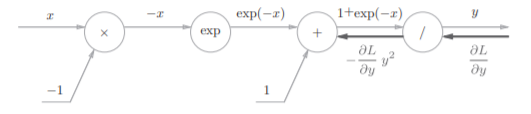
步骤2
“+”节点将上游的值原封不动地传给下游。计算图如下所示。
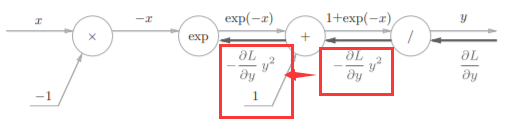
步骤3
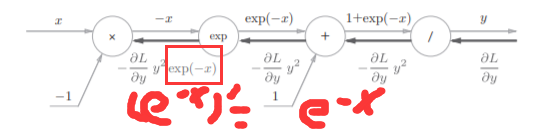
步骤4
乘法的话就只需要做一下翻转就可以了
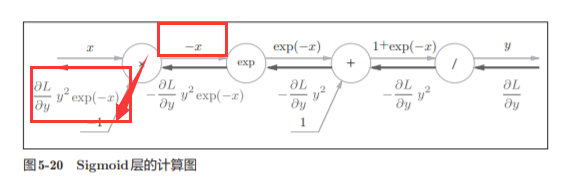
最后我们可以的得到：
因此，我们发现，我们通过正向传播的x和y就可以求出这个公式的数值
简洁版的计算图可以省略反向传播中的计算过程，因此计算效率更高
，可以不用在意Sigmoid层中琐碎的细节，而只需要 专注它的输入和输出
图5-21所表示的Sigmoid层的反向传播，只根据正向传播的输出 就能计算出来
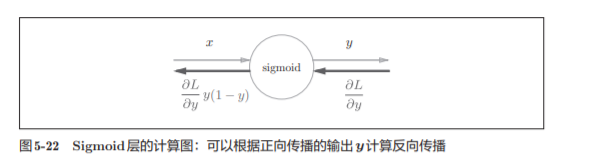
5.6 Affine/Softmax层的实现
神经网络的正向传播中，为了计算加权信号的总和，使用了矩阵的乘 积运算
神经元的加权和可以用Y = np.dot(X, W) + B
X和W 的乘积必须使对应维度的元素个数一致。
注意这里不是2行矩阵相乘法的意思
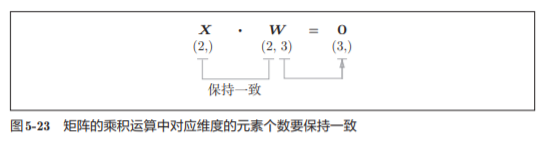
神经网络的正向传播中进行的矩阵的乘积运算在几何学领域被称为“仿射变换”A。因此，这里将进行仿射变换的处理实现为“Affine层”。
np.dot(X, W) + B的运算可用图5-24 所示的计算图表示出来
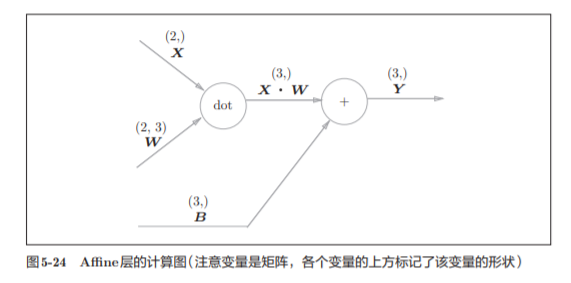
之前我们见到的计算图中各个节点间流动的是标量，而这个例子中各个节点 间传播的是矩阵
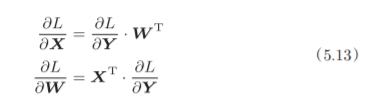
为什么要注意矩阵的形状呢？因为矩阵的乘积运算要求对应维度的元素 个数保持一致，通过确认一致性，就可以导出式（5.13）。
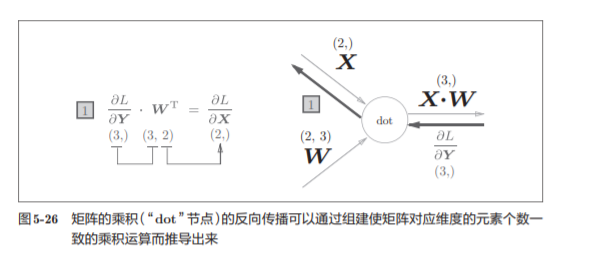
5.6.2 批版本的Affine层
在我们考虑N 个数据一起进行正向传播的情况，也就是批版本的Affi ne层。
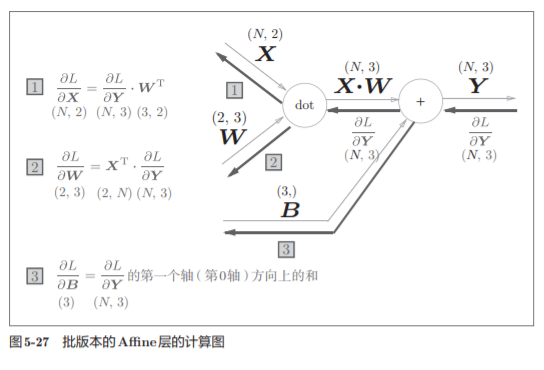
与刚刚不同，现在输入X的形状是(N, 2)。之后就和前面一样，在 计算图上进行单纯的矩阵计算。
由于正向传播时，偏置会被加到每一个数据（第1个、第2个……）上。反向传播时，各个数据的反向传播的值需要汇总为偏置的元素。
这个例子中，假定数据有2个（N = 2）。偏置的反向传播会对这2个数据 的导数按元素进行求和
这里使用了np.sum()对第0轴（以数据为单位的轴，axis=0）方向上的元素进行求和
实现考虑了输入数据为张量（四维数据）的情况，与这里介绍的稍有差别
5.6.3 Softmax-with-Loss 层
softmax函数，比如手写数字数字识别的时候：
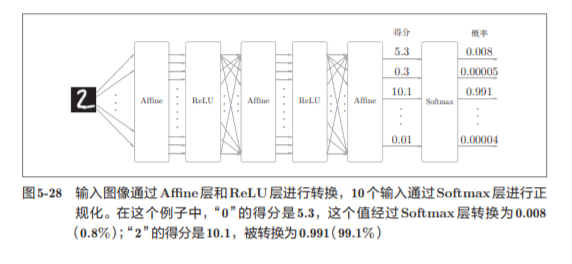
因为手写数字识别要进行10类分类，所以向Softmax层的输 入也有10个。
注意：
神经网络中进行的处理有推理（inference）和学习两个阶段。神经网 络的推理通常不使用 Softmax层。也就是说，当神经网络的推理只需要给出一个答案 的情况下，因为此时只对得分最大值感兴趣，所以不需要 Softmax层。 不过，神经网络的学习阶段则需要 Softmax层。
考虑到这里也包含作为损失函数的交叉熵误 差（cross entropy error），所以称为“Softmax-with-Loss层”。Softmax-withLoss层（Softmax函数和交叉熵误差）的计算图如图5-29所示。
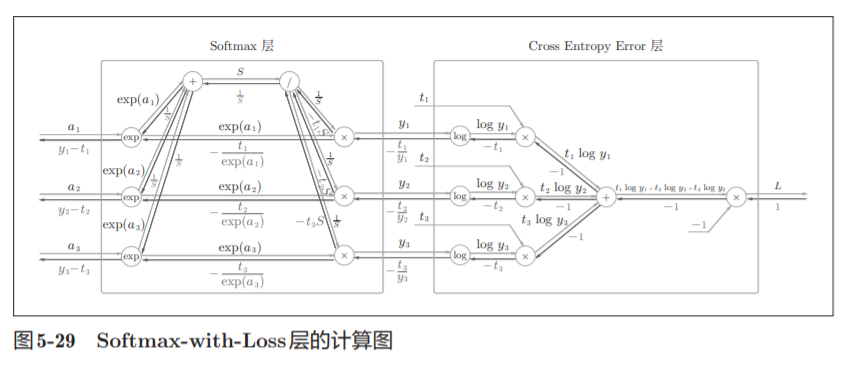
图5-29的计算图可以简化成图5-30
softmax函数记为Softmax层，交叉熵误差记为 Cross Entropy Error层。这里假设要进行3类分类，从前面的层接收3个输 入（得分）。如图5-30所示，Softmax层将输入（a1, a2, a3）正规化，输出（y1, y2, y3）。Cross Entropy Error层接收Softmax的输出（y1, y2, y3）和教师标签（t1, t2, t3），从这些数据中输出损失L。
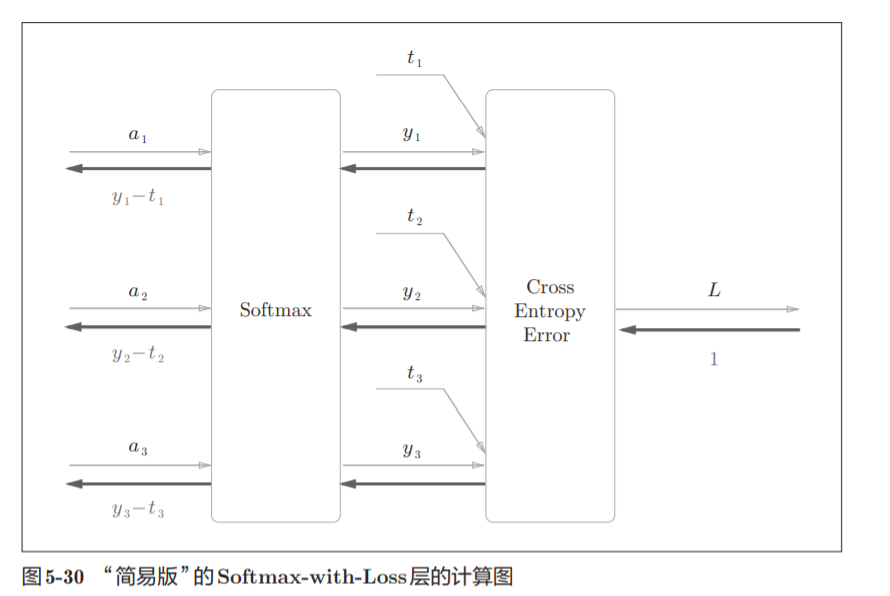
Softmax层的反向传播得到了 （y1 − t1, y2 − t2, y3 − t3）这样“漂亮”的结果。由于（y1, y2, y3）是Softmax层的 输出，（t1, t2, t3）是监督数据，所以（y1 − t1, y2 − t2, y3 − t3）是Softmax层的输 出和教师标签的差分。
神经网络学习的目的就是通过调整权重参数，使神经网络的输出（Softmax 的输出）接近教师标签。
必须将神经网络的输出与教师标签的误差高 效地传递给前面的层
具体例子：
如思考教师标签是（0, 1, 0），Softmax层 的输出是(0.3, 0.2, 0.5)的情形。因为正确解标签处的概率是0.2（20%），这个 时候的神经网络未能进行正确的识别。此时，Softmax层的反向传播传递的 是(0.3, −0.8, 0.5)这样一个大的误差。因为这个大的误差会向前面的层传播， 所以Softmax层前面的层会从这个大的误差中学习到“大”的内容。
注意：
使用“平 方和误差”作为“恒等函数”的损失函数，反向传播才能得到（y1 − t1, y2 − t2, y3 − t3）这样“漂亮”的结果。
再举一个例子，比如思考教师标签是(0, 1, 0)，Softmax层的输出是(0.01, 0.99, 0)的情形（这个神经网络识别得相当准确）。此时Softmax层的反向传播 传递的是(0.01, −0.01, 0)这样一个小的误差。这个小的误差也会向前面的层 传播，因为误差很小，所以Softmax层前面的层学到的内容也很“小”。
Softmax-with-Loss层的实现
请注意反向传播时，将要传播 的值除以批的大小（batch_size）后，传递给前面的层的是单个数据的误差
5.7 误差反向传播法的实现
5.7.1 神经网络学习的全貌图
神经网络的学习分为下面4个步骤
的误差反向传播法会在步骤2中出现
在上一节的实验，我们采用数值微分的方法进行实现，虽然简单，但是消耗时间过长。
5.7.2 对应误差反向传播法的神经网络的实现
这里我们要把2层神经网络实现为TwoLayerNet
与上一章非常类似
不同点主要在于这里使用了层。通过使用层，获得识别结果 的处理（predict()）和计算梯度的处理（gradient()）只需通过层之间的传递就能完成。
只截取不同的部分:
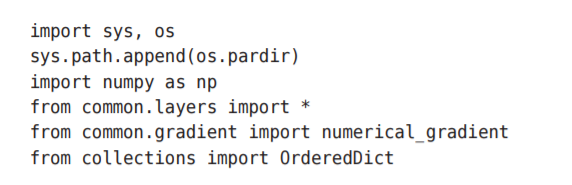
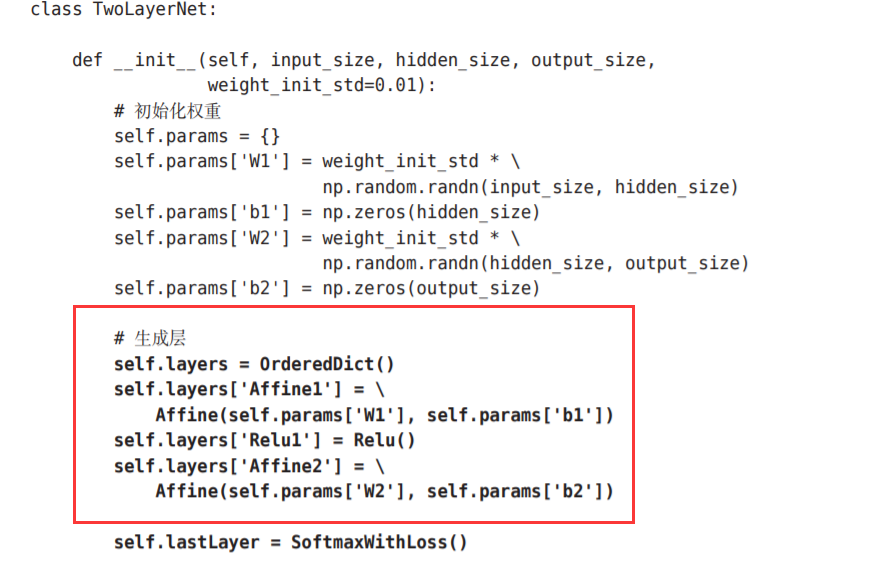
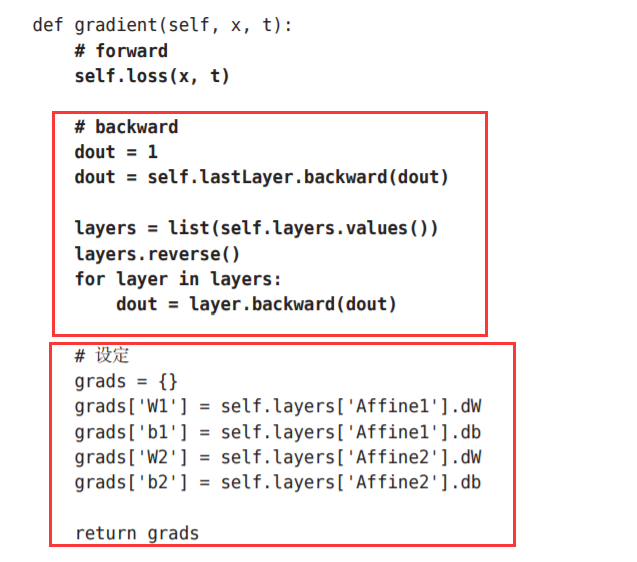
请注意这个实现中的粗体字代码部分，尤其是将神经网络的层保存为 OrderedDict这一点非常重要。OrderedDict是有序字典，“有序”是指它可以 记住向字典里添加元素的顺序。神经网络的正向传播只需按照添加元 素的顺序调用各层的forward()方法就可以完成处理，而反向传播只需要按 照相反的顺序调用各层即可。
因为Affine层和ReLU层的内部会正确处理正 向传播和反向传播，所以这里要做的事情仅仅是以正确的顺序连接各层，再 按顺序（或者逆序）调用各层
只需像组装乐高 积木那样添加必要的层就可构件一个较大的神经网络。
5.7.3 误差反向传播法的梯度确认
两种求梯度的方法：
一种是基于数值微分的方 法，另一种是解析性地求解数学式的方法。后一种方法通过使用误差反向传 播法，即使存在大量的参数，也可以高效地计算梯度。使用误差反向传播法求梯度。
在确认误差反向传播法的实现是否正确时，是需要用到数值微分的。
确认数值 微分求出的梯度结果和误差反向传播法求出的结果是否一致（严格地讲，是 非常相近）的操作称为梯度确认（gradient check）。
这里误差的计 算方法是求各个权重参数中对应元素的差的绝对值，并计算其平均值。运行 上面的代码后，会输出如下结果
比如，第1层的偏置的误差是9.7e-13（0.00000000000097）。这样一来， 我们就知道了通过误差反向传播法求出的梯度是正确的，误差反向传播法的 实现没有错误。
5.7.4 使用误差反向传播法的学习
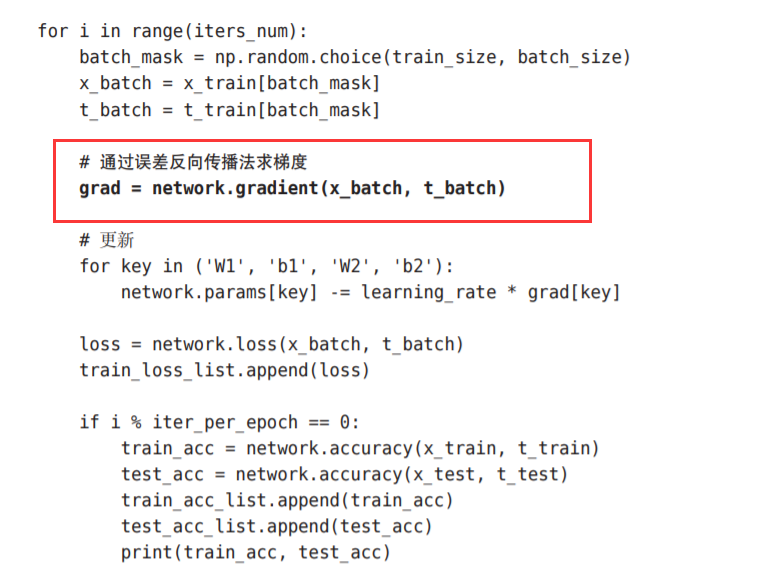
我们来看一下使用了误差反向传播法的神经网络的学习的实现。 和之前的实现相比，不同之处仅在于通过误差反向传播法求梯度这一点。
使用部分，与上一张的不同点只在于：
5.8 小结
使用计算图，介绍了神 经网络中的误差反向传播法，并以层为单位实现了神经网络中的处理，我们 学过的层有ReLU层、Softmax-with-Loss层、Affine层、Softmax层等，这 些层中实现了forward和backward方法，通过将数据正向和反向地传播，可 以高效地计算权重参数的梯度。通过使用层进行模块化，神经网络中可以自 由地组装层，轻松构建出自己喜欢的网络。
与学习相关的技巧
题涉及寻找最优权重 参数的最优化方法、权重参数的初始值、超参数的设定方法等
为了应对过拟合，本章还将介绍权值衰减、Dropout等正则化方法，对近年来众多研究中使用的Batch Normalization方法进行简单的介绍
6.1 参数的更新
神经网络的学习的目的是找到使损失函数的值尽可能小的参数。
前面我们通过的梯度（导数）作为了线索寻找最优参赛
随机梯度下降法（stochastic gradient descent）， 简称SGD
6.1.1 探险家的故事
简称瞎走，通过感觉找到
6.1.2 SGD
教学式：
式子中的←表示用右边的值更新左边的值。
参数更新：
后面我们马上会实现另一个最优化方法Momentum，optimizer = SGD()这一语句换成optimizer = Momentum()，就可以从SGD切 换为Momentum。
6.1.3 SGD的缺点
举个例子：
上式（6.2）表示的函数的梯度，如果用图表示，则如下：
虽然式 （6.2）的最小值在(x, y) = (0, 0)处，但是图6-2中的梯度在很多地方并没有指 向(0, 0)。
SGD的缺点是，如果函数的形状非均向（anisotropic），比如呈延伸状，搜索 的路径就会非常低效。
我们需要比单纯朝梯度方向前进的SGD更聪明的方法。SGD低效的根本原因是，梯度的方向并没有指向最小值的方向
将介绍Momentum、AdaGrad、Adam这3 种方法来取代SGD。
6.1.4 Momentum
这里新出现了一个变量v，对应物理上的速度。
式（6.3）表示了物体在梯度方向上受力，在这个力的作用下，物体的速度增 加这一物理法则。
实现代码：
和SGD相比，我们发现 “之”字形的“程度”减轻了。这是因为虽然x轴方向上受到的力非常小，但 是一直在同一方向上受力，所以朝同一个方向会有一定的加速。
6.1.5 AdaGrad
在关于学习率的有效技巧中，有一种被称为学习率衰减（learning rate decay）的方法，即随着学习的进行，使学习率逐渐减小。
在更新参数时，通过乘以1/根号h ，就可以调整学习的尺度。这意味着， 参数的元素中变动较大（被大幅更新）的元素的学习率将变小.
注意：
AdaGrad会记录过去所有梯度的平方和。学习越深入，更新 的幅度就越小，所以可以使用 RMSProp“指数移动平均”，呈指数函数式地减小 过去的梯度的尺度。
使用AdaGrad解决式（6.2）的最优化问题
由图6-6的结果可知，函数的取值高效地向着最小值移动。由于y轴方 向上的梯度较大，因此刚开始变动较大，但是后面会根据这个较大的变动按 比例进行调整，减小更新的步伐。因此，y轴方向上的更新程度被减弱，“之” 字形的变动程度有所衰减
6.1.6 Adam
Momentum参照小球在碗中滚动的物理规则进行移动，AdaGrad为参 数的每个元素适当地调整更新步伐。
于是乎两个结合在一起？这就是Adam方法的基本思路
通过组合前面两个方法的优点，有望 实现参数空间的高效搜索。具体的原理后面的时候可以看论文
注意：
Adam会设置 3个超参数。一个是学习率（论文中以α出现），另外两 个是一次momentum系数β1和二次momentum系数β2。根据论文， 标准的设定值是β1为 0.9，β2 为 0.999。设置了这些值后，大多数情 况下都能顺利运行。
6.1.7 使用哪种更新方法呢
非常遗憾，（目前）并不存在能在所有问题中都表现良好 的方法。这4种方法各有各的特点，都有各自擅长解决的问题和不擅长解决 的问题。
最近，很多研究人员和技术人员都喜欢用Adam。本书将主要使用 SGD或者Adam，读者可以根据自己的喜好多多尝试。
6.1.8 基于MNIST数据集的更新方法的比较
# coding: utf-8
import os
import sys
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.util import smooth_curve
from common.multi_layer_net import MultiLayerNet
from common.optimizer import *
# 0:读入MNIST数据==========
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000
# 1:进行实验的设置==========
optimizers = {}
optimizers['SGD'] = SGD()
optimizers['Momentum'] = Momentum()
optimizers['AdaGrad'] = AdaGrad()
optimizers['Adam'] = Adam()
#optimizers['RMSprop'] = RMSprop()
networks = {}
train_loss = {}
for key in optimizers.keys():
networks[key] = MultiLayerNet(
input_size=784, hidden_size_list=[100, 100, 100, 100],
output_size=10)
train_loss[key] = []
# 2:开始训练==========
for i in range(max_iterations):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
for key in optimizers.keys():
grads = networks[key].gradient(x_batch, t_batch)
optimizers[key].update(networks[key].params, grads)
loss = networks[key].loss(x_batch, t_batch)
train_loss[key].append(loss)
if i % 100 == 0:
print( "===========" + "iteration:" + str(i) + "===========")
for key in optimizers.keys():
loss = networks[key].loss(x_batch, t_batch)
print(key + ":" + str(loss))
# 3.绘制图形==========
markers = {"SGD": "o", "Momentum": "x", "AdaGrad": "s", "Adam": "D"}
x = np.arange(max_iterations)
for key in optimizers.keys():
plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 1)
plt.legend()
plt.show()
效果图：
这个实验以一个5层神经网络为对象，其中每层有100个神经元。激活 函数使用的是ReLU。
与SGD相比，其他3种方法学习得更快，而且 速度基本相同，仔细看的话，AdaGrad的学习进行得稍微快一点
6.2 权重的初始值
设定什么样的 权重初始值，经常关系到神经网络的学习能否成功
6.2.1 可以将权重初始值设为0吗
抑制过拟合、提高泛化能力的技巧——权值衰减（weight decay）。
在这之前的权重初始值都是像0.01 * np.random.randn(10, 100)这样，使用 由高斯分布生成的值乘以0.01后得到的值（标准差为0.01的高斯分布）
事实上，将权重初始值设为 0的话，将无法正确进行学习。为什么不能将权重初始值设为0呢？严格地说，为什么不能将权重初始 值设成一样的值呢？这是因为在误差反向传播法中，所有的权重值都会进行 相同的更新。
为了防止“权重均一化” （严格地讲，是为了瓦解权重的对称结构），必须随机生成初始值
6.2.2 隐藏层的激活值的分布
观察隐藏层的激活值 A （激活函数的输出数据）的分布，可以获得很多启 发。
实验的目的是通过改变这个尺度（标准差），观察激活值的分布如何变 化。现在，我们将保存在activations中的各层数据画成直方图
随着输出不断地靠近0（或者靠近1），它的导数的值逐渐接 近0。
因此，偏向0和1的数据分布会造成反向传播中梯度的值不断变小，最后消失。这个问题称为梯度消失（gradient vanishing）。层次加深的深度学习 中，梯度消失的问题可能会更加严重。
下面，将权重的标准差设为0.01，进行相同的实验。实验的代码只需要 把设定权重初始值的地方换成下面的代码即可。
使用标准差为0.01的高斯分布时，各层的激活值的分布 如图6-11所示
因为不像刚才的例子那样偏向0和1，所 以不会发生梯度消失的问题。但是，激活值的分布有所偏向，说明在表现力 上会有很大问题。为什么这么说呢？因为如果有多个神经元都输出几乎相同 的值，那它们就没有存在的意义了。
表现力受限问题、
为了使各层的激活值呈现出具有相同广度的分布，推导了合适的权重尺度。
前一层的节点数越多，要设定为目标节点的初始值的权重尺度就越小
使用Xavier初始值后的结果如图6-13所示。从这个结果可知，越是后 面的层，图像变得越歪斜，但是呈现了比之前更有广度的分布。
如果用tanh 函数（双曲线函数）代替sigmoid函数，这个稍微歪斜的问题就能得 到改善。
6.2.3 ReLU的权重初始值
Xavier初始值是以激活函数是线性函数为前提而推导出来的。因为 sigmoid函数和tanh函数左右对称，且中央附近可以视作线性函数，所以适 合使用Xavier初始值。但当激活函数使用ReLU时，一般推荐使用ReLU专 用的初始值，也就是Kaiming He等人推荐的初始值，也称为“He初始值“
因此：
总结一下：
当激活函数使用ReLU时，权重初始值使用He初始值；
当 激活函数为sigmoid或tanh等S型曲线函数时，初始值使用Xavier初始值。
这是目前的最佳实践。
6.2.4 基于MNIST数据集的权重初始值的比较
实现代码：
# coding: utf-8
import os
import sys
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.util import smooth_curve
from common.multi_layer_net import MultiLayerNet
from common.optimizer import SGD
# 0:读入MNIST数据==========
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000
# 1:进行实验的设置==========
weight_init_types = {'std=0.01': 0.01, 'Xavier': 'sigmoid', 'He': 'relu'}
optimizer = SGD(lr=0.01)
networks = {}
train_loss = {}
for key, weight_type in weight_init_types.items():
networks[key] = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100],
output_size=10, weight_init_std=weight_type)
train_loss[key] = []
# 2:开始训练==========
for i in range(max_iterations):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
for key in weight_init_types.keys():
grads = networks[key].gradient(x_batch, t_batch)
optimizer.update(networks[key].params, grads)
loss = networks[key].loss(x_batch, t_batch)
train_loss[key].append(loss)
if i % 100 == 0:
print("===========" + "iteration:" + str(i) + "===========")
for key in weight_init_types.keys():
loss = networks[key].loss(x_batch, t_batch)
print(key + ":" + str(loss))
# 3.绘制图形==========
markers = {'std=0.01': 'o', 'Xavier': 's', 'He': 'D'}
x = np.arange(max_iterations)
for key in weight_init_types.keys():
plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 2.5)
plt.legend()
plt.show()
基于MNIST数据集的权重初始值的比较：横轴是学习的迭代次数（iterations）， 纵轴是损失函数的值（loss）
从图6-15的结果可知，std = 0.01时完全无法进行学习。这和刚 才观察到的激活值的分布一样，是因为正向传播中传递的值很小（集中在0 附近的数据）。因此，逆向传播时求到的梯度也很小，权重几乎不进行更新。 相反，当权重初始值为Xavier初始值和He初始值时，学习进行得很顺利。 并且，我们发现He初始值时的学习进度更快一些。
综上：
权重初始值非常重要，关系到学习能否成功。
6.3 Batch Normalization
为了使各层拥有适当的广度，“强制性”地调整激活值的分布 会怎样呢？实际上，Batch Normalization为了使各层拥有适当的广度，“强制性”地调整激活值的分布 会怎样呢？实际上，Batch Normalization。
6.3.1 Batch Normalization 的算法
为什么Batch Norm这么惹人注目呢？因为Batch Norm有以下优点
可以使学习快速进行（可以增大学习率）。
- 不那么依赖初始值（对于初始值不用那么神经质）。
- 抑制过拟合（降低Dropout等的必要性）。
要向神经网络中插入对数据分布进行正规化的层，即Batch Normalization层（下文简称Batch Norm层）
Batch Norm，顾名思义，以进行学习时的mini-batch为单位，按minibatch进行正规化。
具体而言，就是进行使数据分布的均值为0、方差为1的 正规化
式（6.7）中的ε是一个微小值（比如，10e-7等），它是为了防止出现 除以0的情况。
式（6.7）所做的是将mini-batch的输入数据{x1, x2, ... , xm}变换为均值为0、方差为1的数据 ，非常简单。通过将这个处理插入到 激活函数的前面（或者后面）A，可以减小数据分布的偏向。
Batch Norm层会对正规化后的数据进行缩放和平移的变换
Batch Norm可以表示为图6-17
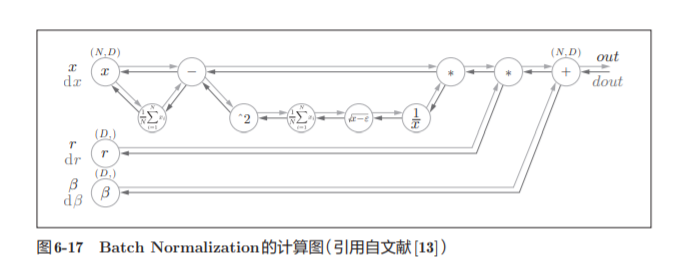
Batch Norm的反向传播的推导有些复杂，这里我们不进行介绍。
6.3.2 Batch Normalization的评估
实现代码：
实验效果图字体比较难调，所以用书本上的了
学习过程时间特别短：
综上，通过使用Batch Norm，可以推动学习的进行。并且，对权重初 始值变得健壮（“对初始值健壮”表示不那么依赖初始值）。Batch Norm具备 了如此优良的性质，一定能应用在更多场合中”
6.4 正则化
6.4.1 过拟合
发生过拟合的原因，主要有以下两个。
• 模型拥有大量参数、表现力强。
• 训练数据少
我们在实验过程中，先尝试这两个错误：
从 MNIST数据集原本的60000个训练数据中只选定300个，并且，为了增加网 络的复杂度，使用7层网络（每层有100个神经元，激活函数为ReLU）。
过了 100 个 epoch 左右后，用训练数据测量到的识别精度几乎都为 100%。但是，对于测试数据，离100%的识别精度还有较大的差距。如此大 的识别精度差距，是只拟合了训练数据的结果。从图中可知，模型对训练时 没有使用的一般数据（测试数据）拟合得不是很好。
6.4.2 权值衰减
权值衰减是一直以来经常被使用的一种抑制过拟合的方法。
对于所有权重，权值衰减方法都会为损失函数加上
因此，在求权 重梯度的计算中，要为之前的误差反向传播法的结果加上正则化项的导数λW
实现代码：
# coding: utf-8
import os
import sys
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.multi_layer_net import MultiLayerNet
from common.optimizer import SGD
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
# 为了再现过拟合，减少学习数据
x_train = x_train[:300]
t_train = t_train[:300]
# weight decay（权值衰减）的设定 =======================
#weight_decay_lambda = 0 # 不使用权值衰减的情况
weight_decay_lambda = 0.1
# ====================================================
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10,
weight_decay_lambda=weight_decay_lambda)
optimizer = SGD(lr=0.01)
max_epochs = 201
train_size = x_train.shape[0]
batch_size = 100
train_loss_list = []
train_acc_list = []
test_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
epoch_cnt = 0
for i in range(1000000000):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
grads = network.gradient(x_batch, t_batch)
optimizer.update(network.params, grads)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print("epoch:" + str(epoch_cnt) + ", train acc:" + str(train_acc) + ", test acc:" + str(test_acc))
epoch_cnt += 1
if epoch_cnt >= max_epochs:
break
# 3.绘制图形==========
markers = {'train': 'o', 'test': 's'}
x = np.arange(max_epochs)
plt.plot(x, train_acc_list, marker='o', label='train', markevery=10)
plt.plot(x, test_acc_list, marker='s', label='test', markevery=10)
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()结果：
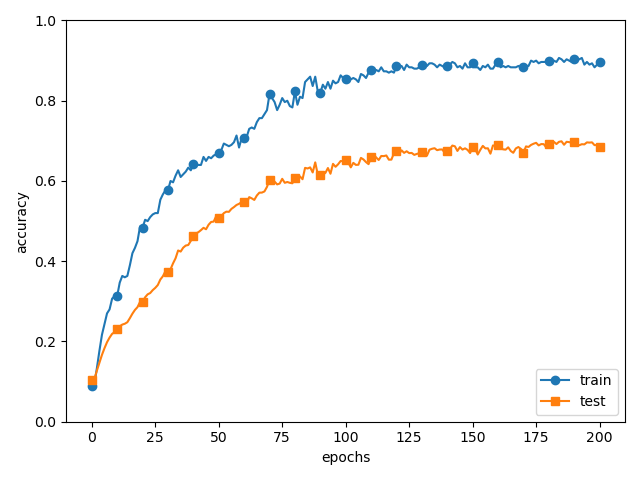
如图6-21所示，虽然训练数据的识别精度和测试数据的识别精度之间有 差距，但是与没有使用权值衰减的图6-20的结果相比，差距变小了
6.4.3 Dropout
如果网络的模型变得很复杂，我们经常会使用Dropout方法.
Dropout是一种在学习的过程中随机删除神经元的方法。训练时，每传递一次数据，就会随机选择要删除的神经元。
下面我们来实现Dropout。这里的实现重视易理解性。不过，因为训练 时如果进行恰当的计算的话，正向传播时单纯地传递数据就可以了（不用乘 以删除比例），所以深度学习的框架中进行了这样的实现。关于高效的实现， 可以参考Chainer中实现的Dropou
这里的要点是，每次正向传播时，self.mask中都会以False的形式保 存要删除的神经元。self.mask会随机生成和x形状相同的数组，并将值比 dropout_ratio大的元素设为True。反向传播时的行为和ReLU相同
我们使用MNIST数据集进行验证，以确认Dropout的效果。源代 码在ch06/overfit_dropout.py中。另外，源代码中使用了Trainer类来简化实现
# coding: utf-8
import os
import sys
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.multi_layer_net_extend import MultiLayerNetExtend
from common.trainer import Trainer
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
# 为了再现过拟合，减少学习数据
x_train = x_train[:300]
t_train = t_train[:300]
# 设定是否使用Dropuout，以及比例 ========================
use_dropout = True # 不使用Dropout的情况下为False
dropout_ratio = 0.2
# ====================================================
#用Dropout的情况下
network = MultiLayerNetExtend(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100],
output_size=10, use_dropout=use_dropout, dropout_ration=dropout_ratio)
trainer = Trainer(network, x_train, t_train, x_test, t_test,
epochs=301, mini_batch_size=100,
optimizer='sgd', optimizer_param={'lr': 0.01}, verbose=True)
trainer.train()
train_acc_list, test_acc_list = trainer.train_acc_list, trainer.test_acc_list
# 绘制图形==========
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, marker='o', label='train', markevery=10)
plt.plot(x, test_acc_list, marker='s', label='test', markevery=10)
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()结果：
图6-23中，通过使用Dropout，训练数据和测试数据的识别精度的差距 变小了。
6.5 超参数的验证
这里所说的超参数是指，比如各层的神经元数量、batch大小、参 数更新时的学习率或权值衰减等
6.5.1 验证数据
为什么不能用测试数据评估超参数的性能呢？这是因为如果使用测试数 据调整超参数，超参数的值会对测试数据发生过拟合。
用于调整超参 数的数据，一般称为验证数据（validation data）。我们使用这个验证数据来 评估超参数的好坏。
与吴恩达的三部分数据划分一致。有的会事先分成训练数据、验证数据、测试数据三 部分，有的只分成训练数据和测试数据两部分。
6.5.2 超参数的最优化
所谓逐渐缩小范围，是指一开始先大致设定一个范围，从这个范围中随机选 出一个超参数（采样），用这个采样到的值进行识别精度的评估
超参数的范围只要“大致地指定”就可以了。所谓“大致地指定”，是指 像0.001（10^−3 ）到1000（10^3 ）这样，以“10的阶乘”的尺度指定范围（也表述 为“用对数尺度（log scale）指定”）。
超参数的最优化的内容，简单归纳一下，如下所示。
这里介绍的超参数的最优化方法是实践性的方法。... 人为调参
6.5.3 超参数最优化的实现
如前所述，通过从 0.001（10^−3 ）到 1000（10^3)
这样的对数尺度的范围 中随机采样进行超参数的验证。
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.multi_layer_net import MultiLayerNet
from common.util import shuffle_dataset
from common.trainer import Trainer
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
# 为了实现高速化，减少训练数据
x_train = x_train[:500]
t_train = t_train[:500]
# 分割验证数据
validation_rate = 0.20
validation_num = int(x_train.shape[0] * validation_rate)
x_train, t_train = shuffle_dataset(x_train, t_train)
x_val = x_train[:validation_num]
t_val = t_train[:validation_num]
x_train = x_train[validation_num:]
t_train = t_train[validation_num:]
def __train(lr, weight_decay, epocs=50):
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100],
output_size=10, weight_decay_lambda=weight_decay)
trainer = Trainer(network, x_train, t_train, x_val, t_val,
epochs=epocs, mini_batch_size=100,
optimizer='sgd', optimizer_param={'lr': lr}, verbose=False)
trainer.train()
return trainer.test_acc_list, trainer.train_acc_list
# 超参数的随机搜索======================================
optimization_trial = 100
results_val = {}
results_train = {}
for _ in range(optimization_trial):
# 指定搜索的超参数的范围===============
# 0.001（10^−3 ）到 1000（10^3) 对数尺度的范围
# 中随机采样进行超参数的验证
# 权值衰减系数的初始范围为10−8 到10−4
# 学习率的初始范围为10^−6到10^−2
weight_decay = 10 ** np.random.uniform(-8, -4)
lr = 10 ** np.random.uniform(-6, -2)
# ================================================
val_acc_list, train_acc_list = __train(lr, weight_decay)
print("val acc:" + str(val_acc_list[-1]) + " | lr:" + str(lr) + ", weight decay:" + str(weight_decay))
key = "lr:" + str(lr) + ", weight decay:" + str(weight_decay)
results_val[key] = val_acc_list
results_train[key] = train_acc_list
# 绘制图形========================================================
print("=========== Hyper-Parameter Optimization Result ===========")
graph_draw_num = 20
col_num = 5
row_num = int(np.ceil(graph_draw_num / col_num))
i = 0
for key, val_acc_list in sorted(results_val.items(), key=lambda x:x[1][-1], reverse=True):
print("Best-" + str(i+1) + "(val acc:" + str(val_acc_list[-1]) + ") | " + key)
plt.subplot(row_num, col_num, i+1)
plt.title("Best-" + str(i+1))
plt.ylim(0.0, 1.0)
if i % 5: plt.yticks([])
plt.xticks([])
x = np.arange(len(val_acc_list))
plt.plot(x, val_acc_list)
plt.plot(x, results_train[key], "--")
i += 1
if i >= graph_draw_num:
break
plt.show()
这样就能缩小到合适的超参数的存在范围，然后在某个阶段，选择一个最终 的超参数的值
6.6 小结
本章我们介绍了神经网络的学习中的几个重要技巧。
参数的更新方法、 权重初始值的赋值方法、Batch Normalization、Dropout等，这些都是现代 神经网络中不可或缺的技术。另外，这里介绍的技巧，在最先进的深度学习 中也被频繁使用。
吴恩达的视屏看完后看这个真的会有不一样的收获。
卷积神经网络（Convolutional Neural Network，CNN）
7.1 整体结构
之前介绍的神经网络中，相邻层的所有神经元之间都有连接，这称为全连接（fully-connected）。
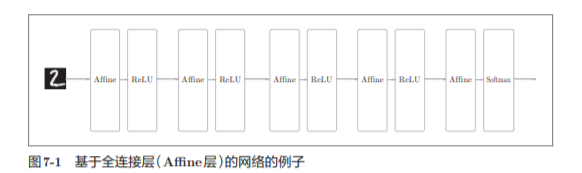
CNN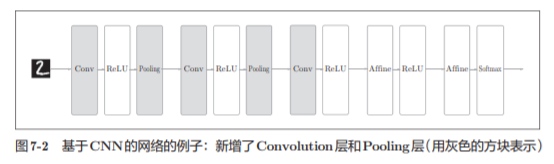
7.2 卷积层
全连接层存在什么问题呢？那就是数据的形状被“忽视”了。比如，输 入数据是图像时，图像通常是高、长、通道方向上的3维形状。
CNN 中，有时将卷积层的输入输出数据称为特征图（feature map）。其中，卷积层的输入数据称为输入特征图（input feature map），输出 数据称为输出特征图（output feature map）。
7.2.2 卷积运算
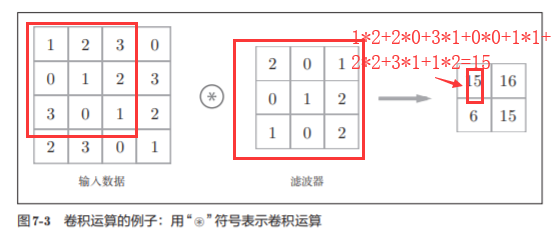
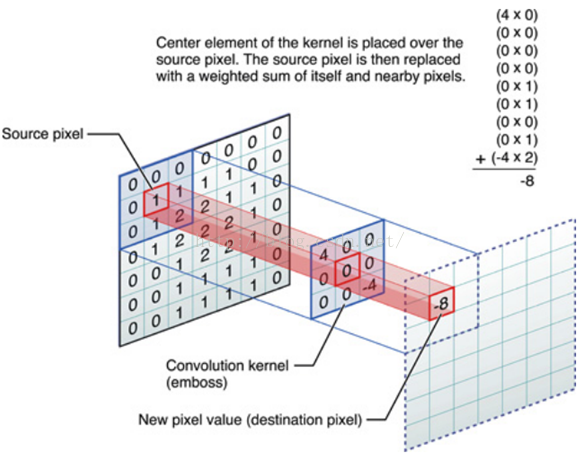
如图7-4所示，将各个位置上滤 波器的元素和输入的对应元素相乘，然后再求和（有时将这个计算称为乘积累加运算）。
参考论文：
具体的计算过程：
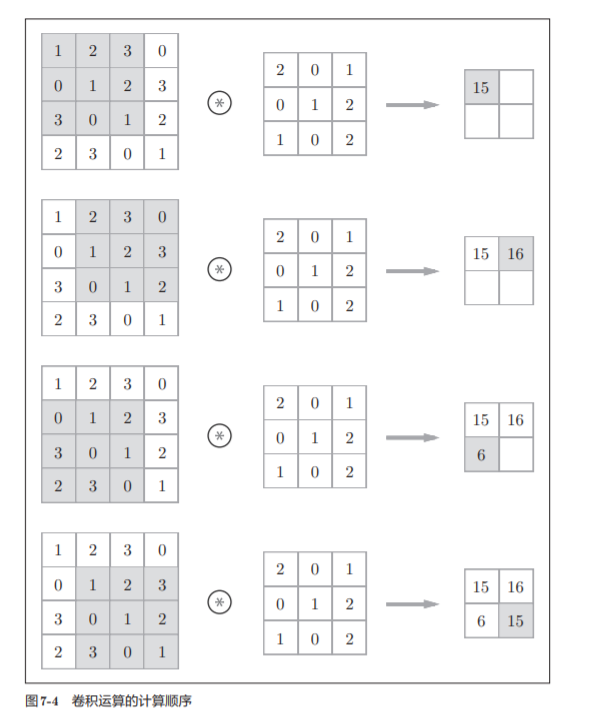
CNN同样可以加偏置
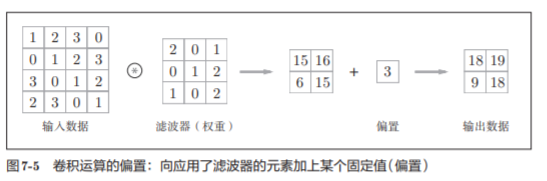
7.2.3 填充
在进行卷积层的处理之前，有时要向输入数据的周围填入固定的数据（比 如0等），这称为填充（padding）
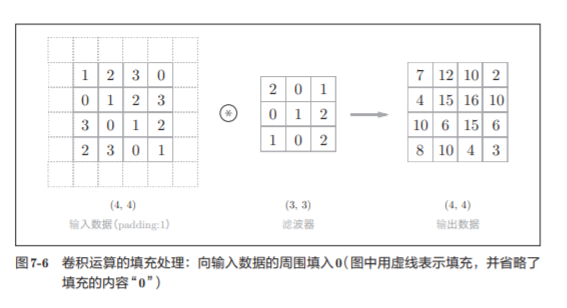
这个例 子中将填充设成了1，不过填充的值也可以设置成2、3等任意的整数。
在图7-5 的例子中，如果将填充设为2，则输入数据的大小变为(8, 8)；如果将填充设 为3，则大小变为(10, 10)。
使用填充主要是为了调整输出的大小
7.2.4 步幅
应用滤波器的位置间隔称为步幅（stride）
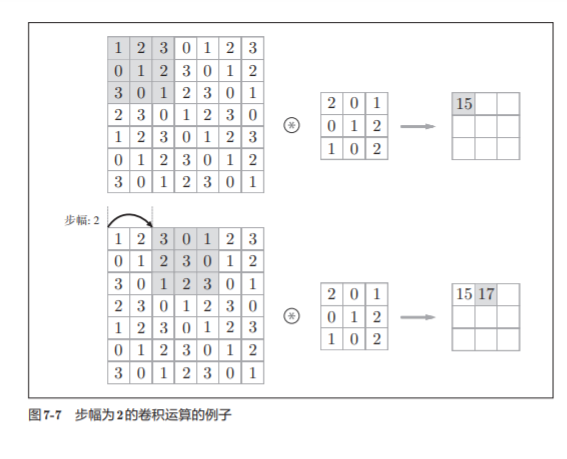
假设输入大小为(H, W)，滤波器大小为(FH, FW)，输出大小为 (OH, OW)，填充为P，步幅为S。此时，输出大小可通过式(7.1)进行计算
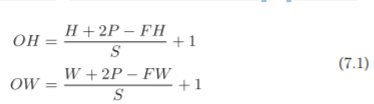
利用公式计算：
既然是除法，就要注意是否可以除尽，如果不能除尽，则进行报错等措施。
根据深度学习 的框架的不同，当值无法除尽时，有时会向最接近的整数四舍五入，不进行 报错而继续运行
7.2.5 3维数据的卷积运算
之前的卷积运算的例子都是以有高、长方向的2维形状为对象的
除了高、长方向之外，还需要处理通道方向。
图7-8是卷积运算的例子，图7-9是计算顺序。这里以3通道的数据为例， 展示了卷积运算的结果。
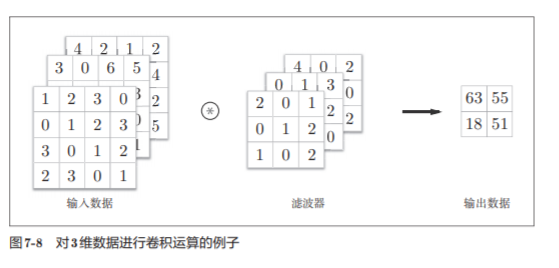
输入数据和滤波器的通道数一致，均为3
通道数只能设定为和输入数据的通道数相同的值
7.2.6 结合方块思考
把3维数据表示为多维数组 时，书写顺序为（channel, height, width）。比如，通道数为C、高度为H、 长度为W的数据的形状可以写成（C, H, W）。通道数为C、滤波器高度为FH（Filter Height）、长度为FW（Filter Width）时，可以写成（C, FH, FW）
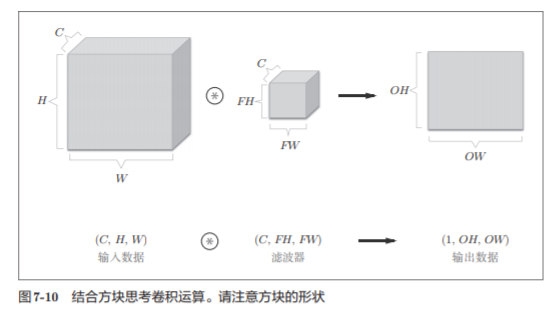
在这个例子中，数据输出是1张特征图。所谓1张特征图，换句话说， 就是通道数为1的特征图。那么，如果要在通道方向上也拥有多个卷积运算的输出，该怎么做呢？
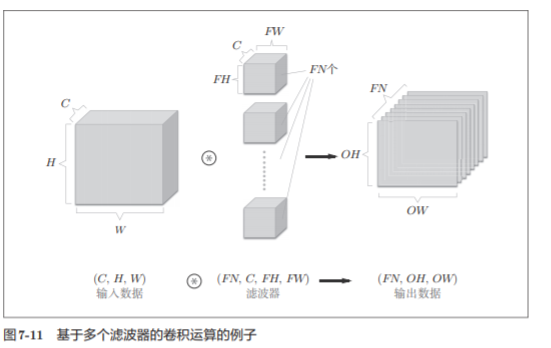
如图 7-11 所示，关于卷积运算的滤波器，也必须考虑滤波器的数量。因此，作为4维数据，滤波器的权重数据要按(output_channel, input_ channel, height, width)的顺序书写。
比如，通道数为3、大小为5 × 5的滤 波器有20个时，可以写成(20, 3, 5, 5)。
格式非常重要
在图7-11的例子中，如果进 一步追加偏置的加法运算处理，则结果如下面的图7-12所示。
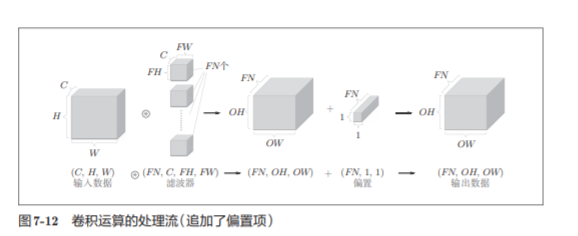
7.2.7 批处理
批处理将N次 的处理汇总成了1次进行
7.3 池化层
池化是缩小高、长方向上的空间的运算。
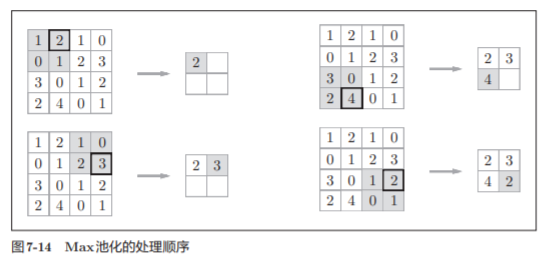
池化的窗口大小会 和步幅设定成相同的值
池化层的特征
- 通道数不发生变化
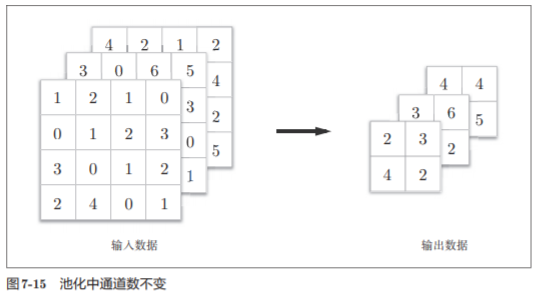
- 对微小的位置变化具有鲁棒性（健壮）
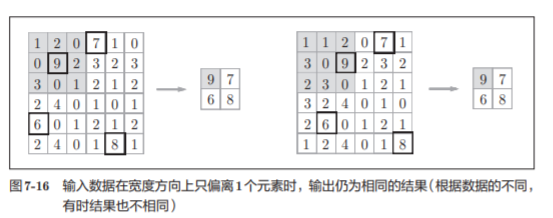
7.4 卷积层和池化层的实现
7.4.1 4维数组
CNN中各层间传递的数据是4维数据。
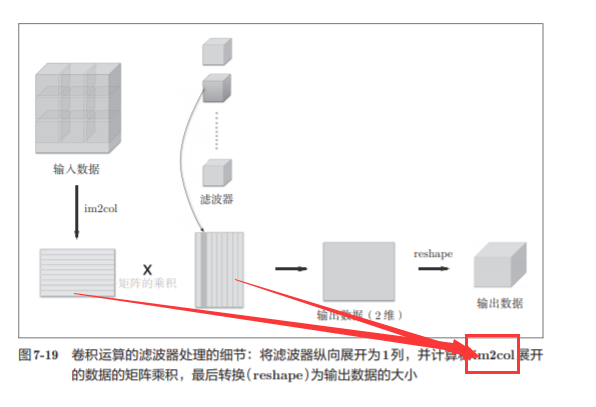
7.4.2 基于 im2col的展开
im2col这个名称是“image to column”的缩写，翻译过来就是“从图像到矩阵”的意思。
我们不使用for语句，而是使 用im2col这个便利的函数进行简单的实现。
im2col是一个函数，将输入数据展开以适合滤波器（权重）。如图7-17所示， 对3维的输入数据应用im2col后，数据转换为2维矩阵（正确地讲，是把包含批数量的4维数据转换成了2维数据）。
im2col会把输入数据展开以适合滤波器（权重）。具体地说，如图7-18所示， 对于输入数据，将应用滤波器的区域（3维方块）横向展开为1列。im2col会 在所有应用滤波器的地方进行这个展开处理。
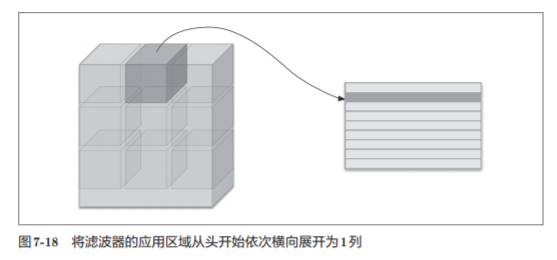
注意：
- 为了便于观察，将步幅设置得很大，以使滤波器的应用区域不重叠。
- 实际的卷积运算中，滤波器的应用区域几乎都是重叠的。
使用im2col展开后，展开后的元素个数会多于原方块的元素个数。
因此，使用im2col的实现存在比普通的实现消耗更多内存的缺点。
然而大的矩阵运算是可以被优化的
7.4.3 卷积层的实现
Im2col会考虑滤波器大小、步幅、填充，将输入数据展开为2纬数组
利用前面提及到的公式
下面是卷积层实现类：
其中transpose函数的可以基于Numpy调换索引对应元素的位置：
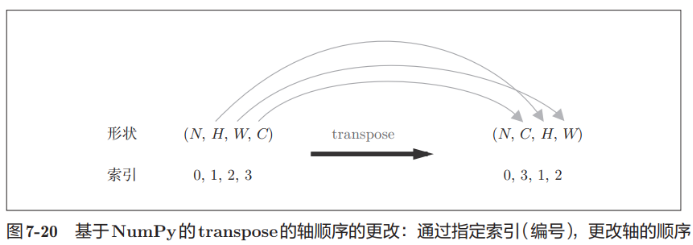
注：
（权重）、偏置、步幅、填充作为参数接收。
滤波器是 (FN, C, FH, FW)的 4 维形状。另外，FN、C、FH、FW分别是 Filter Number（滤波器数量）、Channel、Filter Height、Filter Width的缩写
7.4.4 池化层的实现
池化层可以单独按通道展开，如下图所示：
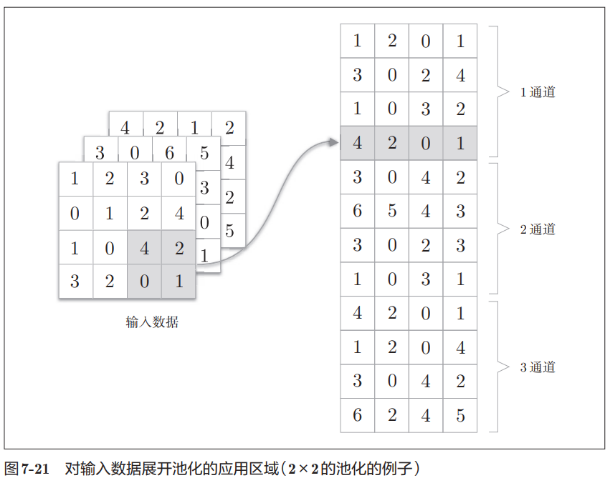
展开后根据矩阵的行选择需要的函数进行取值即可，如这里使用的是max函数，取完值之后在用reshape函数进行重构维度即可，如图所示：
池化层实现类：
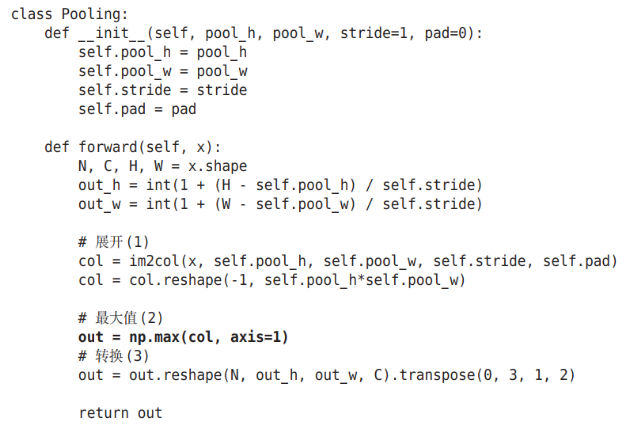
总结：实现池化层的3个步骤：
1. 展开输入数据
2.求各行的最大值
3.转换为合适的输出大小
7.5 CNN的实现
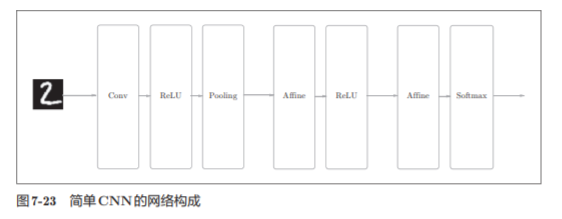
我们已经实现了卷积层和池化层，现在来组合这些层。
搭建进行手写数字识别的CNN。这里要实现如图所示的CNN
SimpleConvNet的初始化（__init__）
实现代码：
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
import pickle
import numpy as np
from collections import OrderedDict
from common.layers import *
from common.gradient import numerical_gradient
class SimpleConvNet:
"""简单的ConvNet
conv - relu - pool - affine - relu - affine - softmax
Parameters
----------
input_size : 输入大小（MNIST的情况下为784）
hidden_size_list : 隐藏层的神经元数量的列表（e.g. [100, 100, 100]）
output_size : 输出大小（MNIST的情况下为10）
activation : 'relu' or 'sigmoid'
weight_init_std : 指定权重的标准差（e.g. 0.01）
指定'relu'或'he'的情况下设定“He的初始值”
指定'sigmoid'或'xavier'的情况下设定“Xavier的初始值”
"""
def __init__(self, input_dim=(1, 28, 28),
conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1},
hidden_size=100, output_size=10, weight_init_std=0.01):
filter_num = conv_param['filter_num']
filter_size = conv_param['filter_size']
filter_pad = conv_param['pad']
filter_stride = conv_param['stride']
input_size = input_dim[1]
conv_output_size = (input_size - filter_size + 2*filter_pad) / filter_stride + 1
pool_output_size = int(filter_num * (conv_output_size/2) * (conv_output_size/2))
# 初始化权重
self.params = {}
self.params['W1'] = weight_init_std * \
np.random.randn(filter_num, input_dim[0], filter_size, filter_size)
self.params['b1'] = np.zeros(filter_num)
self.params['W2'] = weight_init_std * \
np.random.randn(pool_output_size, hidden_size)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = weight_init_std * \
np.random.randn(hidden_size, output_size)
self.params['b3'] = np.zeros(output_size)
# 生成层
self.layers = OrderedDict()
self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'],
conv_param['stride'], conv_param['pad'])
self.layers['Relu1'] = Relu()
self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2)
self.layers['Affine1'] = Affine(self.params['W2'], self.params['b2'])
self.layers['Relu2'] = Relu()
self.layers['Affine2'] = Affine(self.params['W3'], self.params['b3'])
# 只有SoftmaxWithLoss层被添加到别的变量lastLayer中
self.last_layer = SoftmaxWithLoss()
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, t):
"""求损失函数
参数x是输入数据、t是教师标签
"""
y = self.predict(x)
return self.last_layer.forward(y, t)
def accuracy(self, x, t, batch_size=100):
if t.ndim != 1 : t = np.argmax(t, axis=1)
acc = 0.0
for i in range(int(x.shape[0] / batch_size)):
tx = x[i*batch_size:(i+1)*batch_size]
tt = t[i*batch_size:(i+1)*batch_size]
y = self.predict(tx)
y = np.argmax(y, axis=1)
acc += np.sum(y == tt)
return acc / x.shape[0]
def numerical_gradient(self, x, t):
"""求梯度（数值微分）
Parameters
----------
x : 输入数据
t : 教师标签
Returns
-------
具有各层的梯度的字典变量
grads['W1']、grads['W2']、...是各层的权重
grads['b1']、grads['b2']、...是各层的偏置
"""
loss_w = lambda w: self.loss(x, t)
grads = {}
for idx in (1, 2, 3):
grads['W' + str(idx)] = numerical_gradient(loss_w, self.params['W' + str(idx)])
grads['b' + str(idx)] = numerical_gradient(loss_w, self.params['b' + str(idx)])
return grads
def gradient(self, x, t):
"""求梯度（误差反向传播法）
Parameters
----------
x : 输入数据
t : 教师标签
Returns
-------
具有各层的梯度的字典变量
grads['W1']、grads['W2']、...是各层的权重
grads['b1']、grads['b2']、...是各层的偏置
"""
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
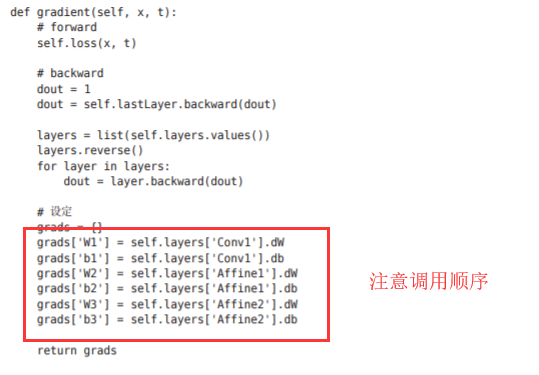
# 设定
grads = {}
grads['W1'], grads['b1'] = self.layers['Conv1'].dW, self.layers['Conv1'].db
grads['W2'], grads['b2'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
grads['W3'], grads['b3'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
return grads
def save_params(self, file_name="params.pkl"):
params = {}
for key, val in self.params.items():
params[key] = val
with open(file_name, 'wb') as f:
pickle.dump(params, f)
def load_params(self, file_name="params.pkl"):
with open(file_name, 'rb') as f:
params = pickle.load(f)
for key, val in params.items():
self.params[key] = val
for i, key in enumerate(['Conv1', 'Affine1', 'Affine2']):
self.layers[key].W = self.params['W' + str(i+1)]
self.layers[key].b = self.params['b' + str(i+1)]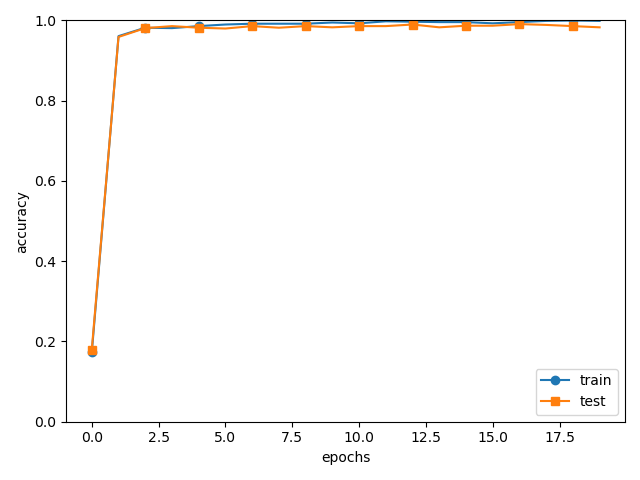
test acc:0.9892
注意：
将第1层的卷积层的权重设为关键字W1，偏置设为关键字b1。同样，分别用关键字W2、b2和关键字W3、b3 来保存第2个和第3个全连接层的权重和偏置。
预测与损失函数
是基于误差反向传播法求梯度
实现部分与前面的一样：
# 读入数据
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=False)
# 处理花费时间较长的情况下减少数据
#x_train, t_train = x_train[:5000], t_train[:5000]
#x_test, t_test = x_test[:1000], t_test[:1000]
max_epochs = 20
network = SimpleConvNet(input_dim=(1,28,28),
conv_param = {'filter_num': 30, 'filter_size': 5, 'pad': 0, 'stride': 1},
hidden_size=100, output_size=10, weight_init_std=0.01)
trainer = Trainer(network, x_train, t_train, x_test, t_test,
epochs=max_epochs, mini_batch_size=100,
optimizer='Adam', optimizer_param={'lr': 0.001},
evaluate_sample_num_per_epoch=1000)
trainer.train()
# 保存参数
network.save_params("params.pkl")
print("Saved Network Parameters!")7.6 CNN的可视化
7.6.1 第 1层权重的可视化
我们将卷积层（第1层）的滤波器显示为图像
学习前的滤波器是随机进行初始化的，所以在黑白的浓淡上 没有规律可循，但学习后的滤波器变成了有规律的图像
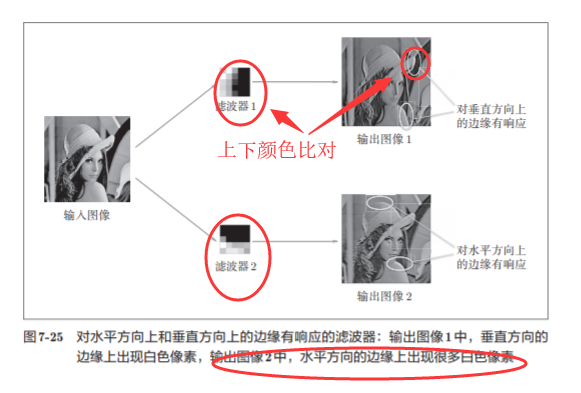
7.6.2 基于分层结构的信息提取
随着层次加深，提取的信息（正确地讲，是反映强烈的神经元）也越来越抽象
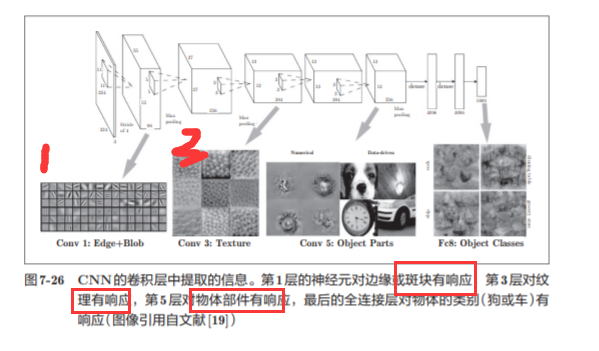
7.7 具有代表性的 CNN
7.7.1 LeNet
它有连续的卷积层和池化层（正确地讲，是只“抽选元素”的子采样层），最后经全连接层输出结果。
“现在的CNN”相比，LeNet有几个不同点:
-
第一个不同点在于激活函数。LeNet中使用sigmoid函数，而现在的CNN中主要使用ReLU函数。
-
原始的LeNet中使用子采样（subsampling）缩小中间数据的大小，而 现在的CNN中Max池化是主流
LeNet与现在的CNN虽然有些许不同，但差别并不是那么大.古老的东西
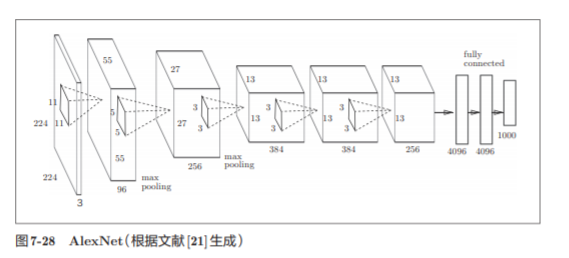
7.7.2 AlexNet
它的网络结构和LeNet基本上没有什么不同，AlexNet叠有多个卷积层和池化层，最后经由全连接层输出结果。
AlexNet和LeNet没有大的不同，但有以下几点差异
小结
- CNN在此前的全连接层的网络中新增了卷积层和池化层。
- 使用im2col函数可以简单、高效地实现卷积层和池化层。
- 通过CNN的可视化，可知随着层次变深，提取的信息愈加高级。
- LeNet和AlexNet是CNN的代表性网络。
- 在深度学习的发展中，大数据和GPU做出了很大的贡献。
卷积-ReLu函数-池化层-卷积-ReLu函数-池化层-卷积-ReLu函数-Affine-ReLu-Affine-Softmax