1.2）深度学习笔记------神经网络的编程基础

1）Binary Classification

2）Logistic Regression

3）Logistic Regression Cost Function

4）Gradient Descent

5）Logistic Regression Gradient Descent（重点）

6）Gradient Descent on m Examples

7）Vectorization Logistic Regression's Gradient（重点）

8）Broadcasting in Python

9）A note on python or numpy vectors

10）Explanation of logistic regression cost function（选修）

以下笔记是吴恩达老师深度学习课程第一门课第二周的的学习笔记：Basics of Neural Network programming。笔记参考了黄海广博士的内容，在此表示感谢。

1）Binary Classification

这一节，我们学习本课程中用到的符号：

：表示一个维数据，为输入数据，维度为

：表示输出结果，取值为

$(x^{(i)},y^{(i)})$ ：表示第i组数据；

$X=[x^{(1)},x^{(2)},...,x^{(m)}]$ ：表示所有的训练数据集的输入值，放在一个的矩阵中；

$Y=[y^{(1)},y^{(2)},...,y^{(m)}]$ ：对应表示所有悬链数据的输出值，维度为；

2）Logistic Regression

之前在吴恩达老师的机器学习课程中已经介绍过了，这里主要是复习一下逻辑函数。

Logistic 回归是一个用于二元分类的算法。

Logistic 回归中使用的参数如下：

输入的特征向量： $x \in R^{n_x}$ ，其中 ${n_x}$ 是特征数量；

用于训练的标签： $y \in 0,1$

权重： $w \in R^{n_x}$

偏置： $b \in R$

输出： $\hat{y}=\sigma(w^Tx+b)$

Sigmoid 函数： $s = \sigma(w^Tx+b) = \sigma(z) = \frac{1}{1+e^{-z}}$

预测值为表示1的概率，故引入 Sigmoid 函数。从下图可看出，Sigmoid 函数的值域为 [0, 1]。

3）Logistic Regression Cost Function

损失函数（loss function）用于衡量预测结果与真实值之间的误差。最简单的损失函数定义方式为平方差损失：

$L(\hat{y},y) = \frac{1}{2}(\hat{y}-y)^2$

但是，对于logistic regression 来说，一般不适用平方差来作为Loss Function，这是因为上面的平方差损失函数对于逻辑回归问题一般是非凸函数（non-convex），其在使用梯度下降算法的时候，容易得到局部最优解，而不是全局最优解。因此要选择凸函数。

逻辑回归的Loss Function：

$L(\hat{y},y) = -(y\log\hat{y})-(1-y)\log(1-\hat{y})$

损失函数是在单个训练样本中定义的，它衡量了在单个训练样本上的表现。而代价函数（cost function，或者称作成本函数）衡量的是在全体训练样本上的表现，即衡量参数 w 和 b 的效果。

$$$J(w,b) = \frac{1}{m}\sum_{i=1}^mL(\hat{y}^{(i)},y^{(i)})$

4）Gradient Descent

函数的梯度（gradient）指出了函数的最陡增长方向。即是说，按梯度的方向走，函数增长得就越快。那么按梯度的负方向走，函数值自然就降低得最快了。

模型的训练目标即是寻找合适的 w 与 b 以最小化代价函数值。简单起见我们先假设 w 与 b 都是一维实数，那么可以得到如下的 J 关于 w 与 b 的图：

可以看到，成本函数 J 是一个凸函数，与非凸函数的区别在于其不含有多个局部最低点；选择这样的代价函数就保证了无论我们如何初始化模型参数，都能够寻找到合适的最优解。

每次迭代更新的修正表达式：

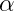
$w:=w-\alpha\frac{\partial{J(w,b)}}{\partial{w}}$

$b:=b-\alpha\frac{\partial{J(w,b)}}{\partial{b}}$

其中， $\alpha$ 表示学习速率，即每次更新参数的步伐长度。

5）Logistic Regression Gradient Descent（重点）

本节笔记之前吴恩达老师课程介绍了导数，计算图，使用计算图的例子，考虑到这部分内容不是很难，故没有记载，需要的同学可以回看吴恩达老师的课程视频或黄海广博士的笔记。

这一节详细介绍了逻辑回归中梯度的计算和参数的更新，这部分掌握了对后面神经网络的学习很有帮助。

对单个样本而言，逻辑回归Loss function表达式：

z=w^Tx+b

$\hat{y}=a=\sigma(z)$

L(a,y)=-(ylog(a)+(1-y)log(1-a))

假设输入的特征向量维度为 2，即输入参数共有 x1, w1, x2, w2, b 这五个。可以推导出如下的计算图：

首先反向求出 L 对于 a 对 z 的导数：

$da=\frac{dL(a,y)}{da}=-\frac{y}{a}+\frac{1-y}{1-a}$

$dz=\frac{dL}{dz}=\frac{dL}{da}\frac{da}{dz}=a-y$

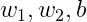
再对 w_1,w_2,b 进行求导：

dw_1=x_1dz=x_1(a-y)

dw_2=x_2dz=x_2(a-y)

db=dz=(a-y)

梯度下降法更新参数可得：

$w_1:=w_1-\alpha{dw_1}$

$w_2:=w_2-\alpha{dw_2}$

$b:=b-\alpha{db}$

6）Gradient Descent on m Examples

对m个样本来说，其Cost function表达式如下：

$z^{(i)}=w^Tx^{(i)}+b$

$\hat{y}^{(i)}=a^{(i)}=\sigma(z^{(i)})$

$J(w,b)=\frac{1}{m}\sum^m_{i=1}L(a^{(i)},y^{(i)})$

Cost function 关于w和b的偏导数可以写成所有样本点偏导数和的平均形式：

$dw_1=\frac{\partial J(w,b)}{\partial{w_1}}=\frac{1}{m}\sum^m_{i=1}\frac{\partial L(a^{(i)},y^{(i)})}{\partial{w_1}}=\frac{1}{m}\sum_{i=1}^{m}x_1^{(i)}(a^{(i)}-y^{(i)})$

$dw_2=\frac{\partial J(w,b)}{\partial{w_2}}=\frac{1}{m}\sum^m_{i=1}\frac{\partial L(a^{(i)},y^{(i)})}{\partial{w_2}}=\frac{1}{m}\sum_{i=1}^{m}x_2^{(i)}(a^{(i)}-y^{(i)})$

$db=\frac{\partial J(w,b)}{\partial{b}}=\frac{1}{m}\sum^m_{i=1}\frac{\partial L(a^{(i)},y^{(i)})}{\partial{b}}=\frac{1}{m}\sum_{i=1}^{m}(a^{(i)}-y^{(i)})$

完整的 Logistic 回归中某次训练的流程如下，这里仅假设特征向量的维度为 2：

然后对参数进行迭代。

上述过程在计算时有一个缺点：你需要编写两个 for 循环。第一个 for 循环遍历 m 个样本，而第二个 for 循环遍历所有特征。如果有大量特征，在代码中显式使用 for 循环会使算法很低效。向量化可以用于解决显式使用 for 循环的问题。

7）Vectorization Logistic Regression's Gradient（重点）

在深度学习的算法中，我们通常拥有大量的数据，在程序的编写过程中，应该尽最大可能的少使用loop循环语句，利用python可以实现矩阵运算，进而来提高程序的运行速度，避免for循环的使用。

在 Logistic 回归中，需要计算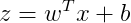 $$z=w^Tx+b$$ 如果是非向量化的循环方式操作，代码可能如下：

z = 0;
for i in range(n_x):
    z += w[i] * x[i]
z += b

而如果是向量化的操作，代码则会简洁很多，并带来近百倍的性能提升（并行指令）：

z = np.dot(w, x) + b

不用显式 for 循环，实现 Logistic 回归的梯度下降一次迭代（对应之前代码的 for 循环部分。这里公式和 NumPy 的代码混杂，注意分辨）：

单次迭代梯度下降算法流程

$Z=w^TX+b=np.dot(w.T, x) + b$$\\ $$A=\sigma(Z)$$\\ $$dZ=A-Y$$\\ $$dw=\frac{1}{m}XdZ^T$$\\ $$db=\frac{1}{m}np.sum(dZ)$$\\ $$w:=w-\sigma dw$$ $$b:=b-\sigma db$

8）Broadcasting in Python

Numpy 的 Universal functions 中要求输入的数组 shape 是一致的。当数组的 shape 不相等的时候，则会使用广播机制，调整数组使得 shape 一样，满足规则，则可以运算，否则就出错。

四条规则：

让所有输入数组都向其中 shape 最长的数组看齐；

输出数组的 shape 是输入数组 shape 的各个轴上的最大值；

如果输入数组的某个轴和输出数组的对应轴的长度相同或者其长度为 1 时，这个数组能够用来计算，否则出错；

当输入数组的某个轴的长度为 1 时，沿着此轴运算时都用此轴上的第一组值。

9）A note on python or numpy vectors

虽然在Python有广播的机制，但是在Python程序中，为了保证矩阵运算的正确性，可以使用reshape()函数来对矩阵设定所需要进行计算的维度，这是个好的习惯；

如果用下列语句来定义一个向量，则这条语句生成的a的维度为（5，），既不是行向量也不是列向量，称为秩（rank）为1的数组，如果对a进行转置，则会得到a本身，这在计算中会给我们带来一些问题。

a = np.random.randn(5)

如果需要定义（5，1）或者（1，5）向量，要使用下面标准的语句：

a = np.random.randn(5,1)
b = np.random.randn(1,5)

可以使用assert语句对向量或数组的维度进行判断。assert会对内嵌语句进行判断，即判断a的维度是不是（5，1），如果不是，则程序在此处停止。使用assert语句也是一种很好的习惯，能够帮助我们及时检查、发现语句是否正确。

assert(a.shape == (5,1))

可以使用reshape函数对数组设定所需的维度

a.reshape((5,1))

10）Explanation of logistic regression cost function（选修）

在前面的逻辑回归中，我们可以把预测值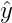 $\hat{y}$ 可以看作预测输出为正类（+1）的概率：

$\hat{y}=P(y=1|x)$

当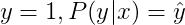 $y=1,P(y|x)=\hat{y}$ ； $y=0,P(y|x)=1-\hat{y}$

将两种情况整合到一个式子中，可得：

$P(y|x)=\hat{y}^y(1-\hat{y})^{(1-y)}$

对上式进行log处理（这里是因为log函数是单调函数，不会改变原函数的单调性)；

$logP(y|x)=ylog(\hat{y})+(1-y)log(1-\hat{y})$

概率P(y|x)越大越好，即判断正确的概率越大越好。这里对上式加上负号，则转化成了单个样本的Loss function，我们期望其值越小越好：

$L(\hat{y},y)=-(ylog(\hat{y})+(1-y)log(1-\hat{y}))$

对于m个训练样本来说，假设样本之间是独立同分布的，我们总是希望训练样本判断正确的概率越大越好，则有：

$max\prod_{i=1}^{m}P(y^{(i)}|x^{(i)})$

同样引入log函数，加负号，则可以得到Cost function：

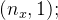
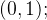
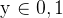
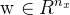
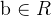
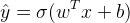
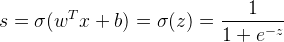
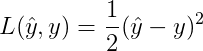
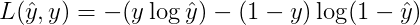
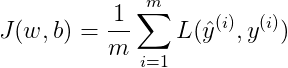
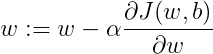
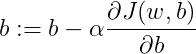
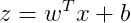
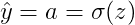
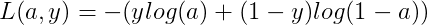
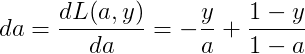
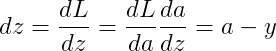
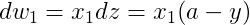
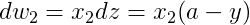
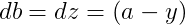
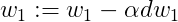
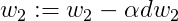
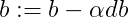
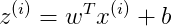
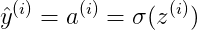
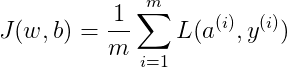
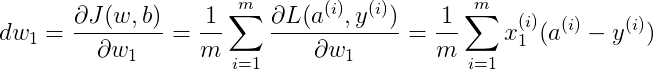
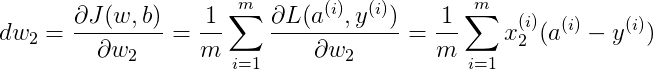
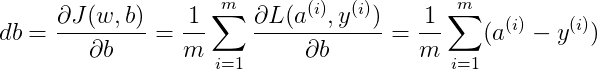
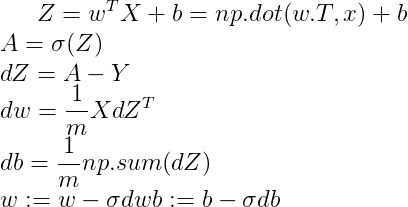
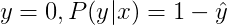
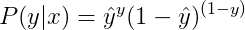
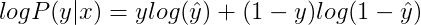
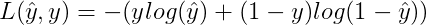
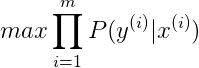
$$$J(w,b) = \frac{1}{m}\sum_{i=1}^mL(\hat{y}^{(i)},y^{(i)})=-\sum_{i=1}^{m}(y^{(i)}log\hat{y}^{(i)}+(1-y^{(i)})log(1-\hat{y}^{(i)})]$

下面，我们要开始本周的编程作业了。