先看例子会好理解一点
什么是图?
本文针对的图主要是有向图,具体定义先不给出,先看一个具体例子:
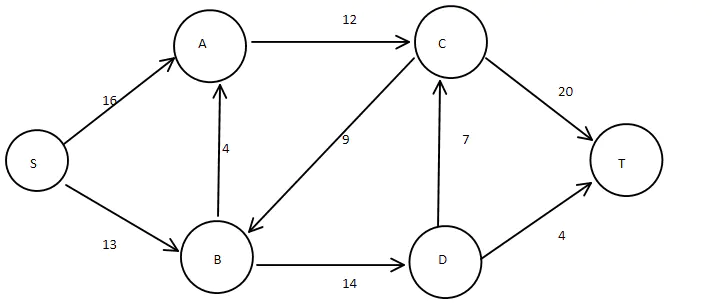
图1:示例有向图
上图就是一个有向图,不用看官方定义,我们自己就能给出自己的定义:
1. 有向图包含了顶点与边;
2. 每一条边有两个端点,并且指明了两个端点之间的指向方向;
3. 每一条边有对应的值(具体含义与具体的模型化场景有关)。
以上定义虽然不是官方定义,但在本文中,这样的定义已经足够使用。为了更好的描述我们总结的定义,所以我给出一个形式化的有向图定义:
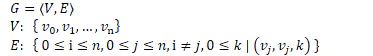
图2:有向图形式化定义
上述定义中,V表示为顶点集合,E表示为有向边集合。当k=0,那么就表示两个顶点之间的有向边无效。
什么是最大流?
在正式开始介绍最大流之前,必须将前一章节中一个遗留的小问题确定下来,那就是有向边的数值到底是什么含义?这里将其定义为边的容量,代表了该边所能通过的最大值。在网络上有很多类比,比如有些类比把有向图看作是水管,容量就是能够通过该水管段最高单位流量。基于此类比,最大流就是从起点到终点所能达到的最高单位流量。为了下文表示上的方便,将容量、最大流都给出一个形式化的定义:
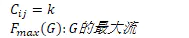
图3:容量以及最大流定义
(以上两个公式太丑陋,第一个容量定义公式,可能让读者产生是一个固定值得歧义理解,实际想要表达的含义是容量就是有向边绑定的数值。最大流定义也同样丑陋,实在不知道该如何表示更加好,所以直接使用了中文描述,对于以上丑陋的表达,我深表歉意。)
最大流的计算方法
为了有效地描述算法,所以必须在具体描述之前再引入几个定义,(很抱歉,会有这么多定义产生,但还是恳请读者耐心一下):
通路:从图起点(S)到达图结束点(T)的路径,由一系列顶点组成;
通路流量:该通路上所能达到的最大单位流量;
饱和边:容量等于通路流量的有向边。
具体算法描述:
Step1:初始化最大流Flow=0;
Step2:在图中找一条通路,如果通路不存在,则结束;
Step3:Flow = Flow+通路流量;
Step4:对通路上所有边的容量进行更新 Cij = Cij-通路流量;
Step5:跳转Step2
注意:在上述算法中,当容量为0时,代表该边已经无效,不能作为通路路经中的边。
算法的有效性解读:
这里使用了解读,而没有使用证明,也就表示以下说法是从一种直观的角度来描述,不是严谨的推理证明。算法是有效的,因为当图中已经没有通路的时候,已经不可能再增加图的流量,所以至少已经达到了本次计算过程中的最大流。剩下的另一部份就是如何来说明通路选择的顺序与最终计算的最大流结果无关?如果两条通路之间是独立的,那么先选择的通路不会对后选择的通路产生影响。如果两条通路并非独立,那么也是可以简单证明通路的先后选择与这两条通路上的最大流无关。如果两条通路的可以被证明,那么将两条通路看作一条通路,证明N+1情况下同样成立。
什么是最小割?
一个割就是一组边的集合,将给集合边从图中边集合中移除,那么图被分割为两个部分,这两个部分之间没有任何边连接。如果说得有点绕口,那么最简单来说,一块肉被从中间隔开,分成两个部分,中间断开的连接的集合就是割。
最小割就是将图切割为两个部分时,代价最小的割的集合,代价就是边上容量的和(S部分到T部分边的容量)。还是拿猪肉作类比,最小割就是找到一块肉连接最小的部分,一刀劈开,那个部分的连接就是最小割。
如何找到这个最小割?
当一个图被割分成两个部分时,不再存在S到T的通路,所以割的代价必定大于等于图的最大流(这个需要添加额外说明吗?应该不需要吧,算是非常明显的结论了吧)。那么也就是说,割的代码最小不能小于图的最大流,也就是割的代价等于图的最大流。
现在确定了割的代价,但如何去找到这样一组割?在进行具体算法说明之前,给出额外一个概念:
影响边:在计算最大流的算法中,会对边的容量进行修改,而将一条通路中修改后容量为0的边称为修改后容量非0边的影响边;
算法描述:
Step1: 初始化边影响边集合;
Step2: 初始化最小割边集合;
Step3: 记录边的原始容量Rij=Cij;
Step3: 寻找一个通路,如果没有通路,则结束;
Step4: 修正边的容量Cij = Cij-通路流量;
Step5: 在通路的边中找一个Cij=0的边,作为预切割边;
Step6: 如果预切割边的容量等于该边的原始容量(Cij=Rij),那么将该边加入最小割边集合;否则,找到该边的所有影响边,将影响边从最小割边集合中移出,将该边加入最小割边集合;
Step7: 对通路其他边记录影响边;
算法的有效性解读:
算法的核心原理就是在寻找最大流的过程中,找出一组边代价等于最大流,并且能够将遍历的通路有效分割的边。
实例
按本文描述算法对最初的图进行最小割求解。
步骤1:寻找第一个通路
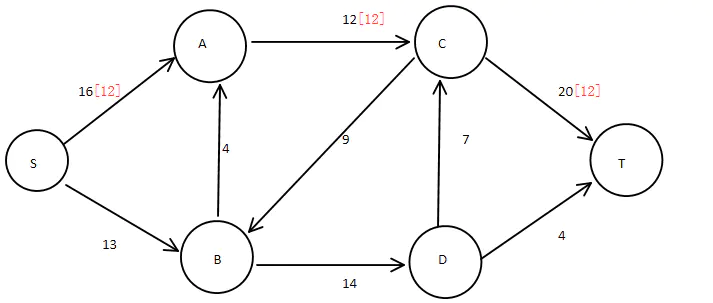
图4:第一条通路标记
红色字体表示该通路的通路流量。根据算法进行容量修正:
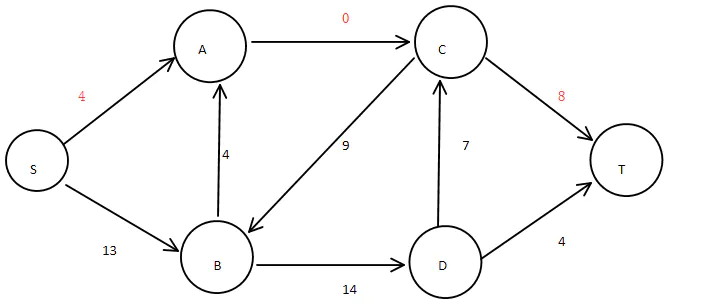
图5:第一条通路容量修正
修改后的容量是用红色字体表示。在此通路中,AC边容量为0,所以将该边加入最小割边集合{AC},同时记录影响边信息,SA的影响边{AC},CT的影响边{AC}。
步骤2:寻找第二条通路:
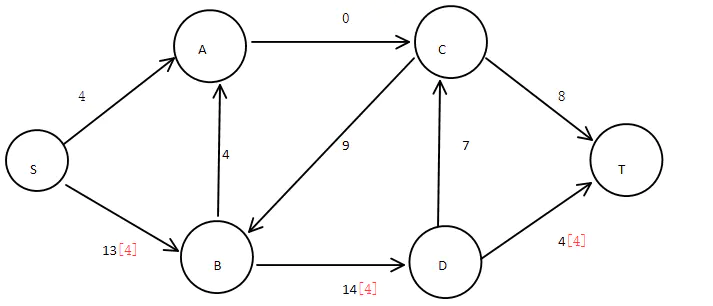
图6:第二条通路标记
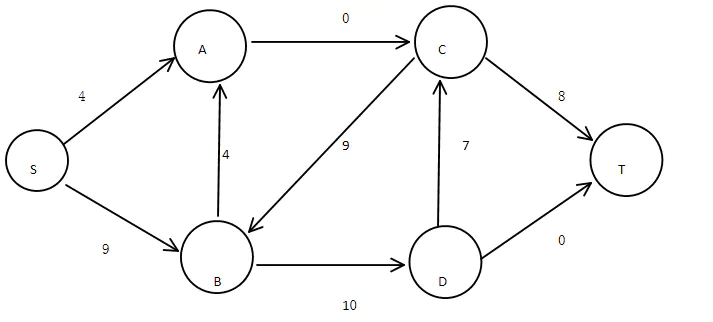
图7:第二条通路容量修正
此时,最小割边集合为{AC,DT}
步骤3:寻找第三条通路:
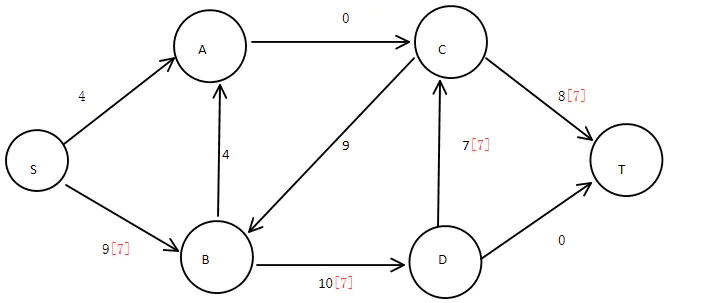
图8:第三条通路标记
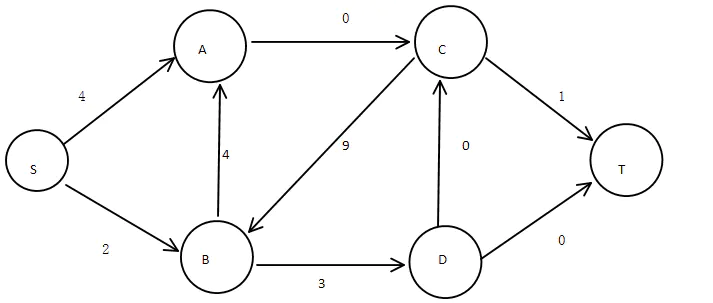
图9:第三条通路容量修正
此时最小割边集合为:{AC,DT,DC}
此时,已经不再存在通路,所以当前最小割边集合就是求解的最小割,其代价为23。
结束语
本文中关于最小割的算法描述没有参考具体算法,只是在看最大流算法时自然而然就产生的一个算法,所以此算法没有被其他文献描述,本人不禁止读者将该算法使用在自己的项目以及论文等文档编写中,但务必在使用前告知作者。
作者:波波2
链接:https://www.jianshu.com/p/beca253fdc9f
来源:简书
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。