洛谷P3455(莫比乌斯反演+整除分块)

题目：click
题意：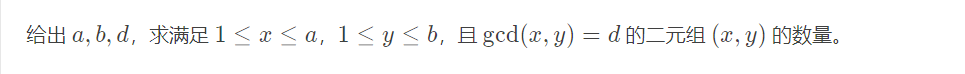
基本与HDU1659思路相同。
唯一点，数据量不同，O(n)的复杂度仍然会T。这里用到了整除分块。
能够在O( $\sqrt{n}$)的复杂度内解决。

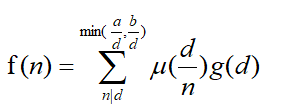
即求f(1）的值，我们需要更快求出 $\sum_{1}^{min(a/d,b/d)}\mu(d)g(d)$。
可以自己写写数据比方说8:
$8/1=8$
$8/2=4$
$8/3=8/4=2$
$8/5=8/6=8/7=8/8=1$
分块为[1,1],[2,2],[3,4],[5,8]，每个区间值相同。
证明可以在网上找一下。
$\sum_{1}^{min(a/d,b/d)}\lfloor{\frac{n}{d}}\rfloor$就可以以O( $\sqrt{n}$)的复杂度求出，而一个区间值一样，只需对莫比乌斯函数做一个前缀处理。

分块代码：

    for(int l=1,r;l<=n;l=r+1)
    {
        r=n/(n/l);
        ans+=(r-l+1)*(n/l);//求和
    }

#include<cmath>
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cstdlib>
#include<istream>
#include<vector>
#include<stack>
#include<set>
#include<map>
#include<algorithm>
#include<queue>
#define inf 0x3f3f3f3f
#define llinf 0x3f3f3f3f3f3f3f3f
#define MAX_len 500005*4
using namespace std;
typedef long long ll;
typedef pair<int,int> PP;
long double eps=1e-9;
const int MAXlen=5e4+10;
int prime[MAXlen];
int tot=0;
int mu[MAXlen];
bool vis[MAXlen];
void init()
{
    tot=0;
    memset(mu,0,sizeof(mu));
    memset(vis,false,sizeof(vis));
    vis[0]=vis[1]=true;
    mu[1]=1;
    for(int i=2;i<MAXlen;i++)
    {
        if(!vis[i])
        {
            prime[tot++]=i;
            mu[i]=-1;
        }
        for(int j=0;j<tot&&i*prime[j]<MAXlen;j++)
        {
            vis[i*prime[j]]=true;
            if(i%prime[j]==0)
            {
                mu[i*prime[j]]=0;
                break;
            }
            else
            {
                mu[i*prime[j]]=-mu[i];
            }
        }
    }
}
ll sum[MAXlen];
int main()
{
    memset(sum,0,sizeof(sum));
    init();
    for(int i=1;i<=MAXlen;i++)
        sum[i]=sum[i-1]+mu[i];
    int T;
    scanf("%d",&T);
    while(T--)
    {
        ll a,b,d;
        scanf("%lld %lld %lld",&a,&b,&d);
        ll temp=min(a/d,b/d);
        ll l,r;
        ll ans=0;
        a/=d;
        b/=d;
        for(l=1;l<=temp;l=r+1)
        {
            r=min(a/(a/l),b/(b/l));
            ans+=(a/l)*(b/l)*(sum[r]-sum[l-1]);
        }
        printf("%lld\n",ans);
    }
    return 0;
}