数据结构（十六）——左高树（含合并过程详细图解）

文章目录

前言
左高树

什么是左高树?
为什么要使用左高树?

最大左高树实现及复杂度分析

节点类和最大左高树类
合并方法
插入(push)、删除(pop）
初始化

左高树合并图解

前言

看到左高树的时候，对左高树的印象大概只有左高树这三个字了。看的时候费劲了一点，因为不知道这个数据结构是干嘛的。网上的资料也比较少。所以这篇文章理解能力有限，请见谅。

左高树

什么是左高树?

左高树大致分为高度优先左高树和重量优先左高树两类。
本文以高度优先左高树为例。

左高树中定义了几个新的概念，比如外部节点、内部节点和扩充二叉树。

外部节点：一类特殊的节点，假设原本的树中节点x的任意孩子节点为空，可以将该指针指向外部节点。
内部节点：至少有一个孩子节点不为空的节点叫做内部节点。
扩充二叉树：增加了外部节点的二叉树。

我原以为这是很重要的概念，但是后面函数实现中却不曾用过。所以我暂且认为这几个概念是为了更形象的定义s(x)。

s(x)是一个函数，代表了内部节点x到其子树外部节点的最短路径。

如果x是外部节点，那么s(x）= 0。

如果x是内部节点 ,那么s(x) >= 1.

如果x的一个孩子s(x1) = 1,另一个孩子s(x2) = 2,那么s(x) = 2

一颗二叉树称为高度优先二叉树（height-biased leftist tree,HBLT）。当且仅当其任何一个内部节点的左孩子的s(x) 值都大于或等于右孩子的s值。

++++++++++++++++++++分割线+++++++++++++++++++++++++++++++++++++++++++

在之后的二叉树实现中，所有结点都为内部节点，即叶节点也为内部节点，且叶节点的s(x) = 1。也就是说外部节点隐式存在。

为什么要使用左高树?

书上的解释为堆(Heap)并不适合所有优先级队列的应用，尤其是当两个优先级队列或多个长度不同的队列需要合并时，需要使用左高树，左高树可在对数时间内实现两个优先级队列的合并。

假设有两个优先级队列，节点数为n、m。且n>m。
不考虑节点数的增长，用堆实现合并时间复杂度至少需要O(mlogn)，即一个节点一个节点插进去。
而左高树的可以在 O(log(mn)) 的时间复杂度下实现合并。

优势已经显现

撒，我们马上实现试试！

最大左高树实现及复杂度分析

最大左高树：是左高树也是大根树。
因为左高树需要表示优先级队列，需要维护节点的优先级，所以是一颗左高树的同时也需要是一颗大根/小根树。

节点类和最大左高树类

template <class T>
class HBLTNode
{
friend MaxHBLT<T>;
public:
    HBLTNode(const T& e, const int s)
    {
        data = e;
        this->s = s;
        leftChild = rightChild = NULL;
    }

private:
    int s;
    T data;
    HBLTNode<T>* leftChild;
    HBLTNode<T>* rightChild;

};

// 最大HBLT类

template <class T>
class MaxHBLT
{
public:
    MaxHBLT(){root = NULL;}
    ~MaxHBLT(){free(root);}
    const T& top(){if(!root) throw "Tree is empty.";}

    void push(const T& x);
    const T& pop();
    MaxHBLT<T>& meld(HBLTNode<T>& x)
    {
        meld(root, x.root);
        x.root = NULL;
        return *this;
    }

    void initialize(T a[], int n);

private:
    void free(HBLTNode* t);
    void meld(HBLTNode* x, HBLTNode* y);
    HBLTNode* root;
};

合并方法

template <class T>
void mexHBLT<T> :: meld(HBLTNode* x, HBLTNode* y)
{
    // 合并后左高树以x为根，返回x的指针
    if(y == NULL)
        return;
    if(x == NULL)
    {
        x = y;
        return;
    }
    // x和y都不空，必要时交换x和y,直接交换节点地址，真ne到
    if(x->data < y->data)
        swap(x, y);

    // 目前x->data >= y->data

    // 继续在右路径合并
    meld(x->rightChild, y);

    // 因为swap函数不处理空对象，单独交换
    if(x->leftChild == NULL)
    {
        x->leftChild = x->rightChild;
        x->rightChild = NULL;
        x->s = 1;
    }
    else // 如果右边的s(x)比左边大，不符合左高树规则，交换
    {
        if(x->leftChild->s < x->rightChild->s)
            swap(x->leftChild, x->rightChild);
        x->s = x->rightChild->s + 1;
    }
}

时间复杂度：

遍历沿右路径进行，所以递归次数应该为两个树根节点的s(x)加起来，设两个树的节点数目为m、n。那么两颗树的s(x)最大为log(m+1)、log(n+1)（因为s(x)小于等于完全二叉树的高度）。
那么时间复杂度为O(logm+logn) = O(log(mn))

插入(push)、删除(pop）

template <class T>
void MaxHBLT<T> :: push(const T& x)
{
    HBLTNode<T> *q = new HBLTNode<T>(x, 1);
    meld(root,q);
}

template class<T>
const T& MaxHBLT<T> :: pop()
{
    T res;
    if(root == NULL)
        throw "The tree is empty.";

    res = root->data;

    HBLTNode<T>* l = root->leftChild;
    HBLTNode<T>* r = root->rightChild;

    delete root;
    root = l;
    meld(root, R);

    return res;
}

时间复杂度：

插入每次插入一个节点，逻辑为只有一个节点的树与原有的树合并，根据合并的时间复杂度，m = 1,插入时间复杂度为O(logn)。

删除的逻辑为删除根节点，分为两颗左高树，再将两颗树合并，时间复杂度为O(logn)。

初始化

template <class T>
void MaxHBLT<T> :: initialize(T a[], int n)
{
    Queue<HBLTNode<T>> q(n);
    free(root); //删除原来的树

    for(int i = 1; i <= n; i++)
    {
        HBLTNode<T> *t = new HBLTNode(a[i], 1);
        q.push(t);
    }

    for(int i = 1; i <= n-1; i++)
    {
        HBLTNode<T> *a = q.pop();
        HBLTNode<T> *b = q.pop();
        meld(a, b);
        q.push(a);
    }

    if(n > 0)
        root = q.pop();
}

时间复杂度：

初始化的逻辑为，假设有n个元素，提供一队列，每次pop出两颗树（一个节点也视为一颗左高树），合并后，加入队列，合并(n-1)次，队列中剩下的唯一一颗树变为实现完成的最大左高树。

为什么合并n-1次？

当n为偶数时
假设存在一个以2为公比的等比数列，由求和公式有以下等式成立：

第n项 = 前n-1项部分和 + 1

合并次数就是前n-1项部分和，节点个数便是第n项。
比如有8个元素，需要先合并4次，再合并2次，最后合并1次，共合并7次。

当n为奇数时
可视为在偶数的基础上加了一个元素，多一次合并操作，仍然还是需要合并n-1次。

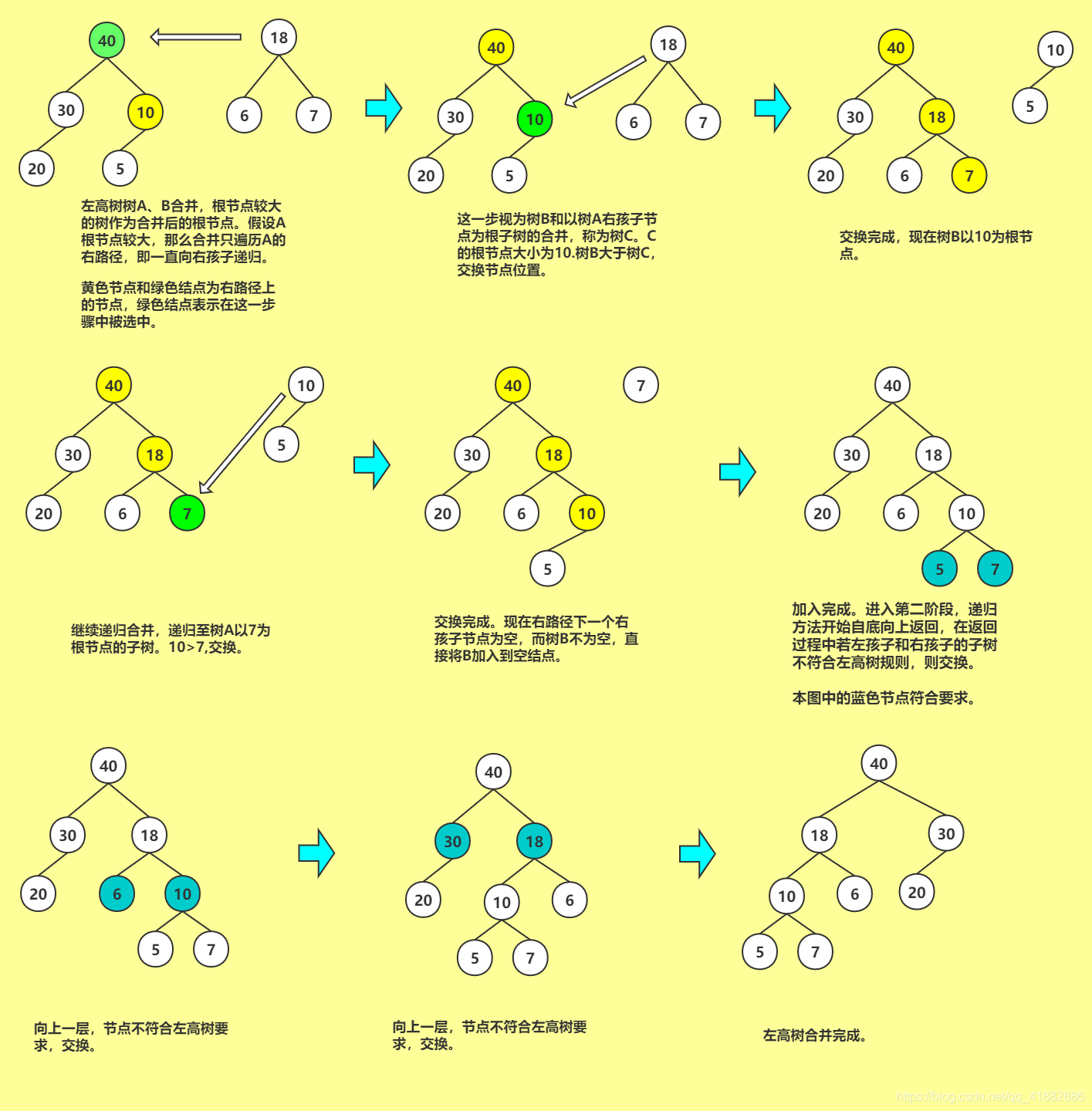
左高树合并图解

因为左高树合并操作我没有找到很细致的图，在理解时捋的合并方法代码，不直观，便自己画了一个，希望可以帮助理解。
在这里插入图片描述