数据结构（二十一）——图和图的应用

前言

本章是数据结构逻辑的最后一种形式，图状结构。因为本章只讲述了图结构的冰山一角，所以结构非常清晰。

图(graph)

图是最复杂的一种数据结构，也是最能表述现实应用的数据结构。人际关系、航线、网络中的节点等等许多接近实际的问题都可以用图来描述。

1）图的基本概念及特性

图：在数据结构领域，我们把图抽象为有限集V和E的有序对，即用边连接在一起的顶点的集合。

就像望月新一证明ABC猜想一样，要学习图，首先要了解图的世界，清楚在图的世界中的术语。

一大堆概念来袭：

1. 顶点(vertex)
2. 有向边(directed edge)与无向边(undirected edge)
3. 有向图(directed graph)与无向图(undirected graph)
4. 邻接(adjacent)与关联(incident)
5. 权(weight)与长度(length)
6. 加权图(weighted graph)与无权图(unweighted graph)
7. 环(loop)
8. 路径(path)与简单路径(simple path)
9. 环路(cycle)
10. 连通(connected)、 强连通(strongly connected)
11. 生成树(spanning tree)
12. 度(degree)、入度(in-degree)与出度(out-degree)
13. 完全图(complete path)与二分图(bipartite graph)

当明白这些概念都在讲什么东西的时候，我们就可以继续往下学习图的某些特性（其实仔细想一下就能推出的特性）：

• 在无向图中，所有节点的度求和 = 边的数量的二倍
• 在有向图中，所有节点的出度求和 = 所有节点的入度求和 = 边的数量

2）图的描述

图的描述其实就是图中的元素如何存储，课本中列举了三种方法，同时这三种方法在在矩阵那一章也出现过。

1. 邻接矩阵(adjacent matrix)：设图中有n个元素，利用 $(n+1)*(n+1)$的二维数组进行存储。
2. 邻接链表(adjacent list)：将图中的节点存储在一个一维数组中，数组中的元素 $i$指向一个链表指针，该链表中存储 $i$的邻接节点。
3. 邻接数组(adjacency array)：将图中的节点存储在一个一维数组中，数组中的元素 $i$指向一个数组指针，该数组中存储 $i$的邻接节点。该二维数组是不规则的。

a. 无权图描述

以下图为例：

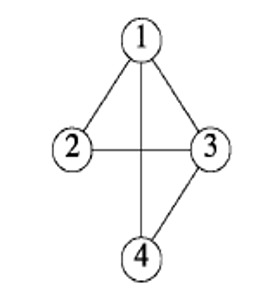
邻接矩阵：

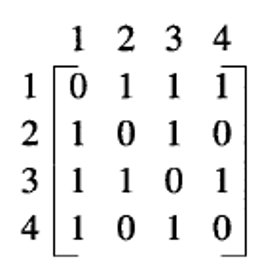
邻接链表：

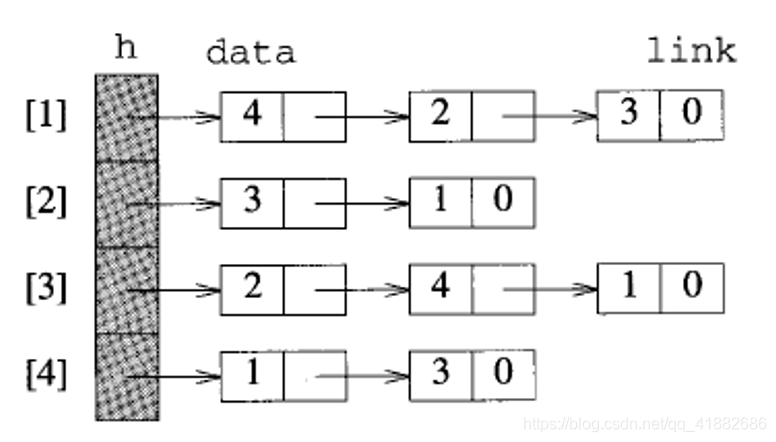
邻接数组：

b. 加权图描述

以下图为例：

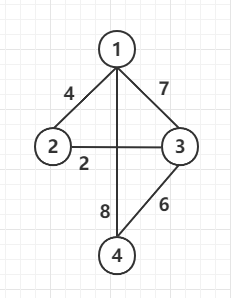
邻接矩阵：

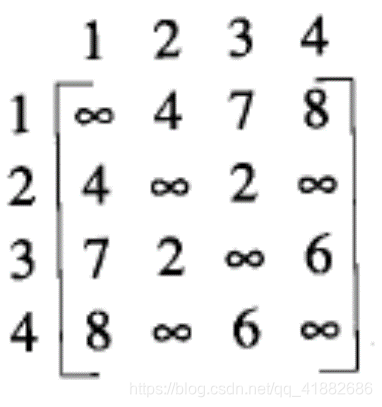
邻接链表：

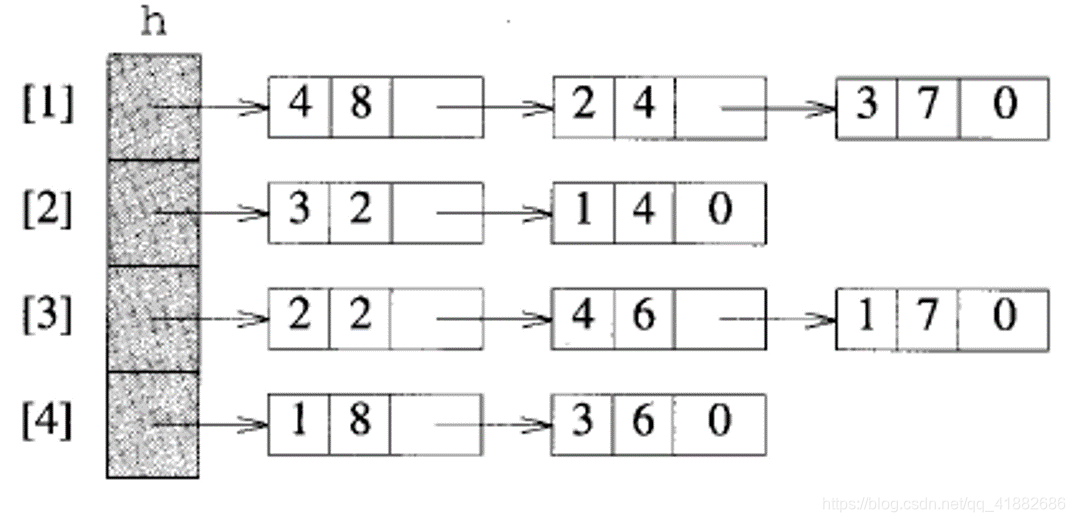
邻接数组：
与无权图的不同是，将数组的对象由T类型改为结构体或pair类型。

3）图的类实现

图的分类：无权无向图、加权无向图、无权有向图、加权有向图
图的描述：邻接矩阵、邻接链表、邻接数组

对于每一种图，都有三种描述与之对应，共有12种类。

类继承图关系如下：

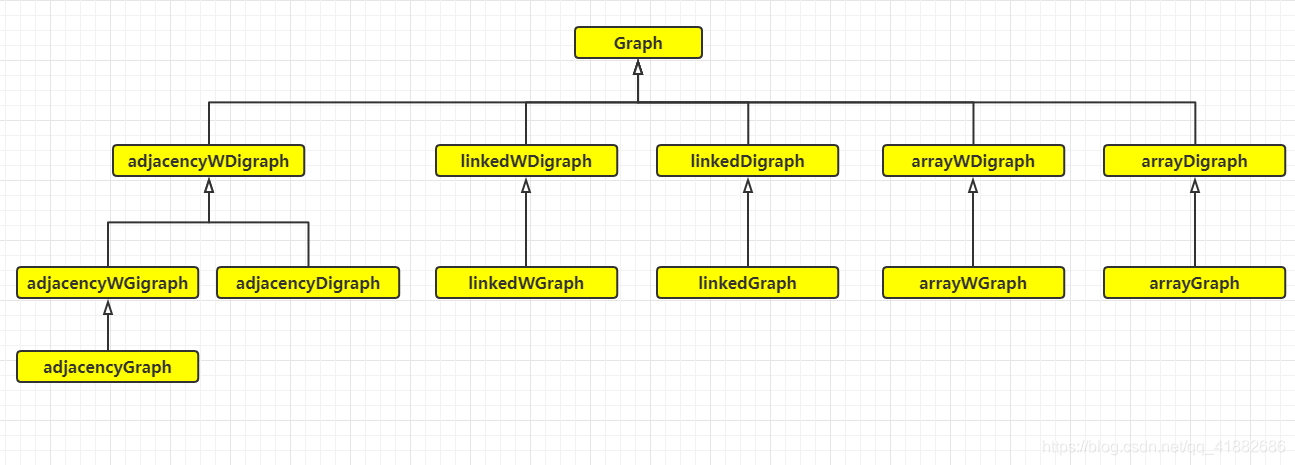
因为图的类实现实在太多，函数也由于描述不同不能实现通用，且函数逻辑都较为简单。我在这里仅写出抽象类 Graph作为参考，以防忘记。

template <class T>

class Graph
{
public:
    virtual ~graph(){}

    //ADT
    virtual int numberOfVertices() const = 0; // 返回节点数量
    virtual int numberOfEdges() const = 0; // 返回边的数量
    virtual bool existsEdge(int, int) const = 0; // 判断一条边是否存在
    virtual void insertEdge(edge<T>*) = 0; // 插入边
    virtual void eraseEdge(int, int) = 0; // 删除边
    virtual int degree(int) const = 0; // 返回某一节点的度
    virtual int inDegree(int) const = 0; // 返回某一节点的入度
    virtual int outDegree(int) const = 0; // 返回某一节点的出度

    virtual bool directed() const = 0; // 当是有向图时，返回true
    virtual bool weighted() const = 0; // 当是加权图时，返回true
    virtual vertexIterator<T>* iterator(int) = 0;// 迭代器,访问指定顶点的相邻节点
};

4）图的遍历

图的遍历即从某一顶点开始，寻找所有可到达的顶点。有两种常用的搜索方法：广度优先搜索(BFS,breadth first search)和深度优先搜索(DFS, deep first search)

a. 广度优先搜索

广度优先搜索利用队列结构，从特定节点开始，遍历所有邻接节点，标记并入队。再依次出队，对于每一个出队的节点，遍历其所有未标记的邻接节点，标记并入队，直到队列为空，算法结束。

因为队列的FIFO属性，搜索过程是宽度优先，即第一次遍历的节点都是和起始节点“距离”为1的节点，第一次遍历入队的节点出队为第二次遍历，第二次都是“距离”为2的节点，第三次…
所以叫做广度优先搜索。

virtual void bfs(int v, int reach[], int label)
{
    Queue<int> q;
    reach[v] = label;
    q.push(v);
    while(!q.empty())
    {
        int p = q.pop();

        //使用迭代器来找到顶点p的所有邻接节点
        vertexIterator<T>* ip = iterator(p);
        int tem;
        while((tem = ip->next()) != 0)
        {
            if(reach[tem] == 0)
            {
                q.push(tem);
                reach[u] = label;
            }
        }
        delete ip;
    }
}

b. 深度优先搜索

深度优先搜索利用栈结构，可以利用递归或者非递归实现。如果使用栈，那么从特定节点开始，遍历其所有邻接节点，标记并加入栈。再依次出栈，对于每个出栈的元素，遍历其未标记的邻接节点，标记并入队，栈为空时，算法结束。

因为栈结构的FILO属性，从初始节点开始，遍历的元素入栈后反向出栈，在每次遍历都有新节点的情况下，每一次出栈的元素与初始点的“距离”都加一。若一次遍历没有发现新节点，下一次出栈的元素较上次出栈的元素“距离”减一。
因为是一股劲冲到最远“距离”，碰壁之后退一格再继续冲，所以叫做深度优先搜索。

// 递归实现
virtual void dfs(int v, int reach[], int label)
{
    Graph<T>::reach = reach; //reach和label为静态数据成员
    Graph<T>::label = label;
    rDfs(v);
}

virtual void rDfs(int v)
{
    reach[v] = label;
    vertexIterator<T> *iv = iterator(v);
    int u;
    while((u=iv->next()) != 0)
    {
        if(reach[u] == 0)
            rDfs(u);
    }

    delete iv;
}

// 非递归实现
virtual void SDfs(int v, int reach[], int label)
{
    Stack<int> s;
    reach[v] = label;
    s.push(v);
    while(!s.empty())
    {
        int p = s.pop();

        vertexIterator<T> *ip = iterator(p);
        int tem;
        while((tem = ip->next()) != 0)
        {
            if(reach[tem] == 0)
            {
                s.push(tem);
                reach[tem] = label;
            }
        }
        delete ip;
    }
}

c. 两种搜索算法的比较

时间复杂度：两种搜索算法的时间复杂度在相同描述下是相同的。在上述的代码中，时间复杂度取决于加入容器的节点数目和迭代器用时。

• 当使用邻接矩阵实现时，时间复杂度为 $O(sn)$, $s$是加入容器的节点数目。
• 当使用邻接链表或邻接数组实现时，时间复杂度为 $\sum_{i}d_{i}^{out}$，其中i是被标记的节点。

空间复杂度：两种搜索算法的空间复杂度都为 $O(n)$。其中有个有趣的现象是两种算法空间性能最好和最坏的情况是相反的。

如下图：

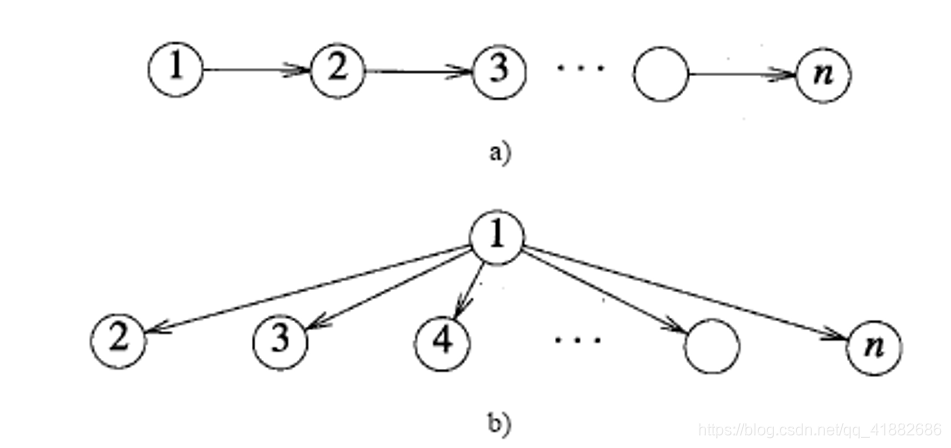
以1为起始点，

• 图a是dfs最坏的情况，因为在到达n之前都不能释放栈空间；同时又是bfs最好的情况，队列中的元素在算法执行时永远不超过1。
• 图b是bfs最坏的情况，因为第一次遍历之后，队列中的元素达到 $n-1$;同时又是dfs最好的情况，栈空间在算法执行时永远不超过1。

5）图的应用

说是图的应用，其实更像是两种搜索算法的应用。

a. 寻找一条路径

寻找一条从源点到目标节点的路径。
可以通过bfs和dfs实现两种不同寻找路径的方法，其中dfs找出的不一定是最短路径，bfs找出的一定是最短路径。

dfs递归实现：

//dfs寻找路径，节点为int类型，返回一个int类型的路径数组
int* findPath_dfs(int source, int goal)
{
    int n = numberOfVertices();
    int* path = new int[n+1];
    path[1] = source;
    int* reach = new int[n+1];

    for(int i = 1; i<=n; i++)
    {
        reach[i] = 0;
    }

    //搜索路径
    if(theSource == goal || rFindPath(source,goal))
    {
        path[0] = length - 1;
    }
    else
    {
        delete[] path;
        path = null;
    }
    delete[] path;
    return path;
}

bool rFindPath(int source, int goal)
{
    reach[source] = 1;
    vertexIterator<T>* is = iterator(source);
    int u;
    while((u = is->next()) != 0)
    {
        if(reach[u] == 0)
        {
            path[++length] = u;
            if(u = goal || rFindPath(u, goal))
                return true;
            length--;
        }
    }
    delete is;
    return false;
}

bfs实现：

//使用bfs寻找最短路径，只需要加一个记录前驱节点的数组

int* findPath_bfs(int source, int goal)
{
    Queue<int> q;
    int* path = new int[n+1];
    int* pre = new int[n+1];
    int* reach = new int[n+1];

    for(int i =0;i<=n;i++)
    {
        reach[i] = 0;
        pre[i] = 0;
    }

    q.push(source);

    while(!q.empty())
    {
        int p = q.pop();

        vertexIterator<T> *ip = iterator(p);
        int u;
        while((u = ip->next()) != 0)
        {
            if(reach[u]==0)
            {
                q.push(u);
                reach[u] = 1;
                pre[u] = p;
                if(u == goal)
                    break;
            }
        }
        if(u == goal)
            break;
    }

    int t = pre[q.pop()];
    int i = 1;
    path[i++] = t;

    t = pre[t];
    while(t != 0)
    {
        path[i++] = t;
        t = pre[t];
    }

    return path;
}

b. 连通及连通构件

搜索方法另一应用是检验无向图是否连通，或者对一个不连通图的连通构件进行标记，判断哪几个节点在同一构件中。

判断是否连通算法的思想十分简单：

//判断是否连通
bool connected()
{
    int n = numberOfVertices();

    int* reach = new int[n+1];

    dfs(1, reach,1);
    for(int i = 1; i <= n; i++)
    {
        if(reach[i] == 0)
            return false;
    }
    return true;
}

判断连通构件个数：

int labelComponents()
{
    int n = numberOfVertices();
    int label = 0;
    int* reach = new int[n+1];


    for(int i = 1; i <= n; i++)
    {
        if(reach[i] == 0)
        {
            label++; // 区分连通构件和记录构件数
            bfs(i, reach, label);
        }
    }
    return label;
}

c. 生成树

进行bfs或dfs时，每遍历一个未到达过的节点，前序节点和该节点形成一个edge。因为不可能遍历已到达的节点，形成的边集不可能有环路，并且由搜索算法可知该边集又是连通的，算法结束后形成一颗树，我们叫做生成树。

由bfs形成的叫做广度优先生成树，由dfs形成的叫做深度优先生成树。

在这里我们只介绍什么是生成树，以后的章节会利用Prim算法和Kruskal算法，寻找最小生成树。