文章目录
- 1. 图的基本概念
- 2. 图的存储
- 3. 基本操作
- 4. 图的遍历
- 5. 图的最小生成树
- 6. 最短路径
- 7. 有向无环图
- 8. 关键路径
- 9. 一些小知识点
1. 图的基本概念
1.1 定义
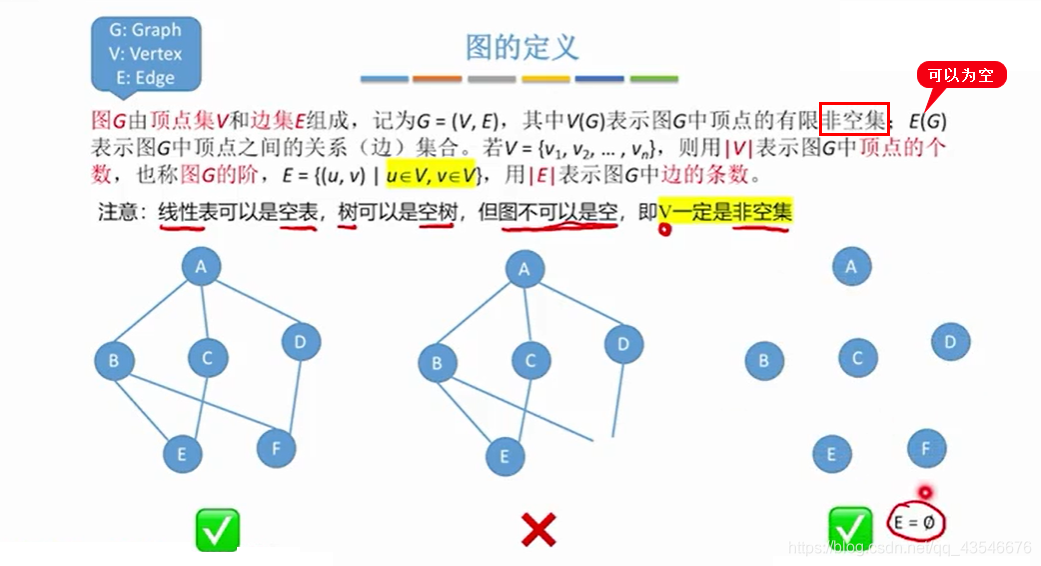
1.2 无向图与有向图
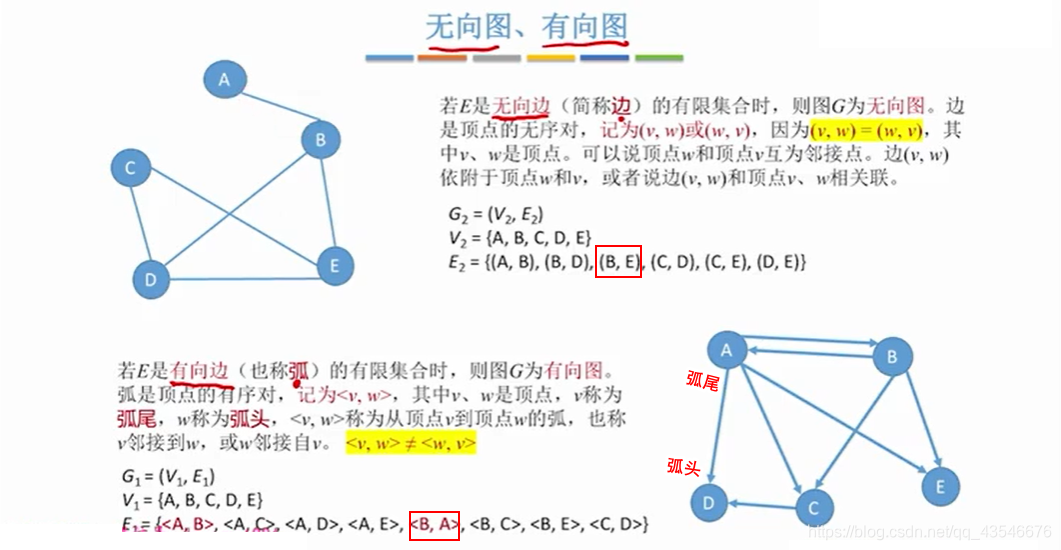
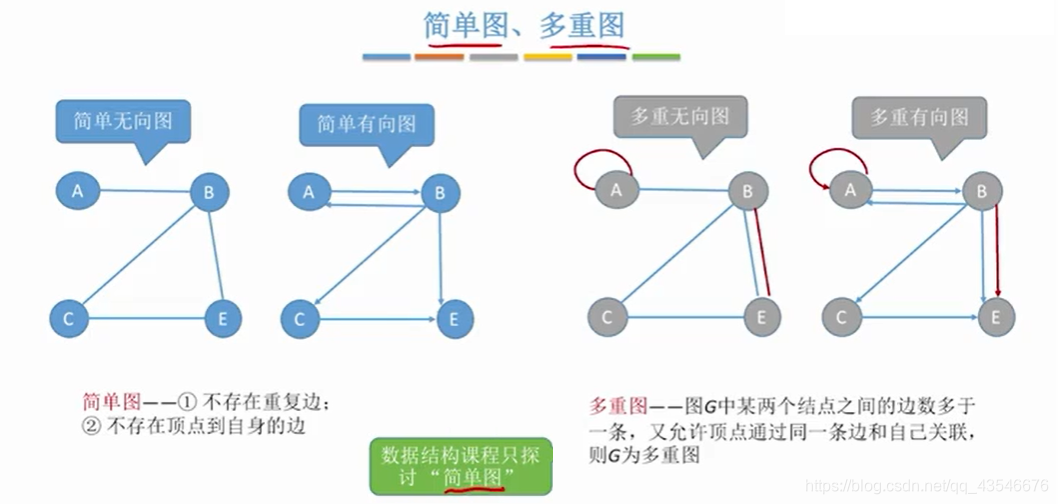
1.3 度
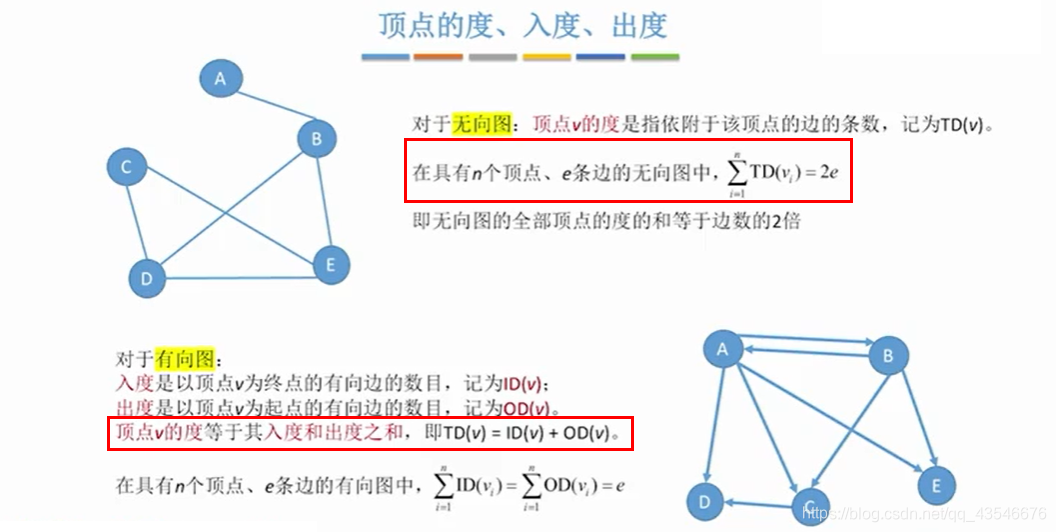
注意:树与图结点的度定义不同。树的度是指每个结点的孩子个数。
1.4 点到点的关系
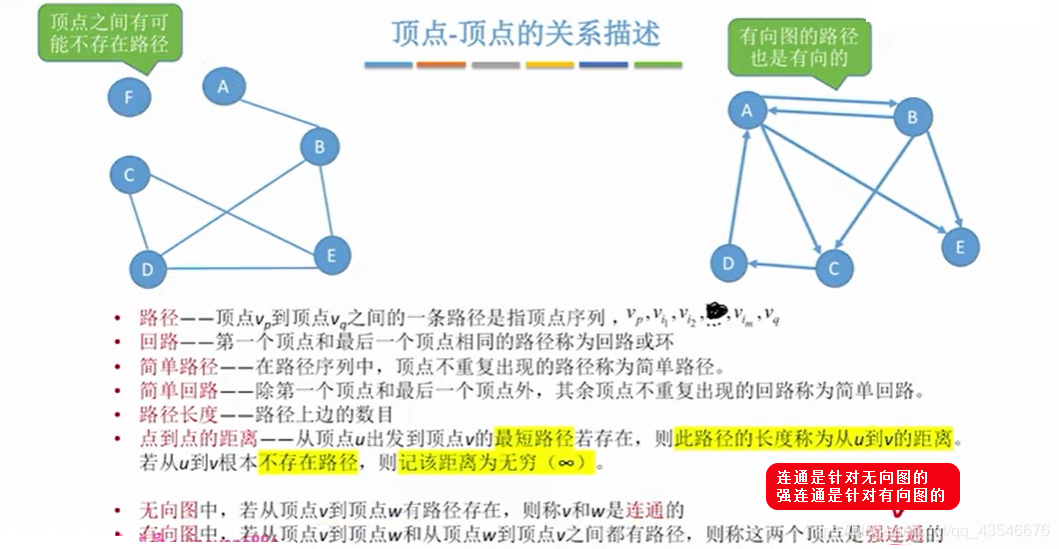
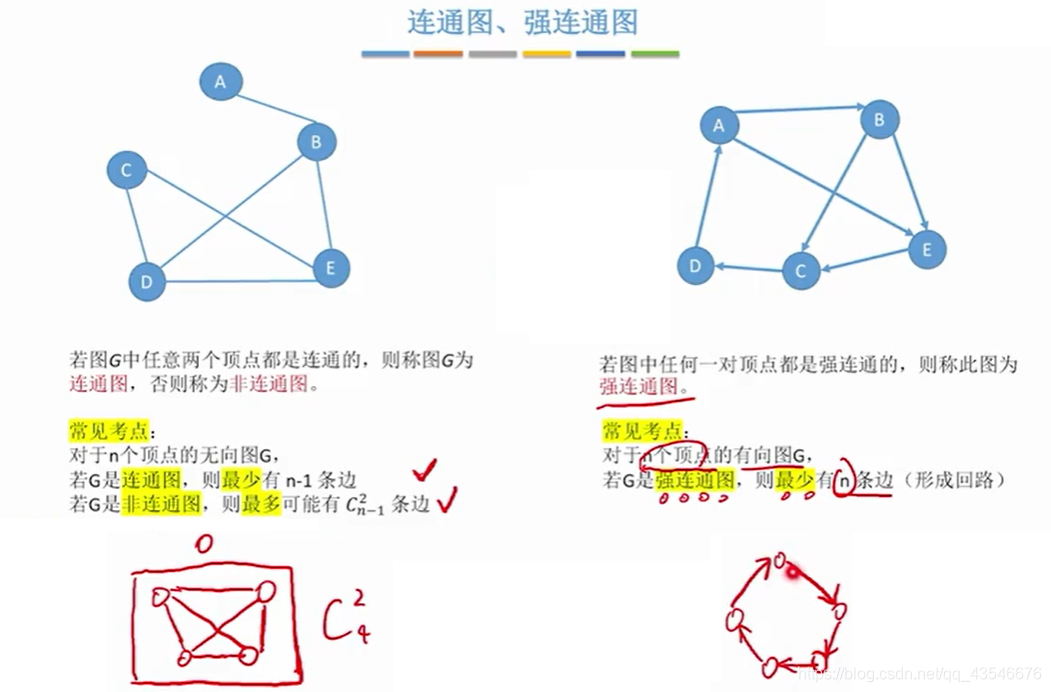
注意:
- 若连通图的边>n-1条,比如有n条边,则该图中一定存在环。
- 如果题目是说,该图在任何情况下都连通,是指这些顶点和多少条边任意组合都是连通图,而不是
n - 1,因为那不满足任意组合。也就是考虑极端情况, 即n-1个顶点构成无向完全图+一条边。即C【2到n-1】 + 1 = (n-1)(n-2)/2 + 1
1.5 图的局部
1.5.1 子图
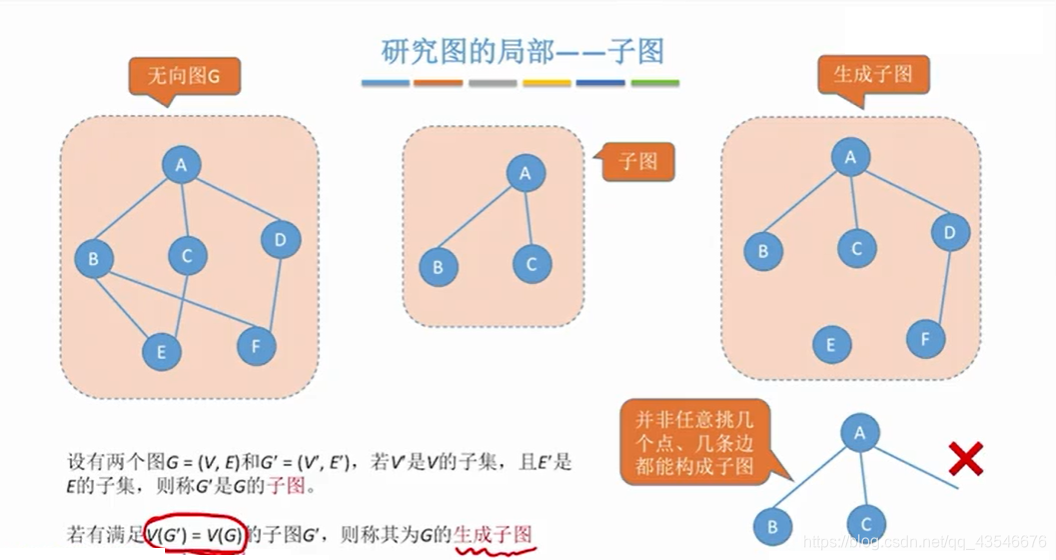
注意:虽然子图是取顶点集的子集和边集的子集,但是如果说取顶点集的子集和边集的子集是子图则错误。
有向图的子图和无向图的子图定义一样。
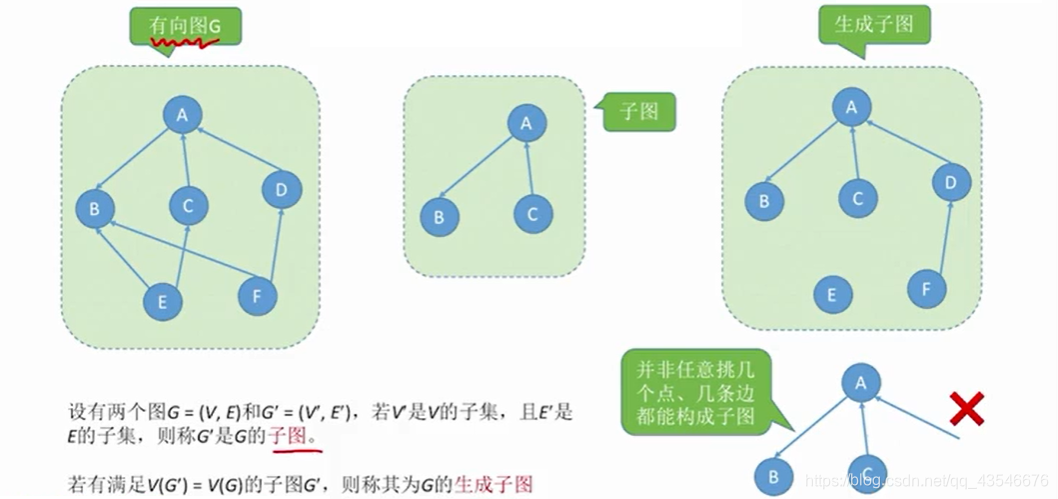
1.5.2 连通分量(极大连通子图)
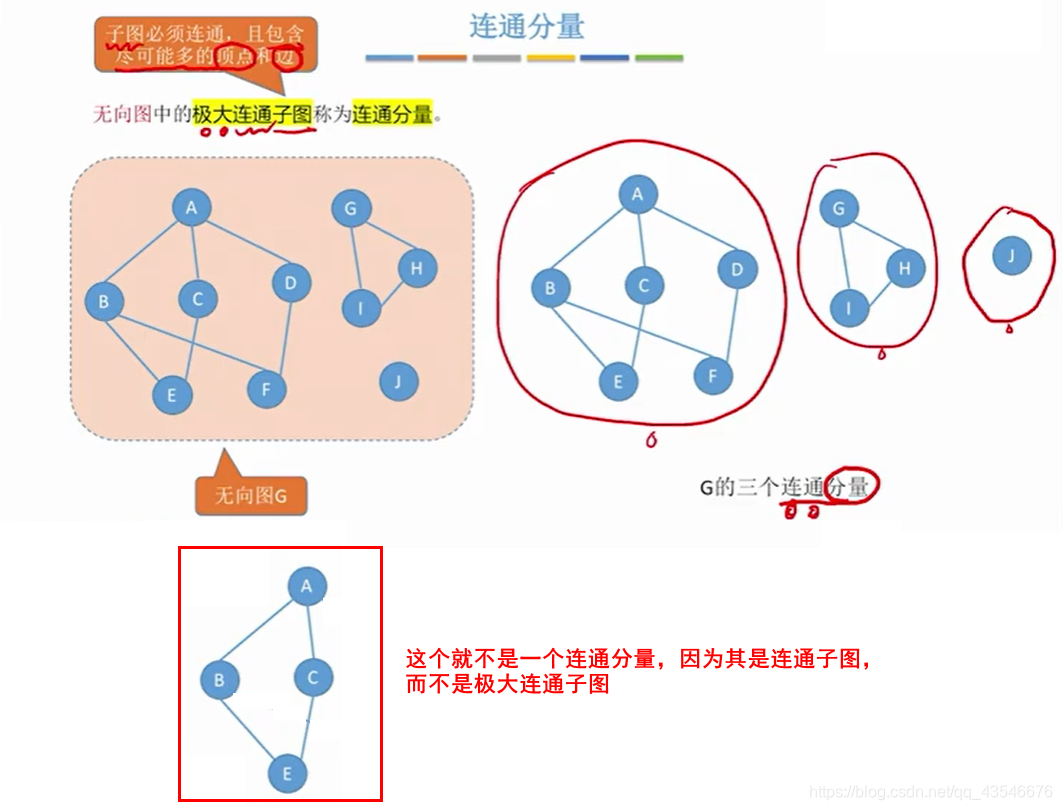
一个图可以有多个连通分量,即多个极大连通子图。
一个图的连通分量数:指该图的极大子图的个数。
1.5.3 强连通分量(极大强连通子图)
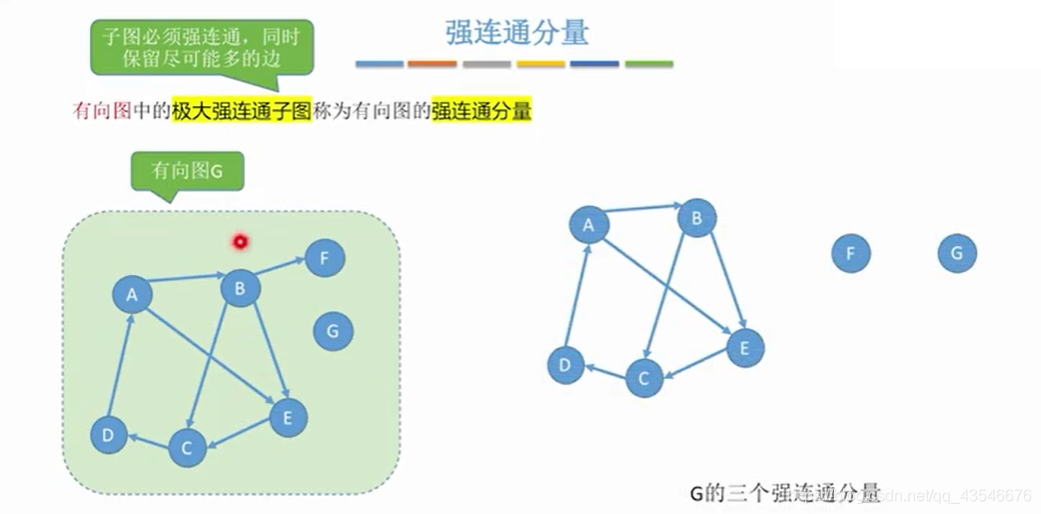
1.5.4 连通无向图的生成树
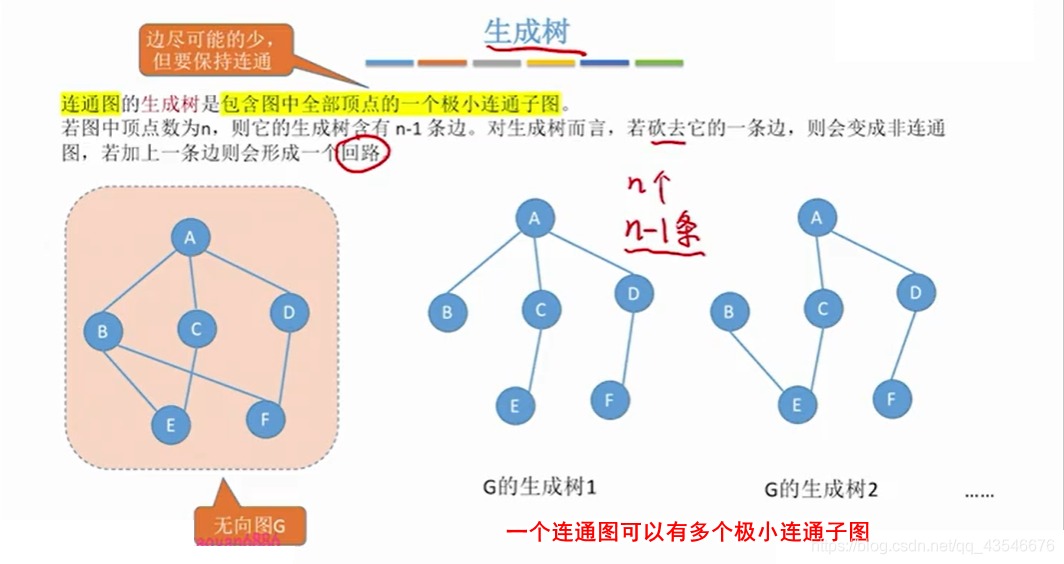
1.5.5 非连通无向图的生成森林
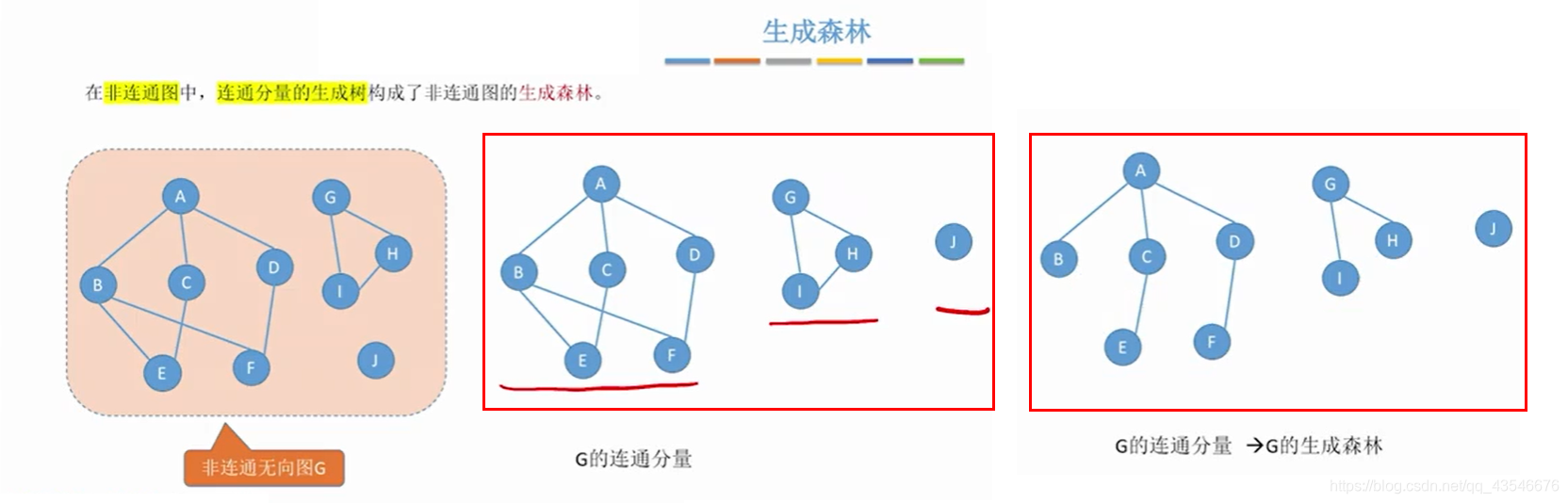
1.5 几种特殊状态的图
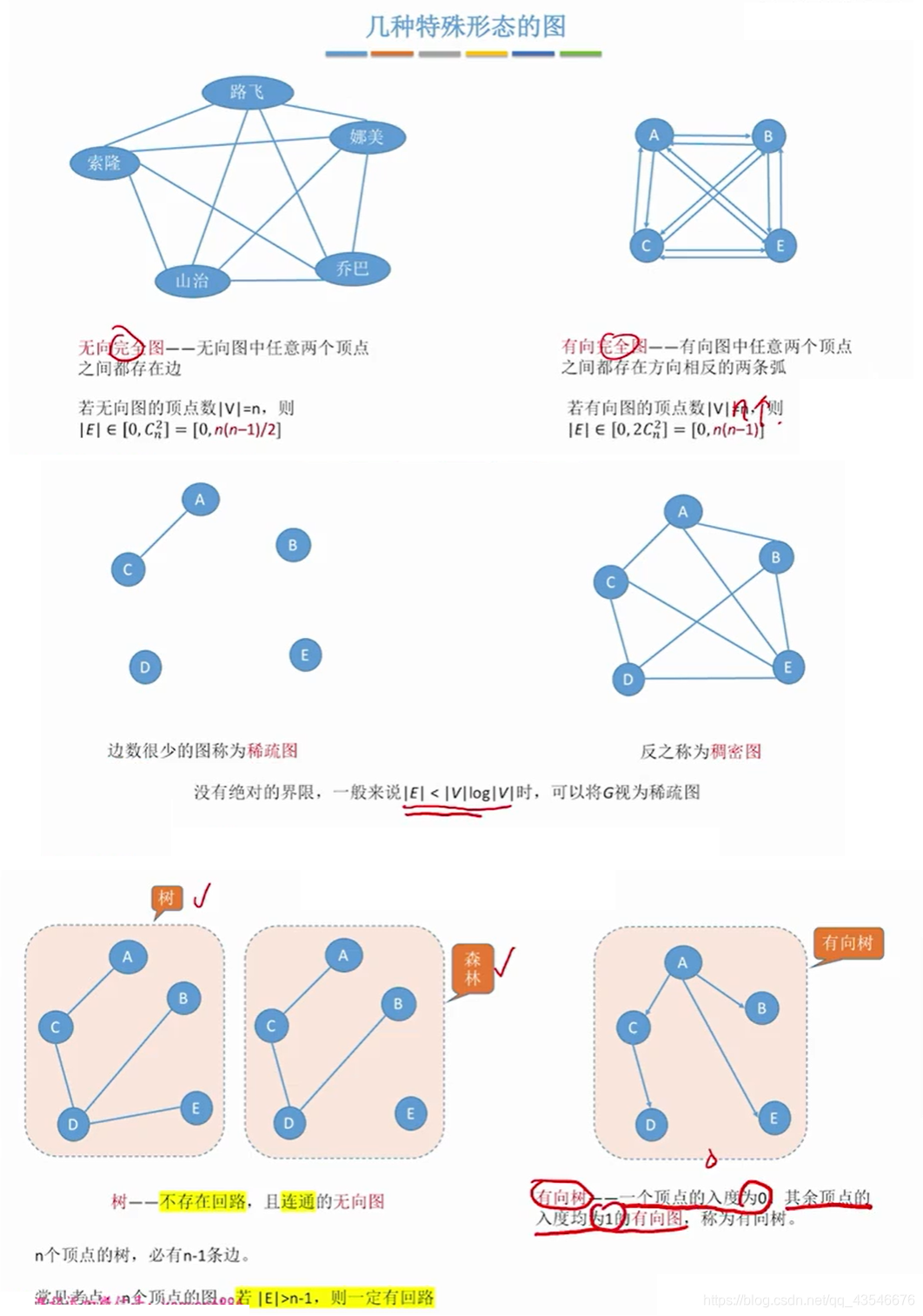
1.6 小结

2. 图的存储
* 图的存储
1. 邻接矩阵(适合稠密的情况)
2. 邻居表法
3. 十字链表
4. 邻接多重表
2.1 邻接矩阵(适合稠密的情况)
2.1.1 存储非带权图
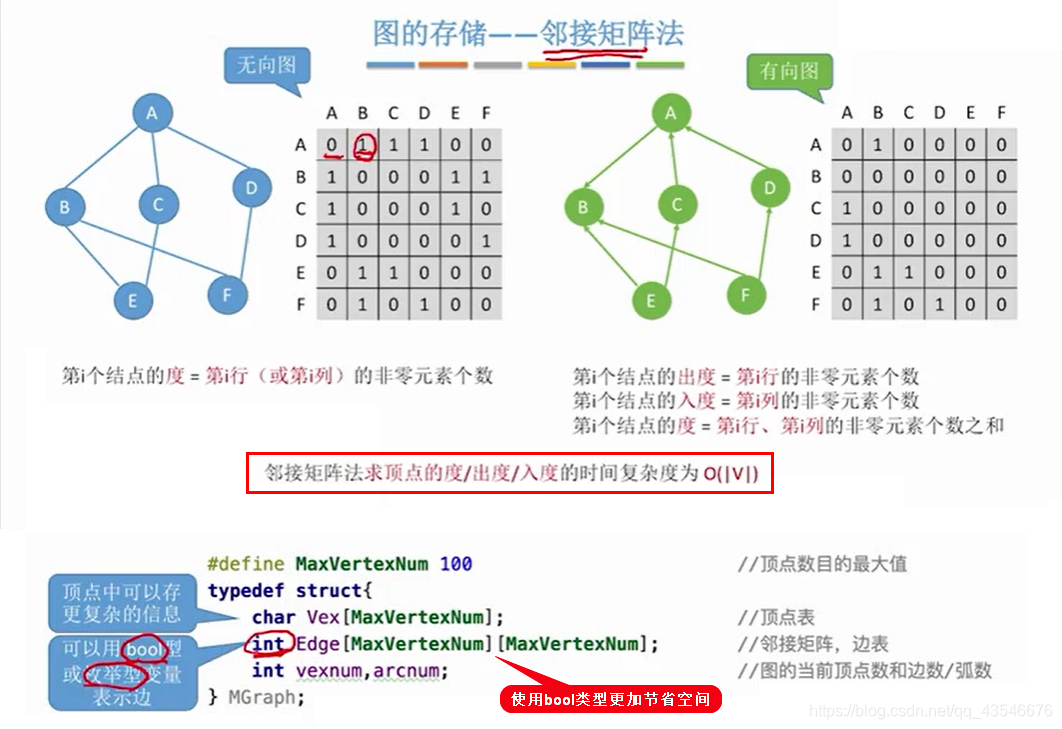
2.1.2 存储带权图
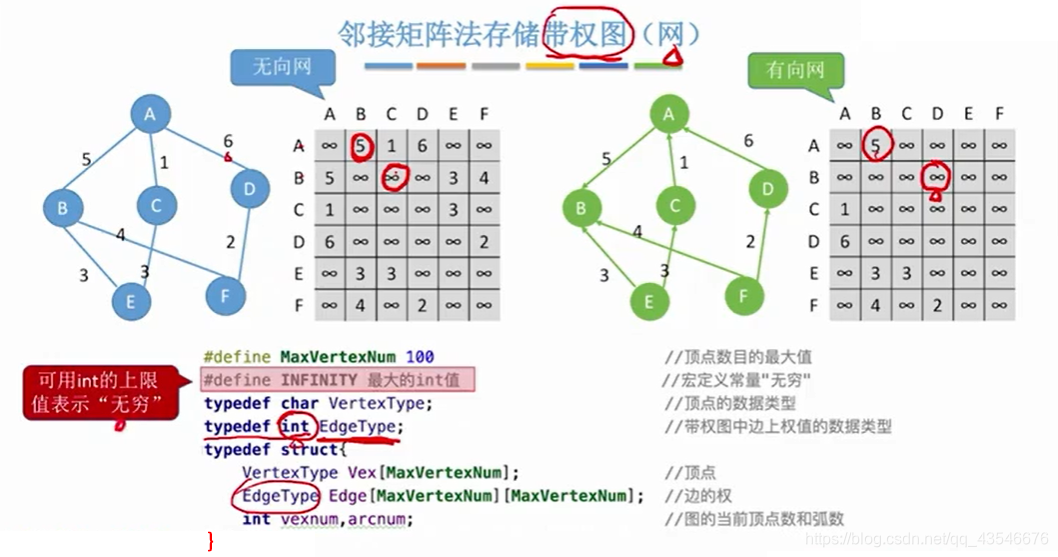
主要是边表变化了,之前存放边关系的二维数组变成了存放边的权重。
2.1.3 邻接矩阵性能分析
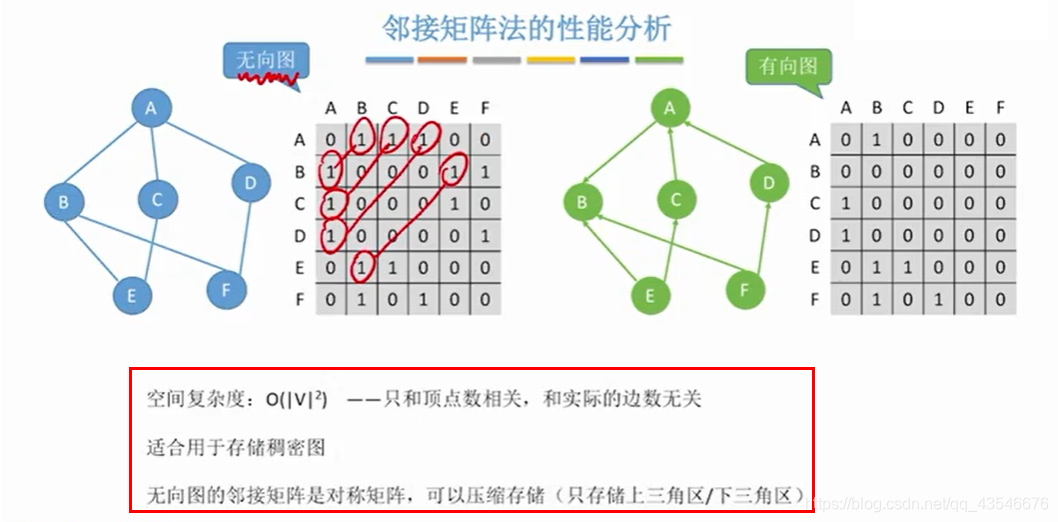
2.1.4 对称邻接矩阵的压缩存储
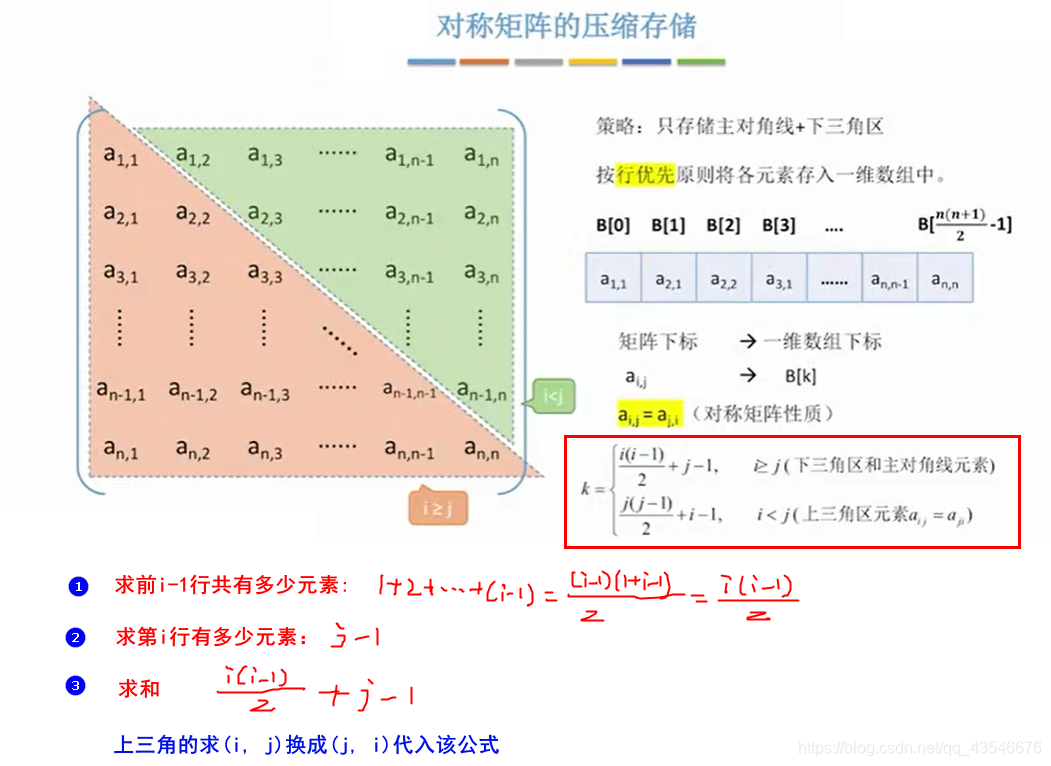
注意:将无向图的对称矩阵,按照出度的大小由高到低或者由低到高排序后再构造矩阵,会构成上三角或下三角的矩阵。
2.1.5 邻接矩阵的一个重要性质
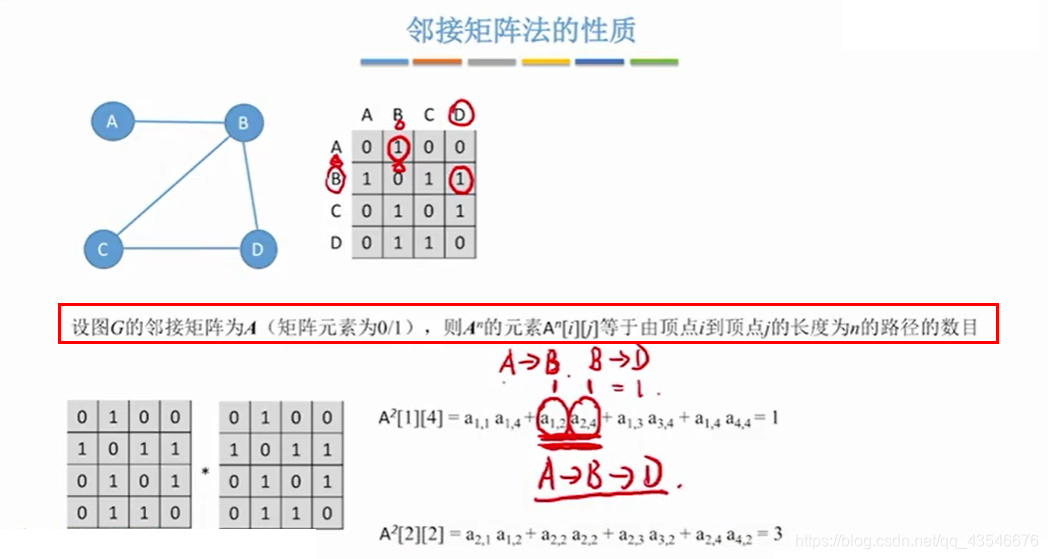
2.2 邻接表法(适合稀疏的情况)
2.2.1 邻接表法
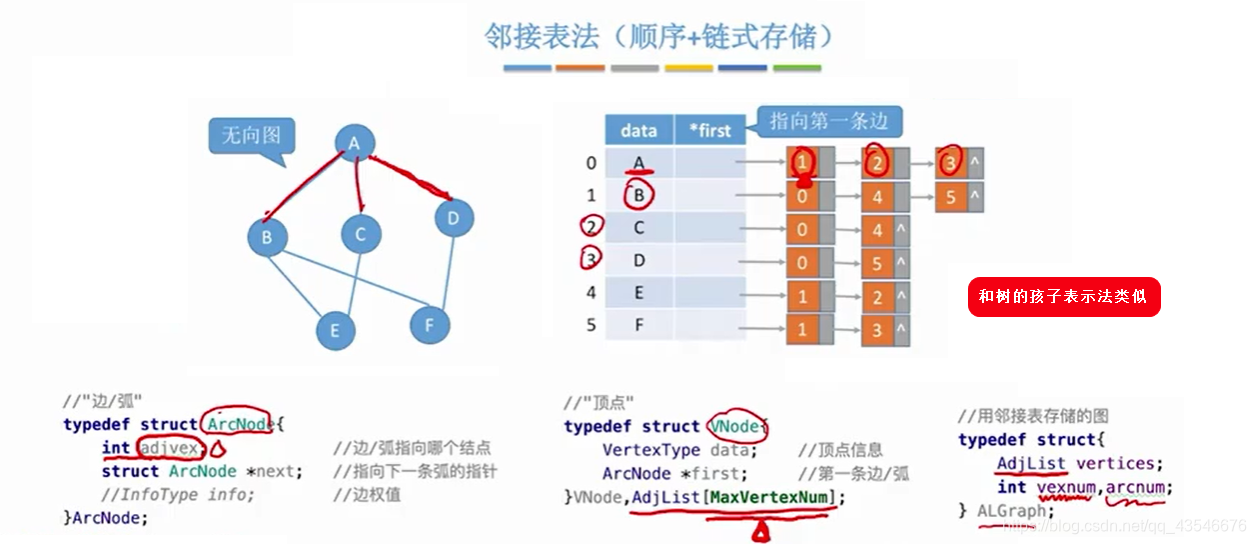
2.2.2 性能分析
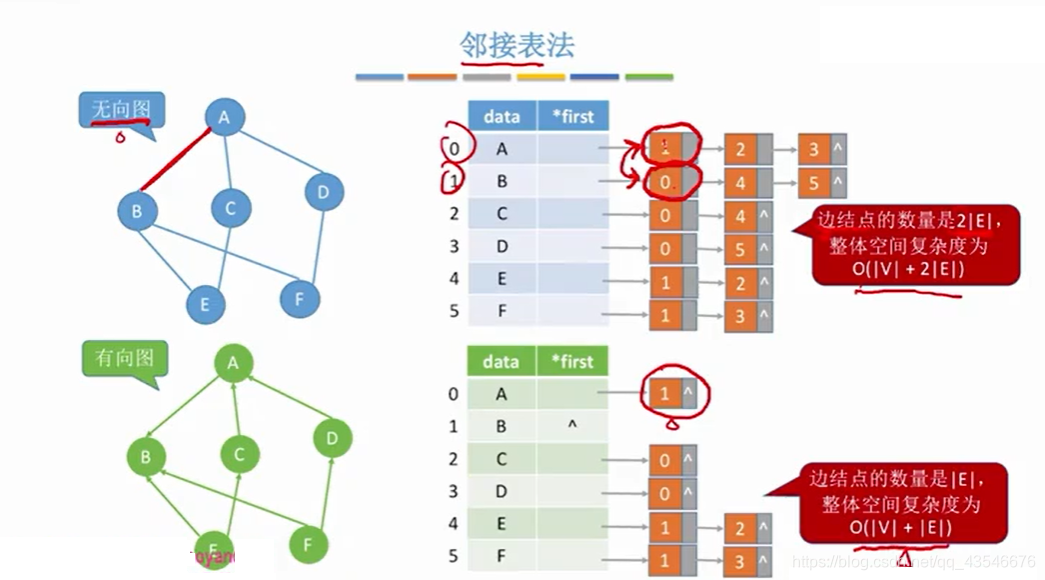
那么如何计算结点的度?
对于无向图来说,直接遍历某个结点的链表,链表的结点个数就是该结点的度数。
对于有向图来说,计算出度很简单,和无向图一样,但是求入度比较麻烦,需要遍历各个结点的链表才能知道。
另外,由于每个结点的链表的结点无顺序关系,导致每个图的邻接表不唯一。但是,一个图的邻接矩阵是唯一的。
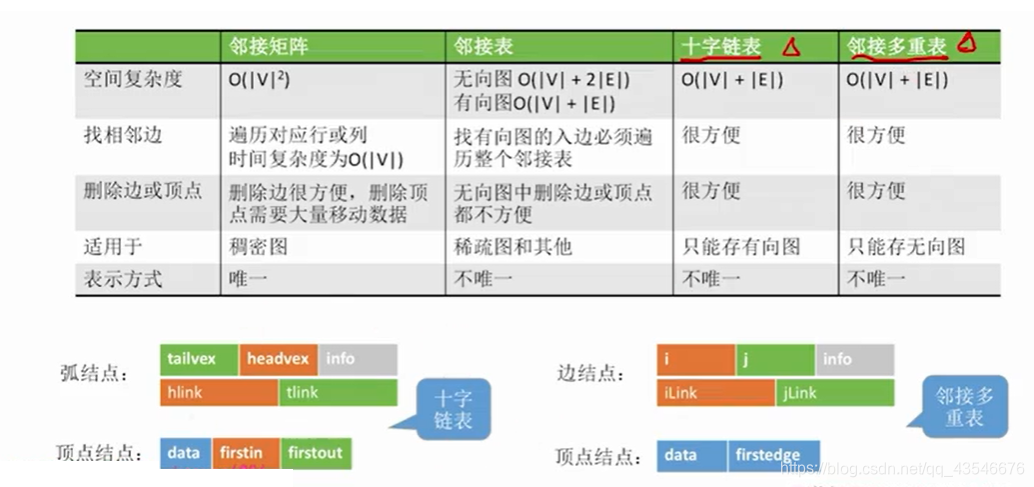
2.3 邻接表与邻接矩阵对比

2.4 十字链表法(有向图)
2.4.1 十字链表法
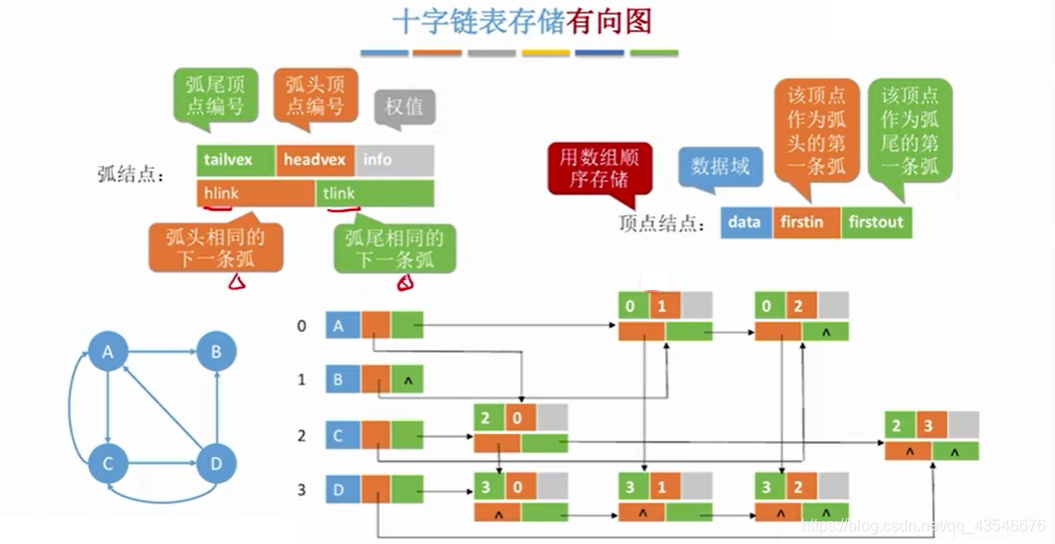
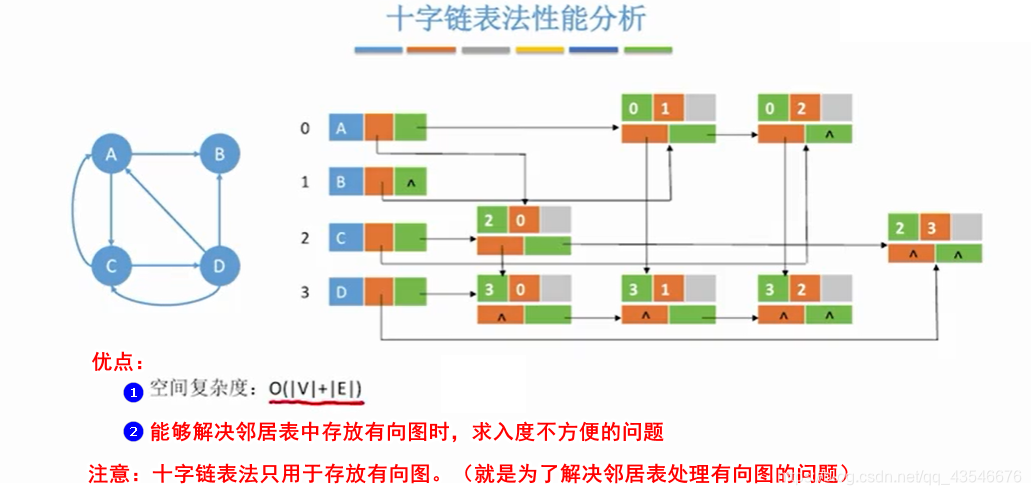
2.4.2 性能分析
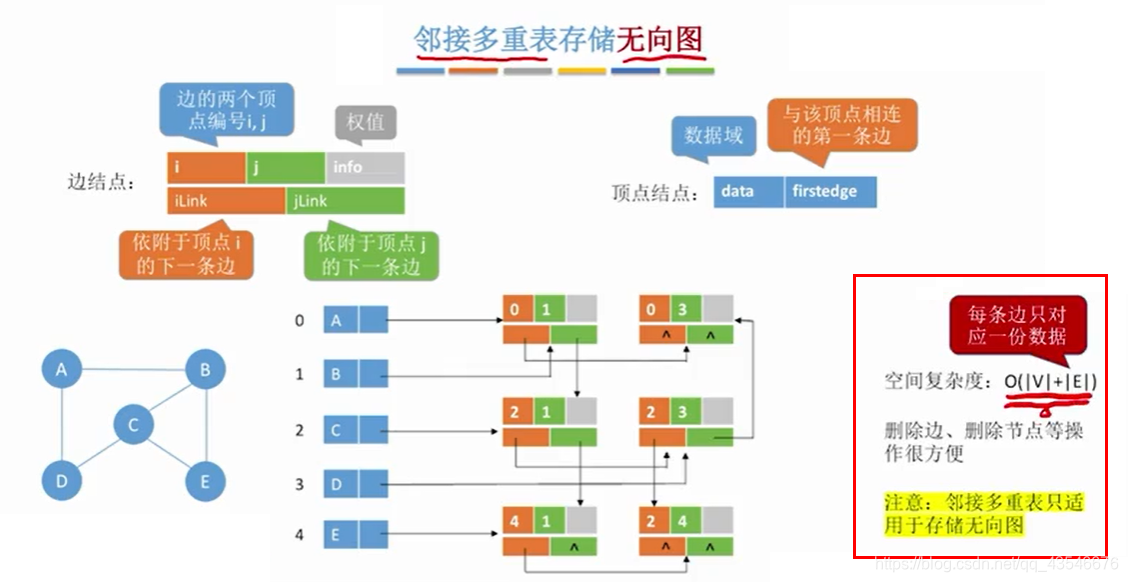
2.5 邻接多重表法(无向图)
对于无向图的存储,如果使用邻接矩阵的方法,会导致空间复杂度高;如果使用邻居表法,会导致有冗余边被存储,且删除顶点边很麻烦。
邻接多重表法可以解决以上问题。
2.6 小结
3. 基本操作

4. 图的遍历
* 图的遍历:访问所有顶点,且每个顶点只被访问一次。
* 注意:这个说法是错误的:从某一个顶点出发访遍图中其余顶点。
原因:第一是每个结点只能被访问一次,第二是如果是非连通图,从一顶点出发是无法访问所有结点的。
* 分类:
1. 广度优先遍历(BFS)
2. 深度优先遍历(DFS)
4.1 广度优先遍历(BFS)
4.1.1 算法思想

图的广度优先算法只是比树的层次遍历多了一步:在添加邻接结点的时候,先判断该邻接结点是否被访问过,若访问过则不入队列,反之入队列。
还需要注意一点的是,得到某节点的邻接结点时,一般是for(int i = 0; i < 数组长度; i++),下标从小到大,所以某结点有多个邻接结点时,是下标小的结点先入队。
4.1.2 代码实现
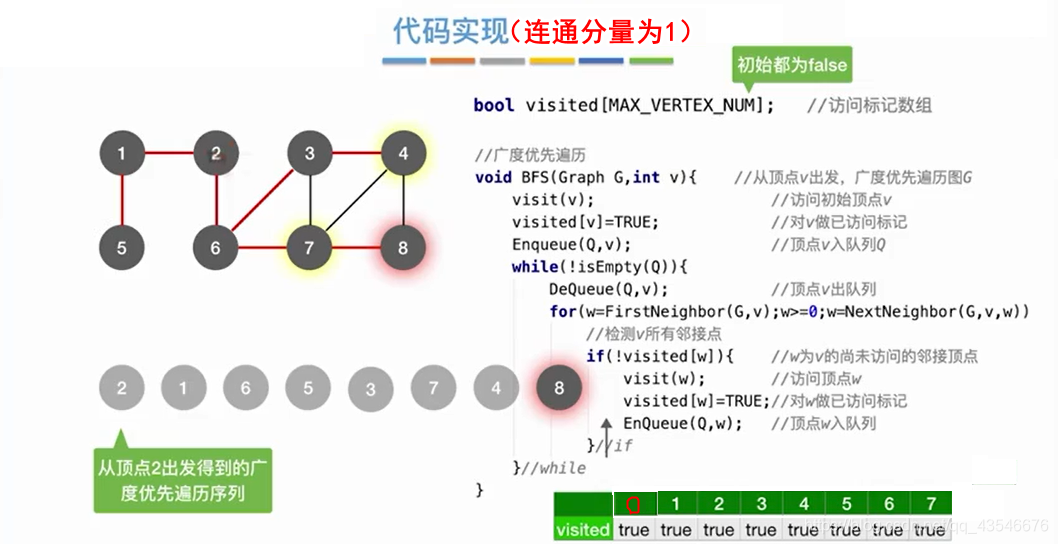
注意:由于邻接矩阵表示唯一,所以用邻接矩阵得到的广度优先遍历唯一。邻接表的表示不唯一,所以用邻接矩阵得到的广度优先遍历不唯一。
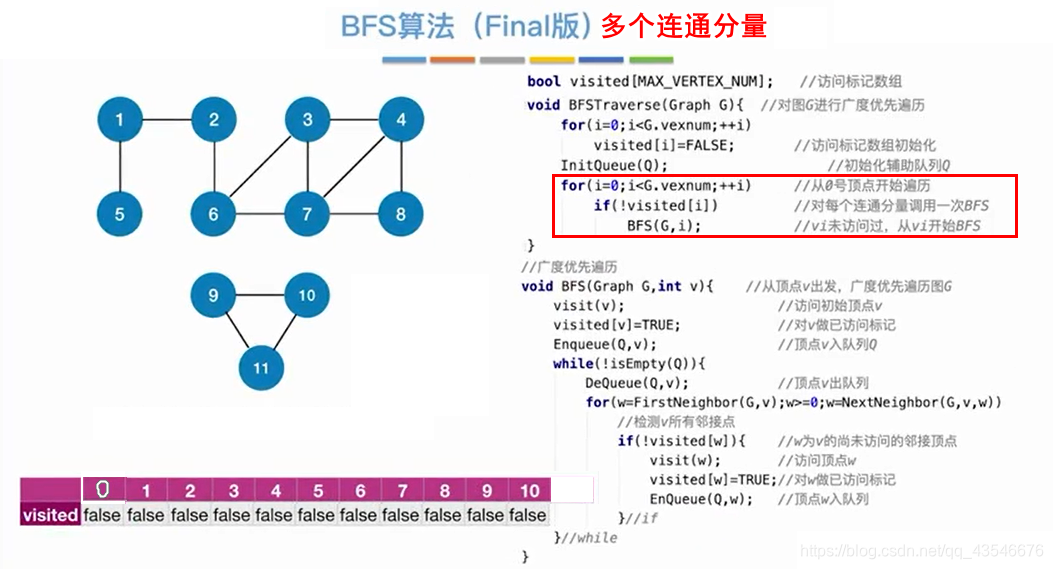
多个连通分量,则只需要在外面套个for循环就可以了。调用BFS函数的次数等于连通分量的个数。
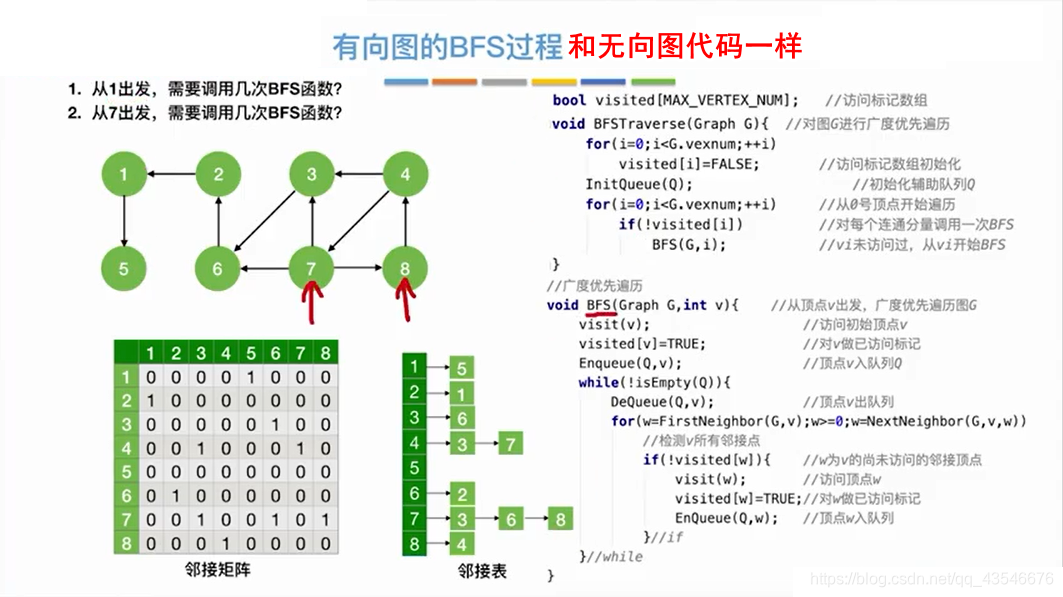
有向图调用BFS函数的次数要根据具体情况确定。
4.1.3 性能分析
对图和树的遍历,时间复杂度都来自于对边和结点的访问,所以在求广度优先遍历的时候,我们只需要求访问边和结点的次数就可以了。
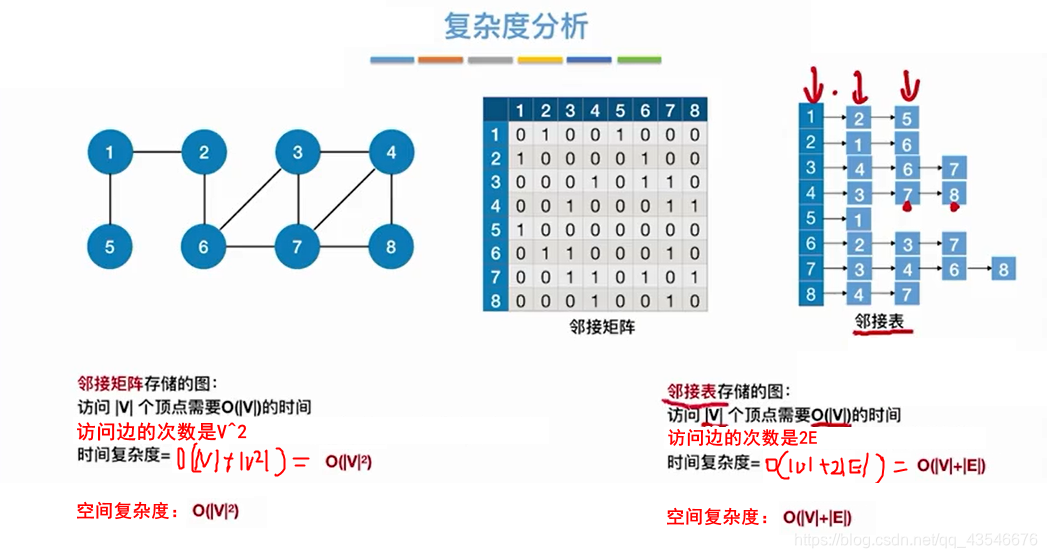
辅助队列最坏大长度是O(|V|)
4.1.4 广度优先生成树
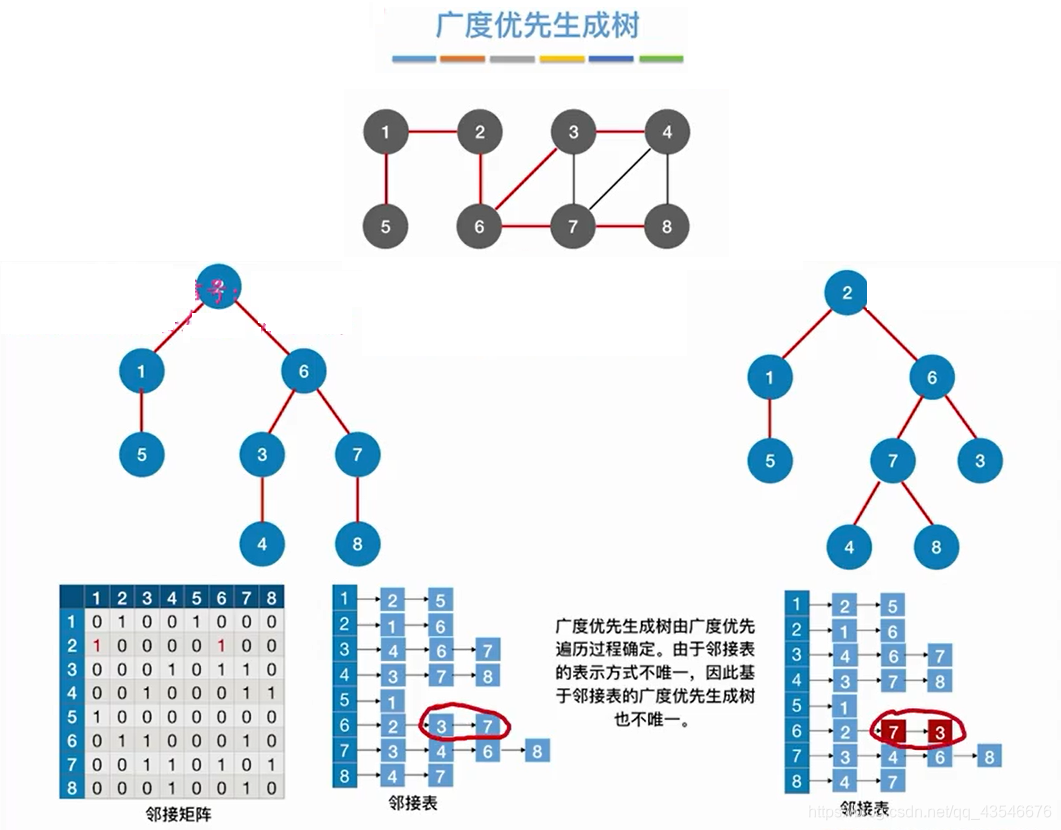
实现算法的核心就是:在广度优先遍历的基础上,加一步,即在弹出该结点之后,该结点的邻接结点入队之前,将邻接结点添加为该结点的孩子结点。
注意:由于同一图的邻接矩阵唯一,所以其广度优先遍历唯一,导致其广度优先生成树唯一;而同一图的邻接表不唯一,所以其广度优先遍历不唯一,导致其广度优先生成树不唯一。
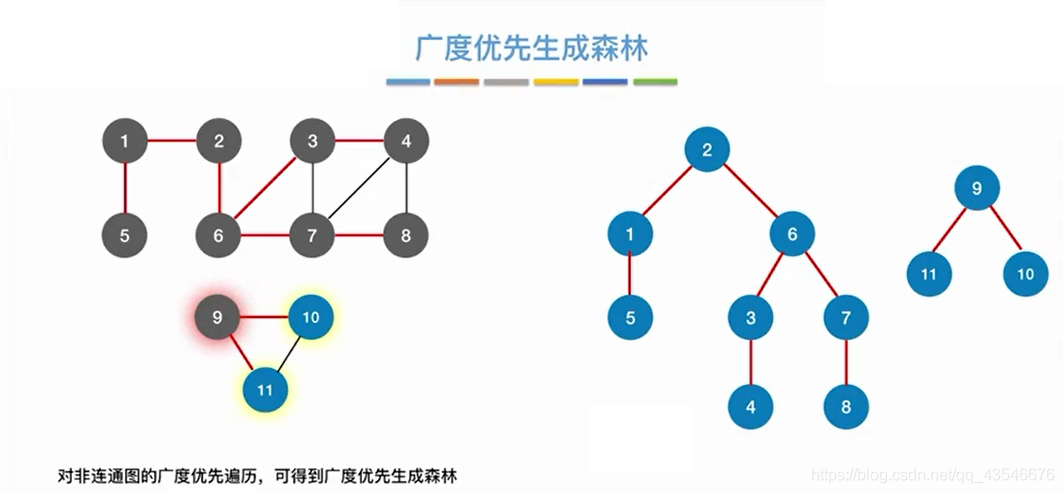
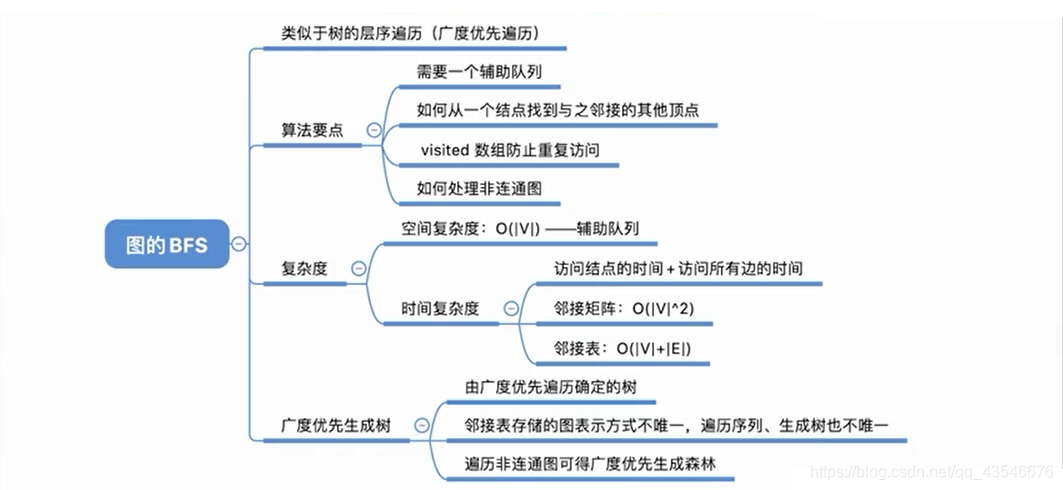
4.1.5 小结
4.2 深度优先遍历(DFS)
4.2.1 算法思想
DFS的思想和树的先根遍历/后根遍历的思想是一样的,只是和BFS一样加了一个visited数组,防止死循环。一般取与树的先根遍历相同的思想实现DFS。
注意:在做题时,默认DFS为先根遍历
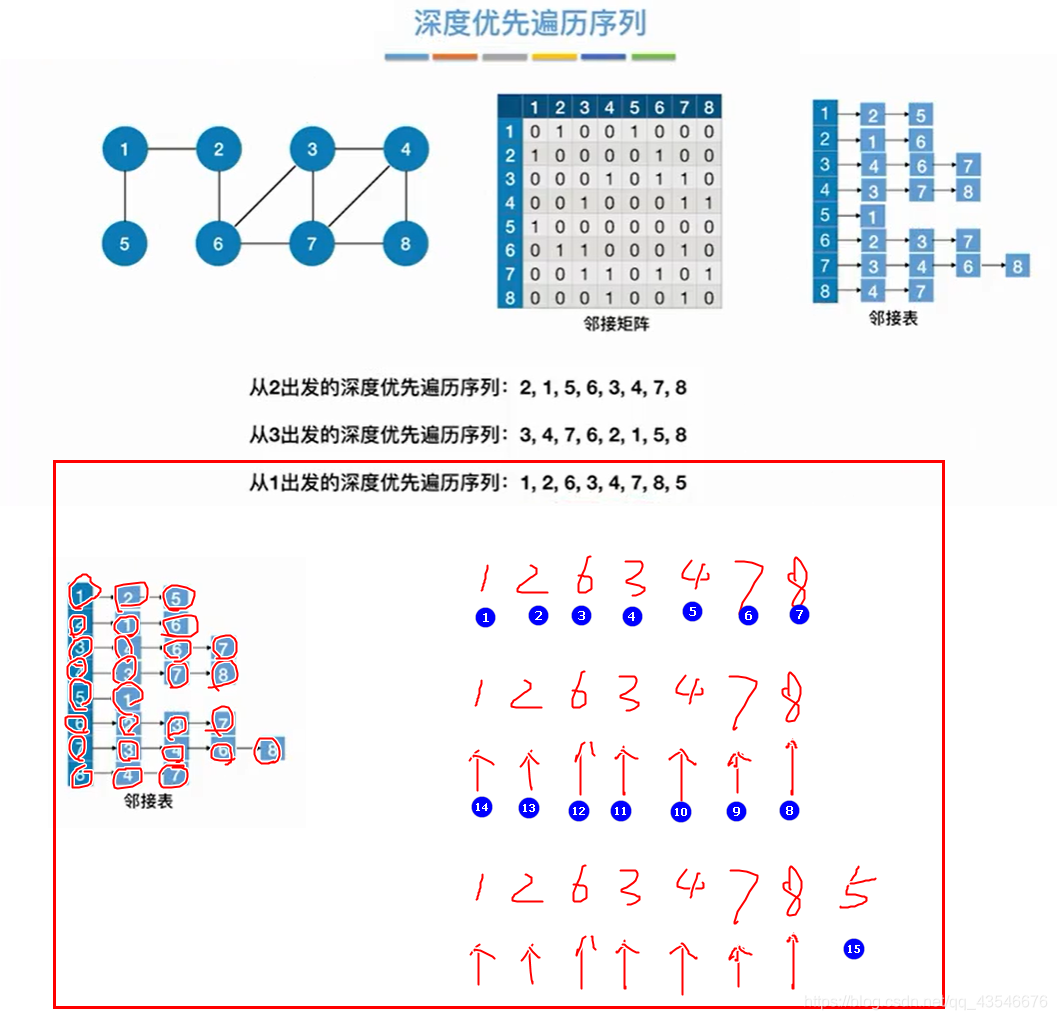
4.2.2 代码实现
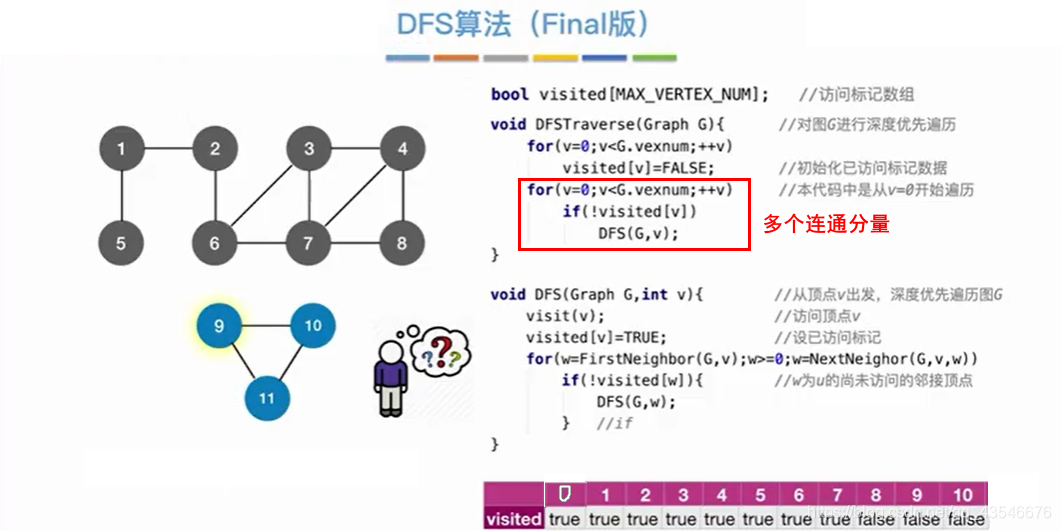
注意:和BFS一样,由于邻接矩阵表示唯一,所以用邻接矩阵得到的深度优先遍历唯一。邻接表的表示不唯一,所以用邻接矩阵得到的深度优先遍历不唯一。
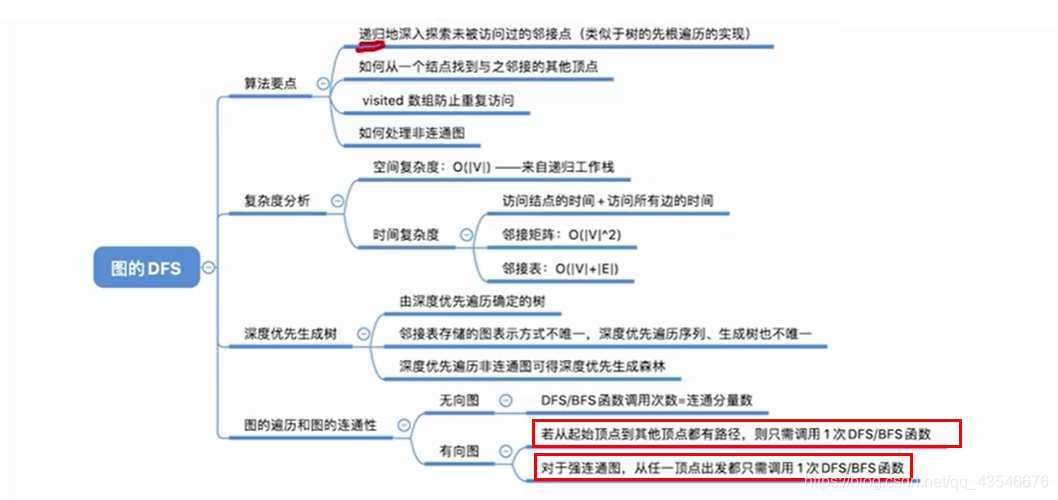
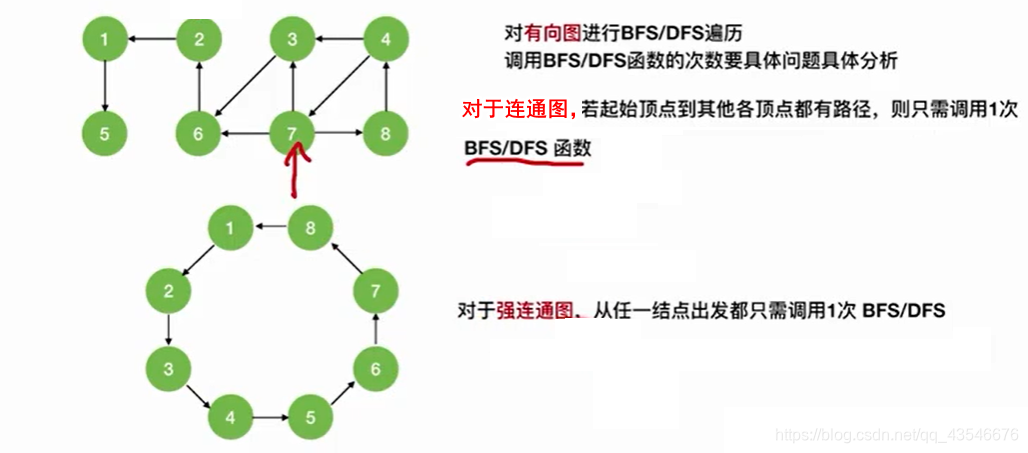
有向图的DFS代码和无向图一样,有向图调用DFS函数的次数和连通分量个数一样,有向图调用DFS函数的次数要根据具体情况确定。
4.2.3 性能分析
和BFS类似,在求DFS的复杂度时,我们只需要求访问边和结点的次数就可以了。并且,其空间复杂度以及时间复杂度都和BFS一模一样。
4.2.4 深度优先生成树
深度优先生成树与广度优先生成树非常类似,都是基于其遍历的基础上。
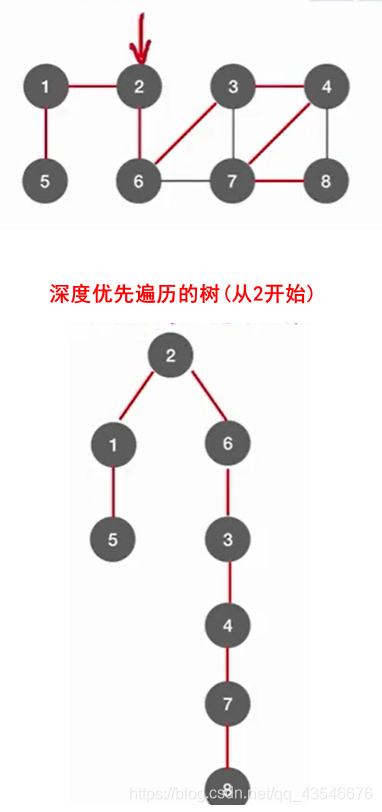
森林就是每个连通分量都深度优先遍历生成深度优先生成树。和BFS类似。
4.2.5 小结
5. 图的最小生成树
5.1 最小生成树概念
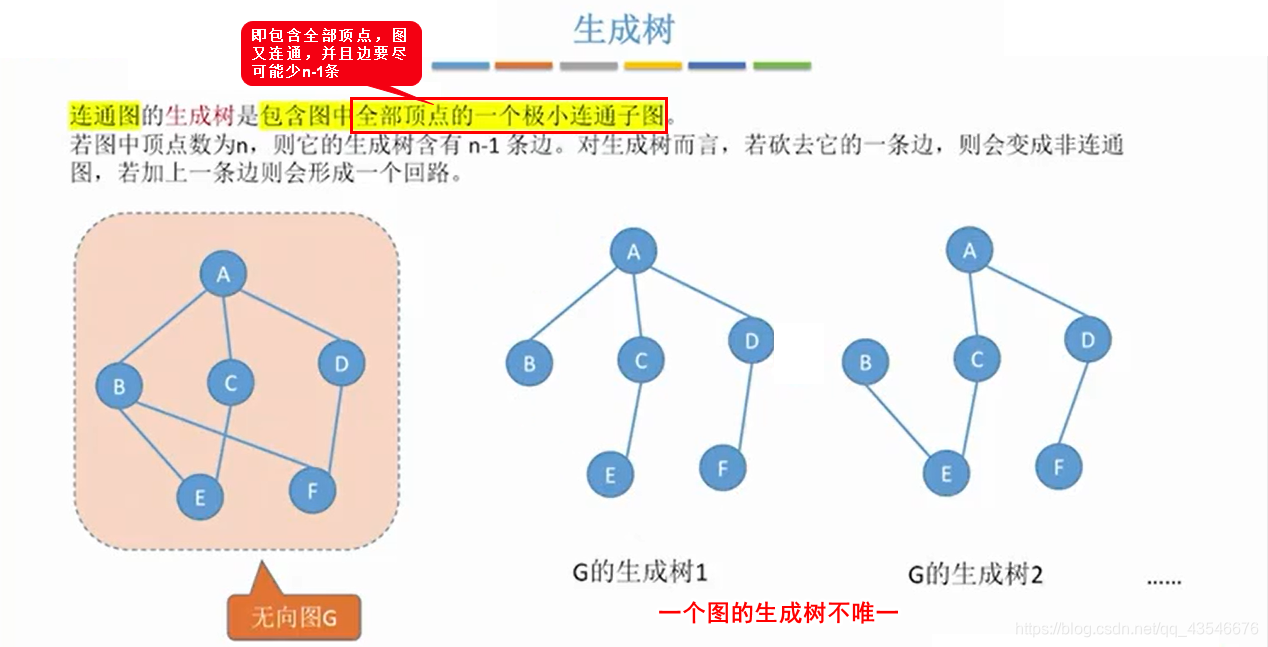
最小连通图:指该图的所有生成树中,各条边权值之和最小的那个数。(强连通图和连通图都是一颗或多棵最小生成树不唯一,多颗是有权值相等导致,一颗是指强连通图和连通图的最小生成树必定存在)
如果该图本就是一棵树(即不存在环路), 则其最小生成树就是他本身。
连通图有最小生成树,非连通图有最小生成森林。
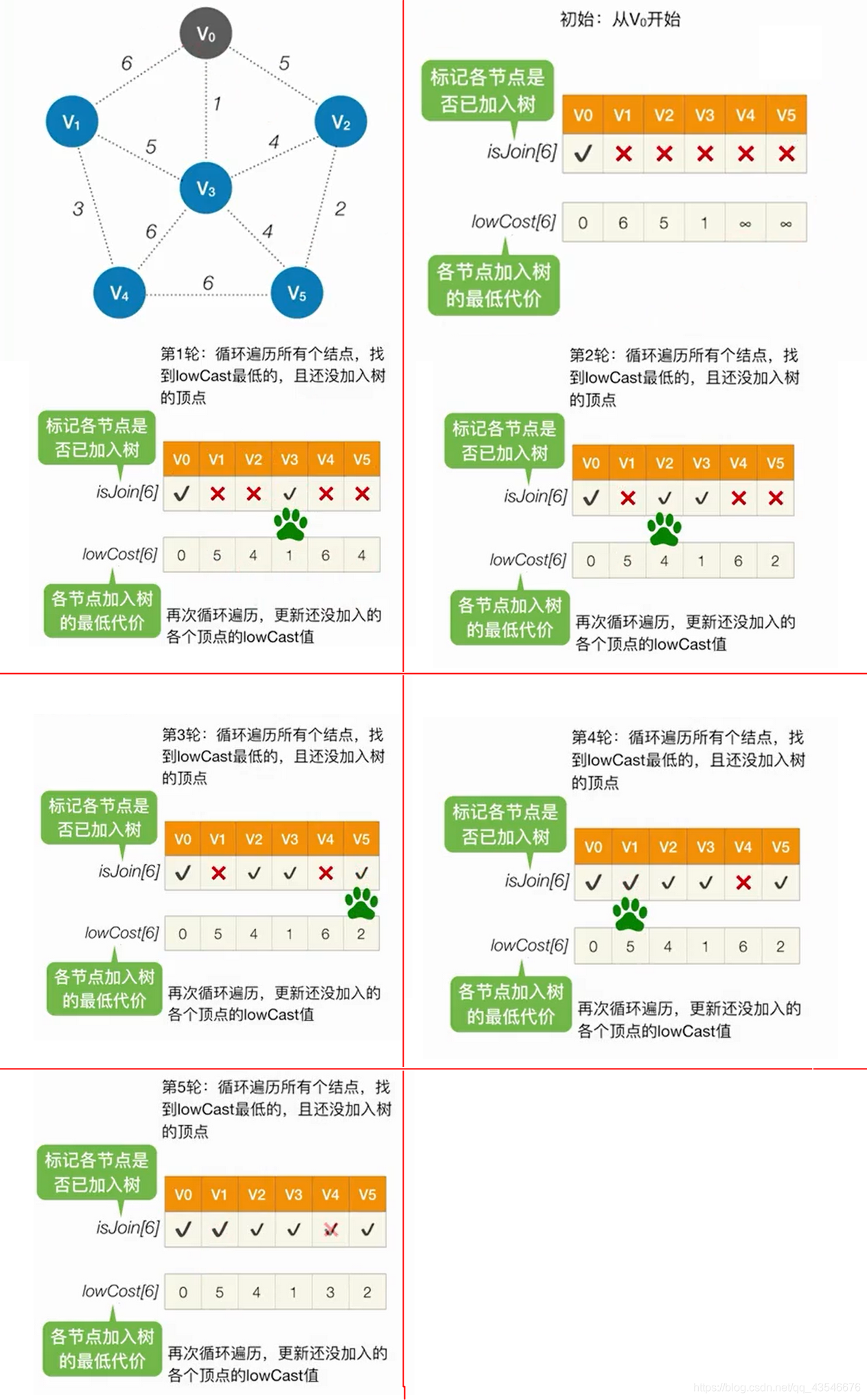
5.2 Prim算法构成最小生成树
算法过程:
- 初始时,从图中任意取一个点加入集合T
- 选择离T中顶点集合最近的顶点,将该顶点和相应的边加入集合T,每次操作后T中的顶点数和边数都加1
- 重复上面过程,直到所有顶点都加入到T中
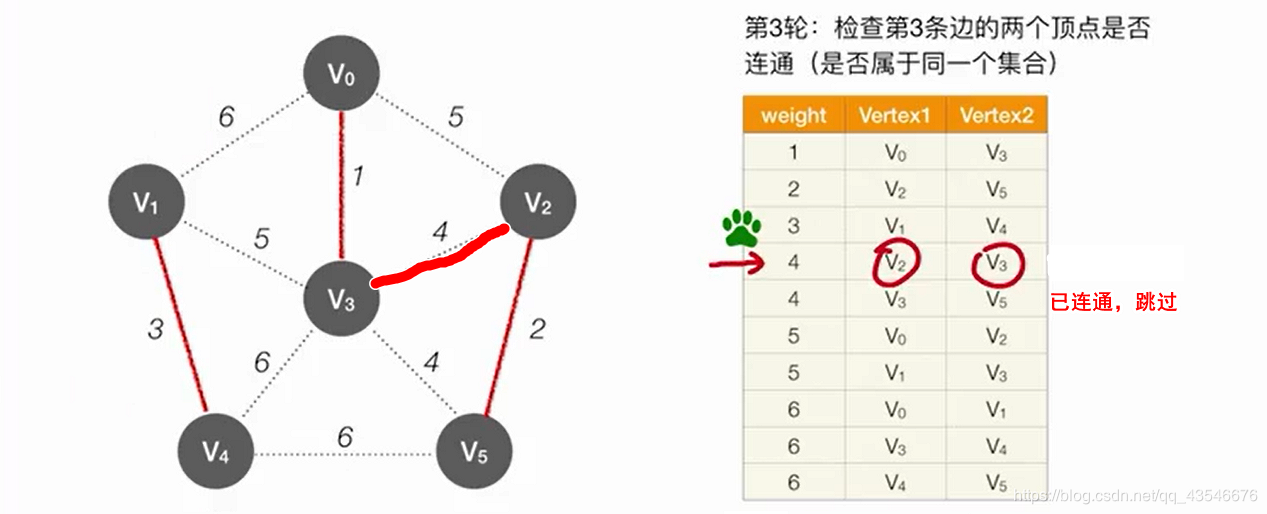
5.3 Kruskal算法构成最小生成树
算法过程:每次选择一条权值最小的边,有三种情况:
- 如果两条边的两头不在任意一个独立集合,则使这两条边的两头连接,组成一个独立集合T;
- 如果连接的两个顶点只有一个在独立集合中,则将另一个顶点和相应边加入该独立集合中
- 如果连接的两个顶点在不同的独立集合,则将这两个独立集合合并,表示将两个子图连通
5.4 小结

注意:Prim和Kruskal的算法复杂度很相近,但是细的来说,还是Kruskal的算法复杂度更优。
6. 最短路径
* 最短路径类别
1. 单源最短路径:指从某个结点结点出发,能够求从该结点到其他任意结点间的最短路径。
* 算法
1. BFS算法实现(只适用于不带权的图)
2. Dijikstra算法实现(带正权图/无权图都行)
2. 各顶点间的最短路径:能够求任意两个结点间的最短路径。
* 算法
1. Floyd算法实现(带权图/无权图都行)
2. BFS和Dijikstra也能实现。只需要在其算法的外部再嵌套一个循环,这样从每个结点的单源最短路径就变成了各顶点间的最短路径。
* 注意:最小生成树是整体最小,而最短路径是顶点间路径最小。
6.1 单源最短路径
6.1.1 BFS算法实现(只适用于不带权的图)
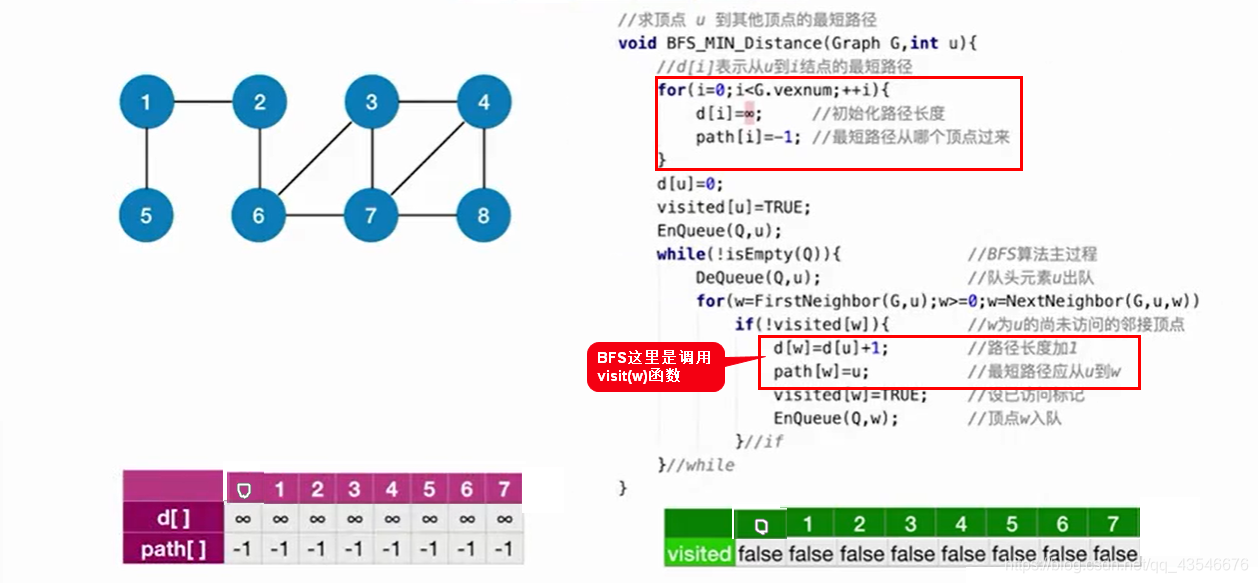
注意:算法复杂度为:O(|V^2|)

6.1.2 Dijikstra算法实现(带正权图/无权图都行)
若已V0为源,则集合为{V0}、{V1,V2,V3}
- 初始:dist[]数组放V0到V1,V2,V3的距离,path[]数组表示能从哪个结点来。
- 第一步:将V1加入{V0},变为{V0,V1}、{V2,V3},遍历dist[]数组,找到最小值的那个结点,即V4。再遍历dist[]数组,看从V0经过V1分别到达{V2,V3}的距离是否更短(dist[4]+从V4分别到{V2,V3}得到),如果更短则用该短值取代dist[]对应值。
- 第二步:将V2加入{V0,V1},变为{V0,V1,V2}、{V3}…一直重复操作,直到集合为空
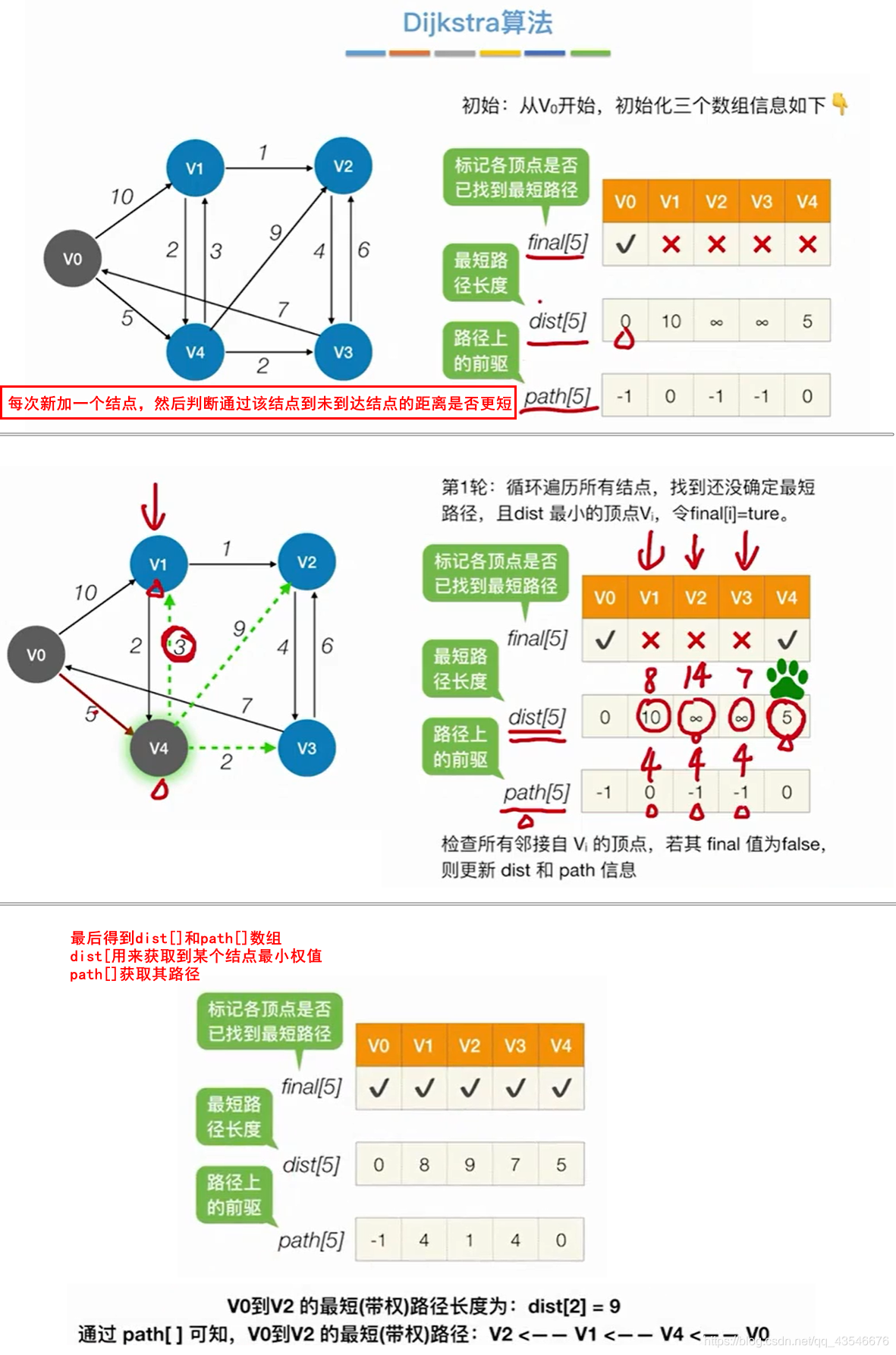
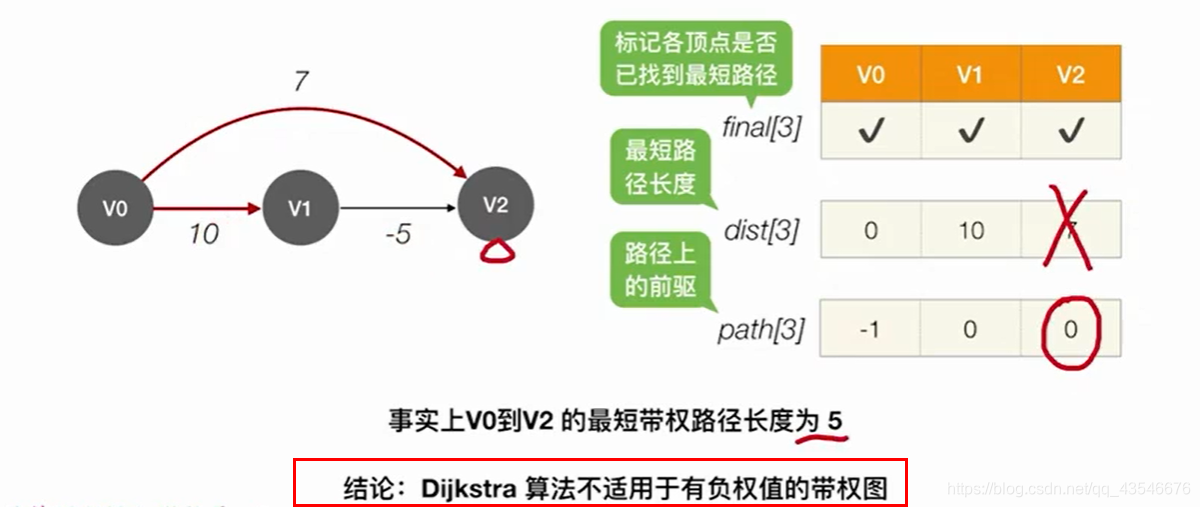
注意:Dijkstra算法不适用于带有负权值的图。
6.2 各顶点间的最短路径
首先,说明BFS和Dijikstra也能实现。只需要在其算法的外部再嵌套一个循环,这样从每个结点的单源最短路径就变成了各顶点间的最短路径。
接下来介绍另一种求各顶点间的最短路径的算法Folyd算法。
6.2.1 Folyd算法
6.2.1.1 算法思想

可以看见,其实Folyd的思想和Dijikstra思想非常的相似。
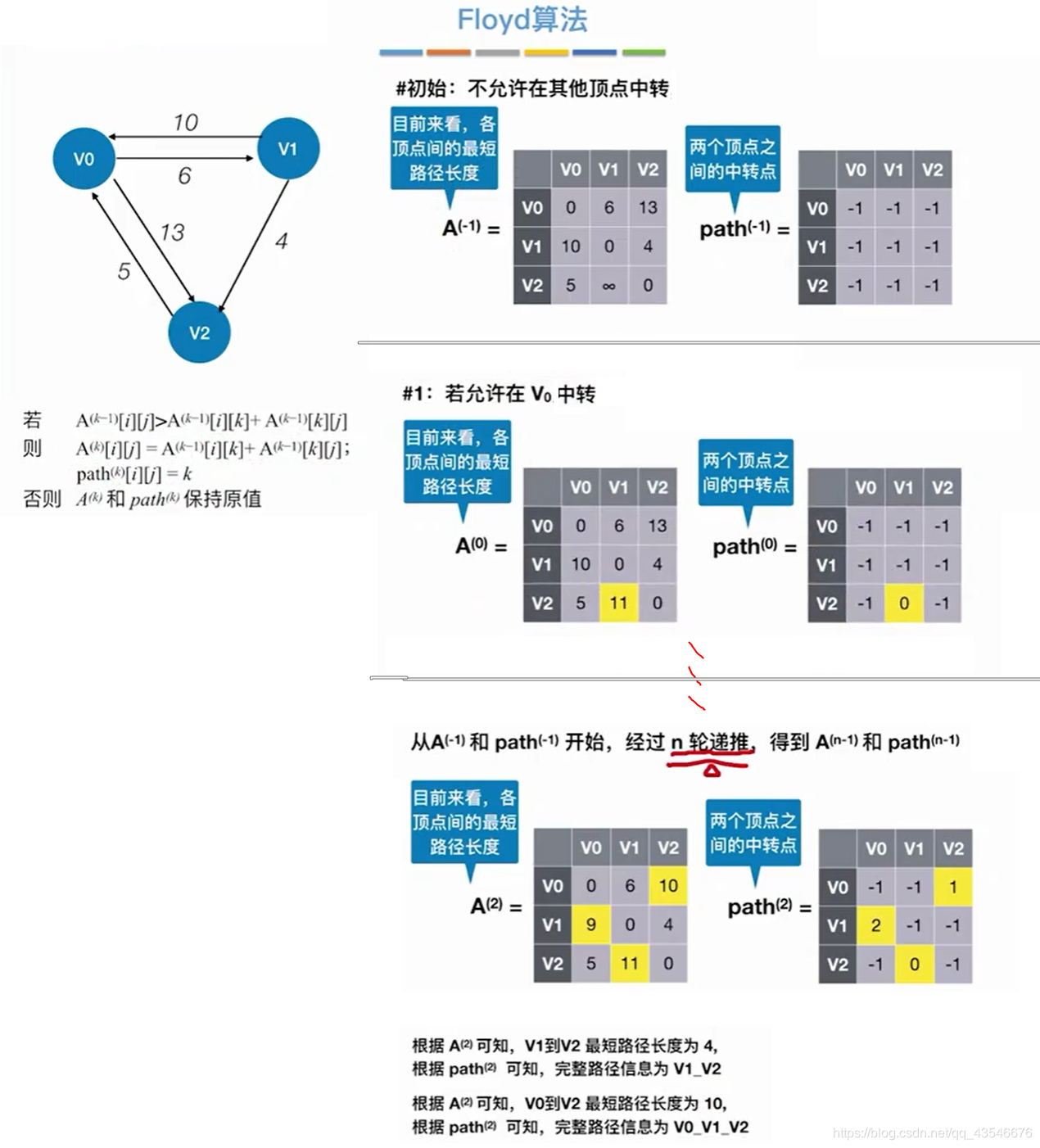
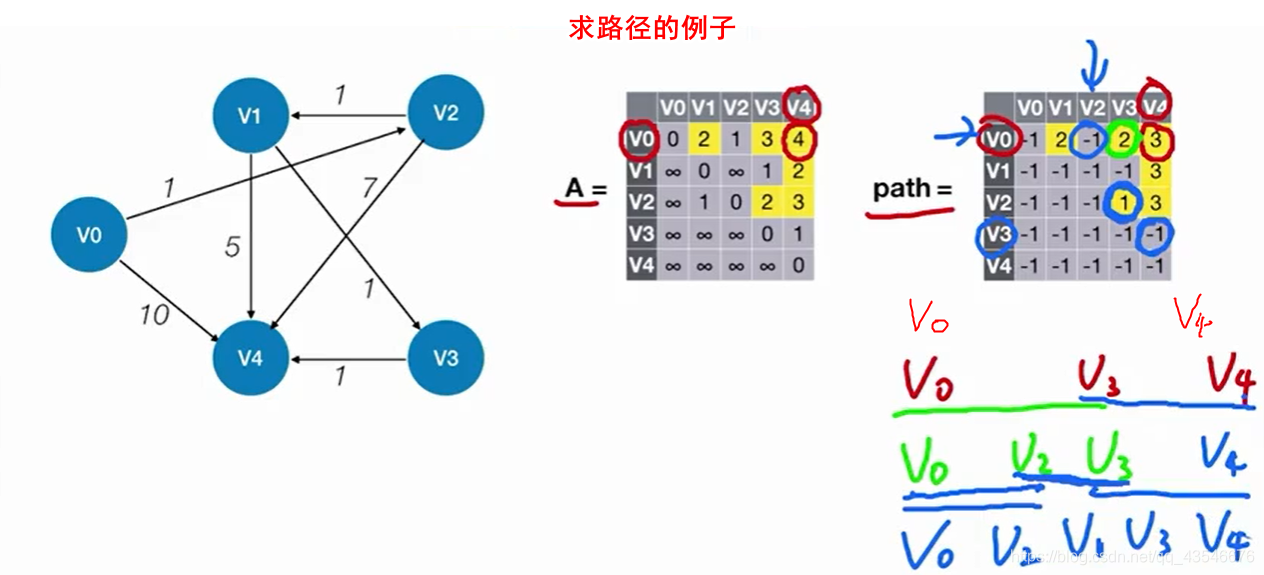
拿个简单例子练练手:
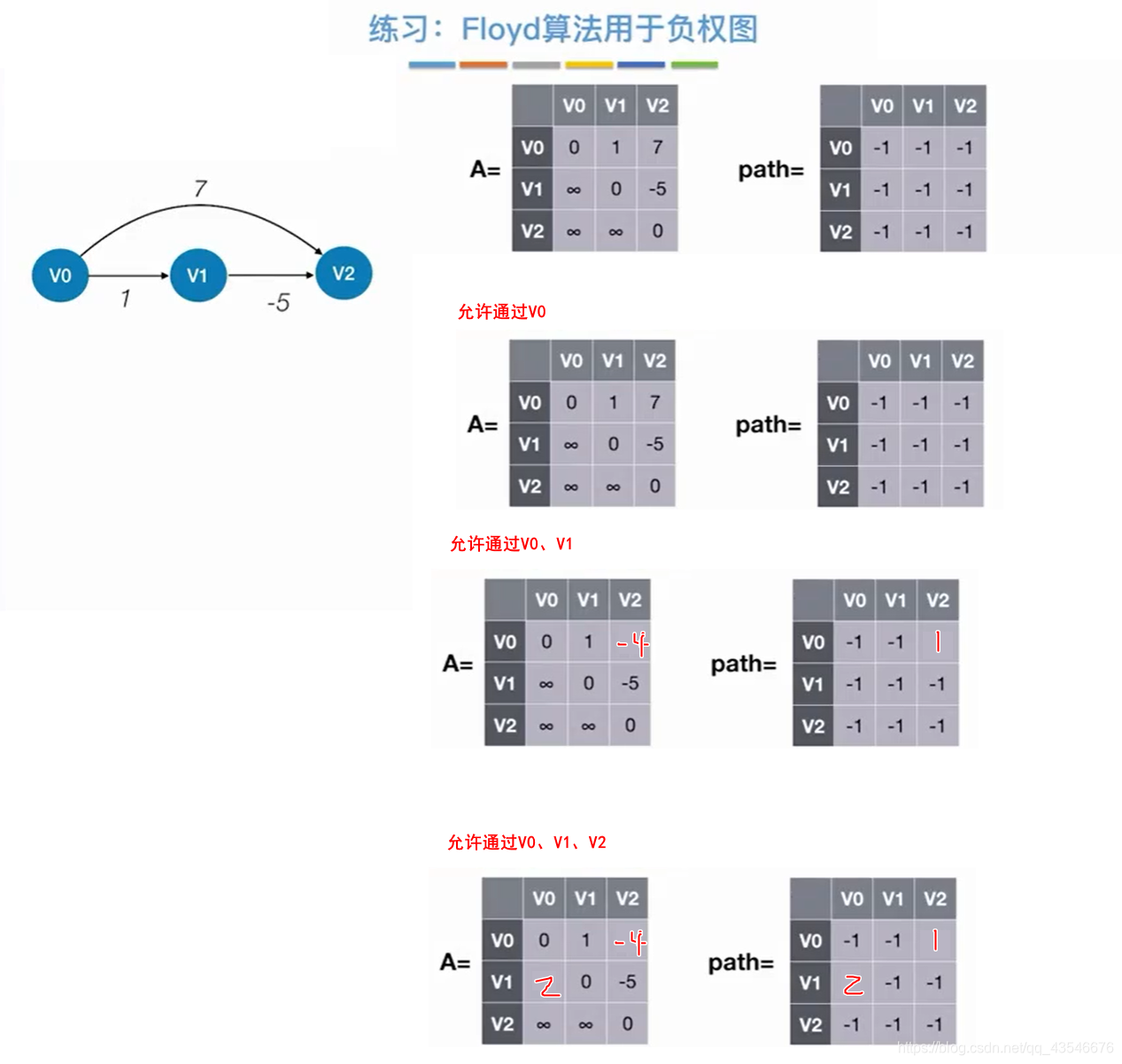
6.2.1.2 算法实现

6.2.1.3 Folyd算法缺点
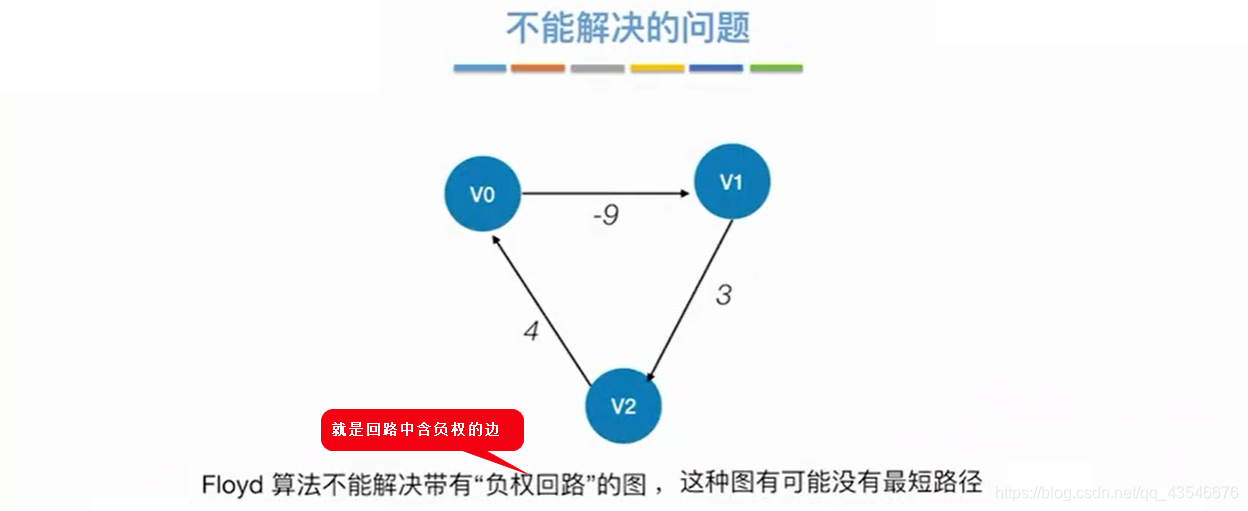
6.3 小结

注意:上面这三种方法都可以求带回路的连通图的最短路径,但是不能判断图是否有环。
7. 有向无环图
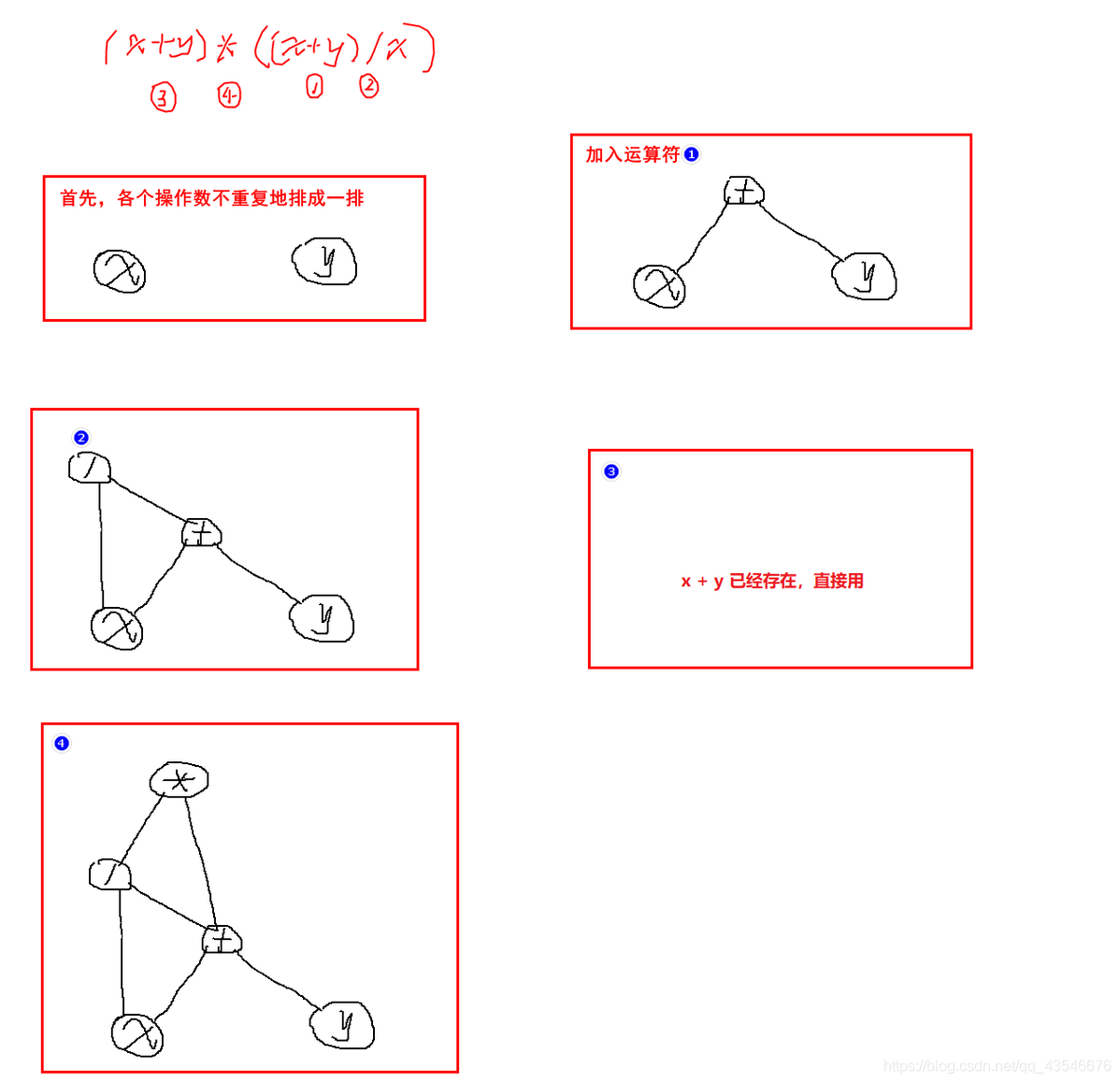
7.1 有向无环图描述表达式
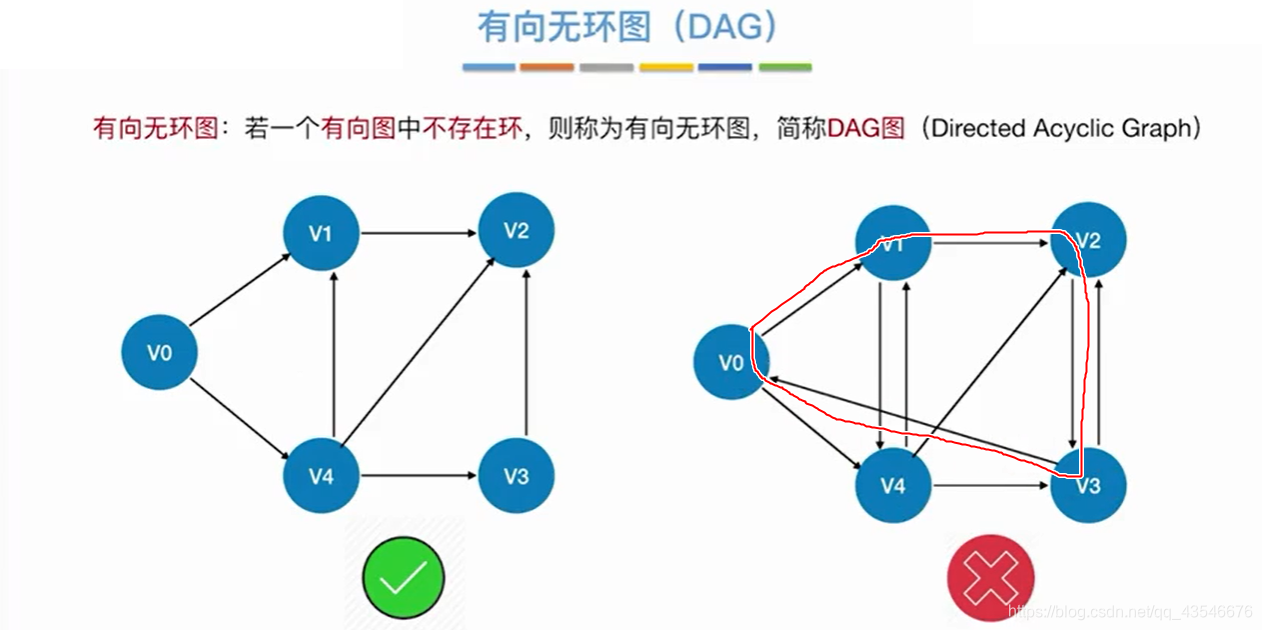
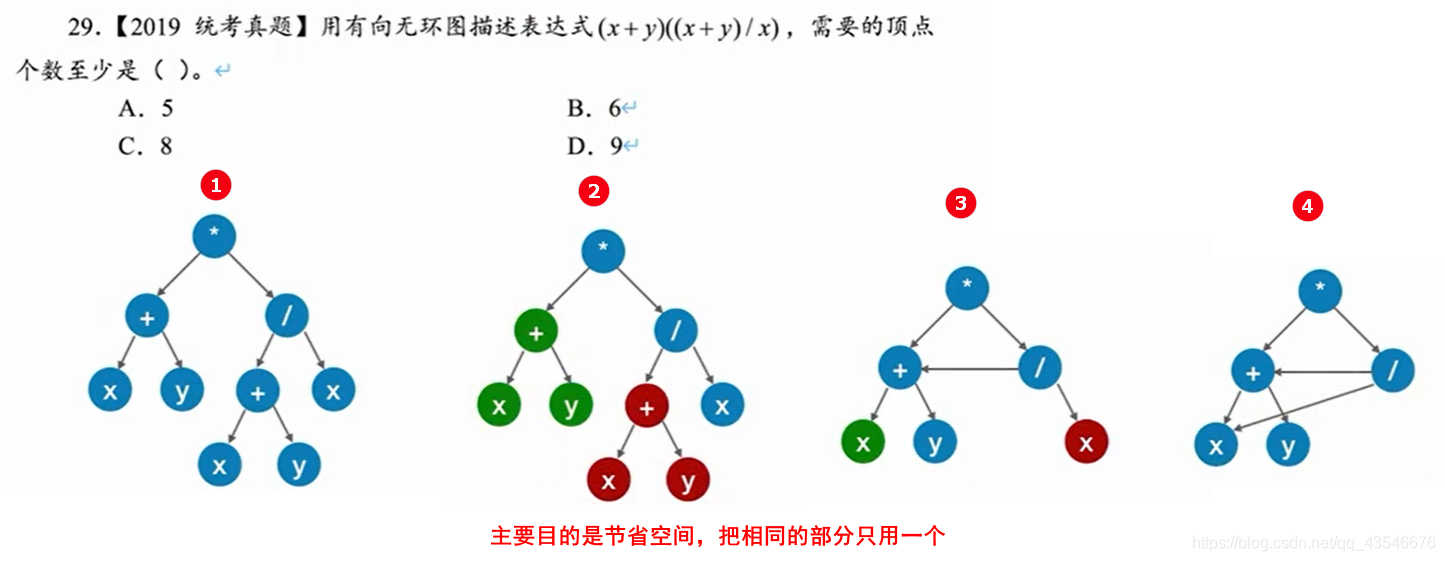
这样,比较混乱,如果式子一长,不容易看出来。
因此,按照如下步骤进行计算:
- 把各个操作数不重复地排成一排
- 标出各个运算符的生效顺序(先后顺序优点出入无所谓,比如先算左边括号或者先算右边括号,当然是同级的情况)
- 按顺序加入运算符,不同的运算级别层次不同,过程中如果已经存在某部分,则直接用
- 最后生成的图就是有向无环图
按照这个顺序,则上题应该这样做:

7.2 拓扑排序
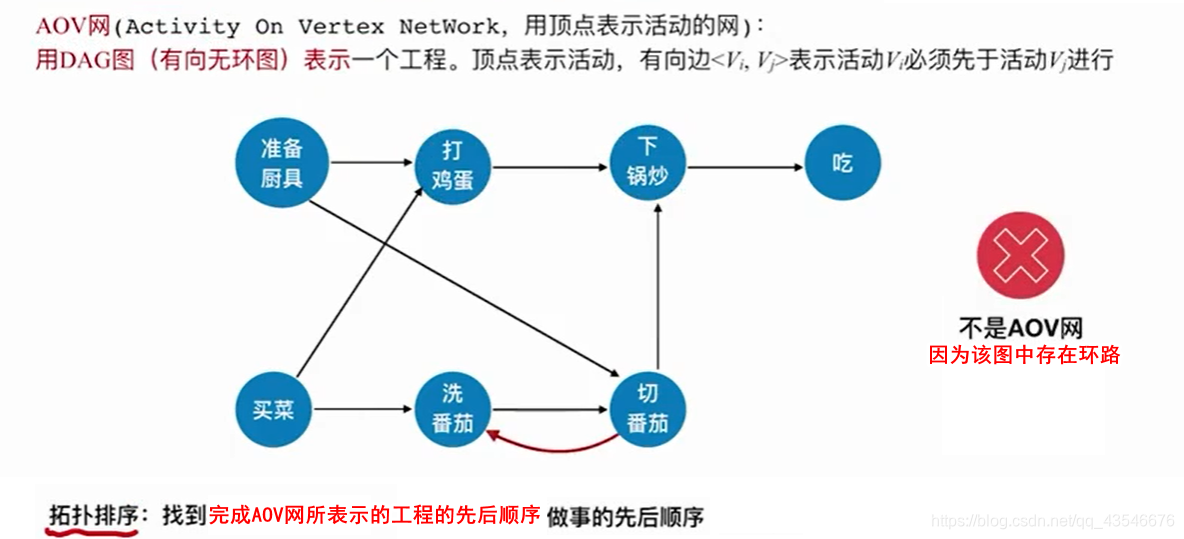
7.2.1 AOV网

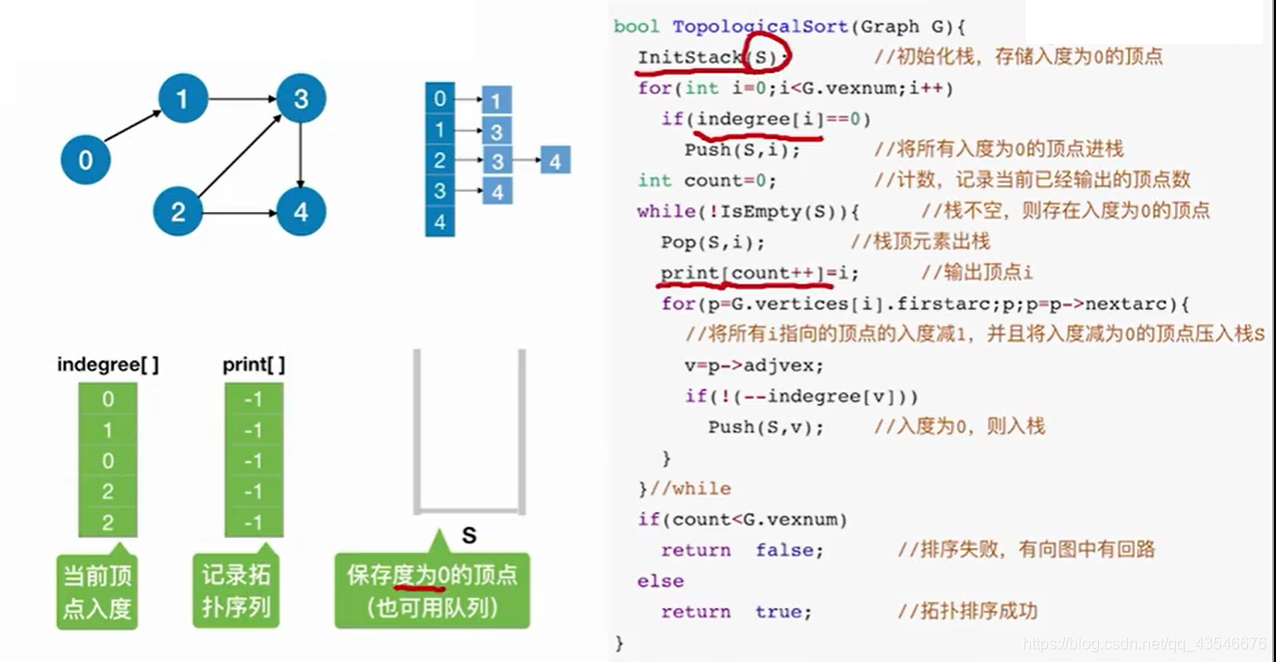
7.2.2 算法实现
7.2.3 算法复杂度

7.3 逆拓扑排序
逆拓扑排序和拓扑排序几乎一样,只是每次入栈的是出度为0的结点。

7.4 DFS(深度优先遍历)实现拓扑排序或者逆拓扑排序
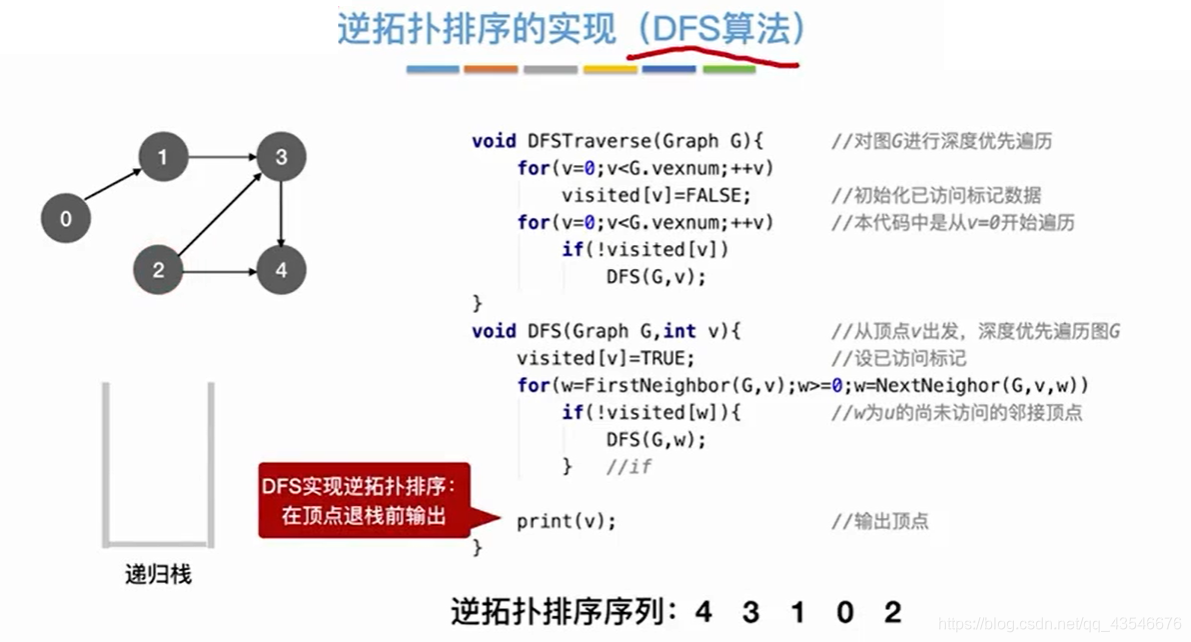
注意:这里是在退栈前打印顶点,所以是逆拓扑排序;如果是入栈时打印顶点就是拓扑排序。
7.5 小结
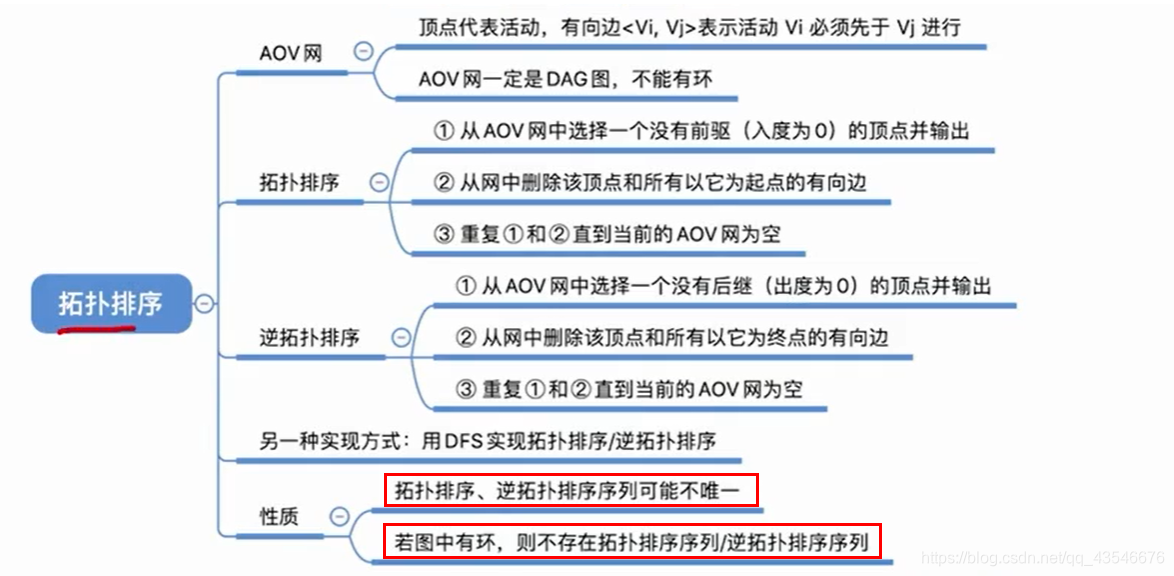
注意:拓扑排序中暂存度为0的结点可以用栈也可以用队列。
8. 关键路径
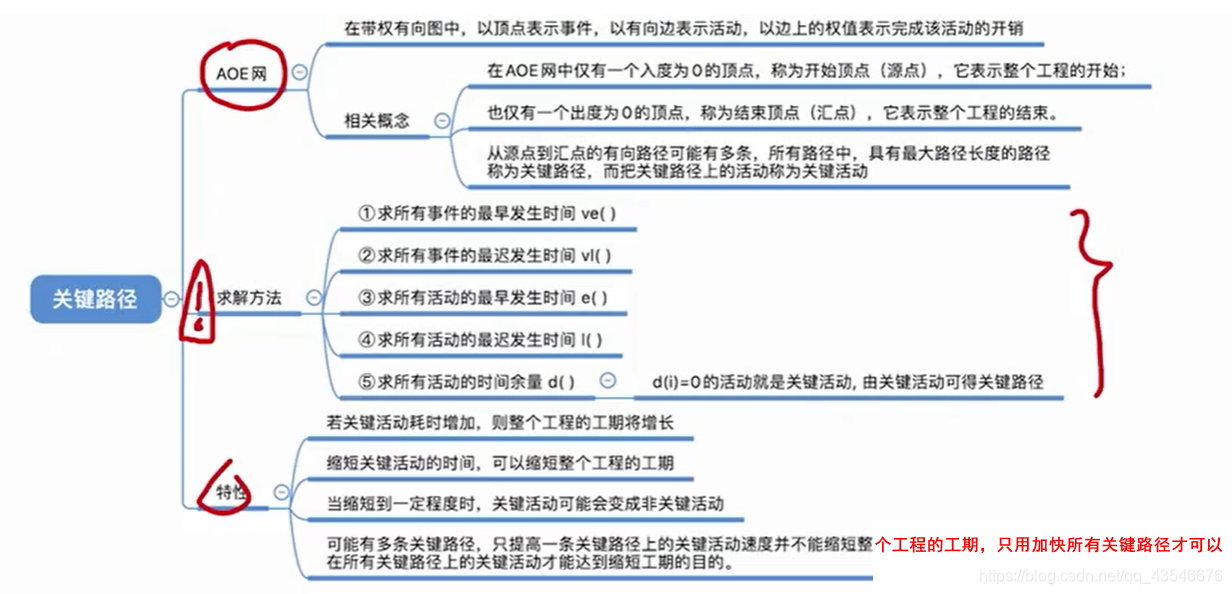
8.1 AOE网
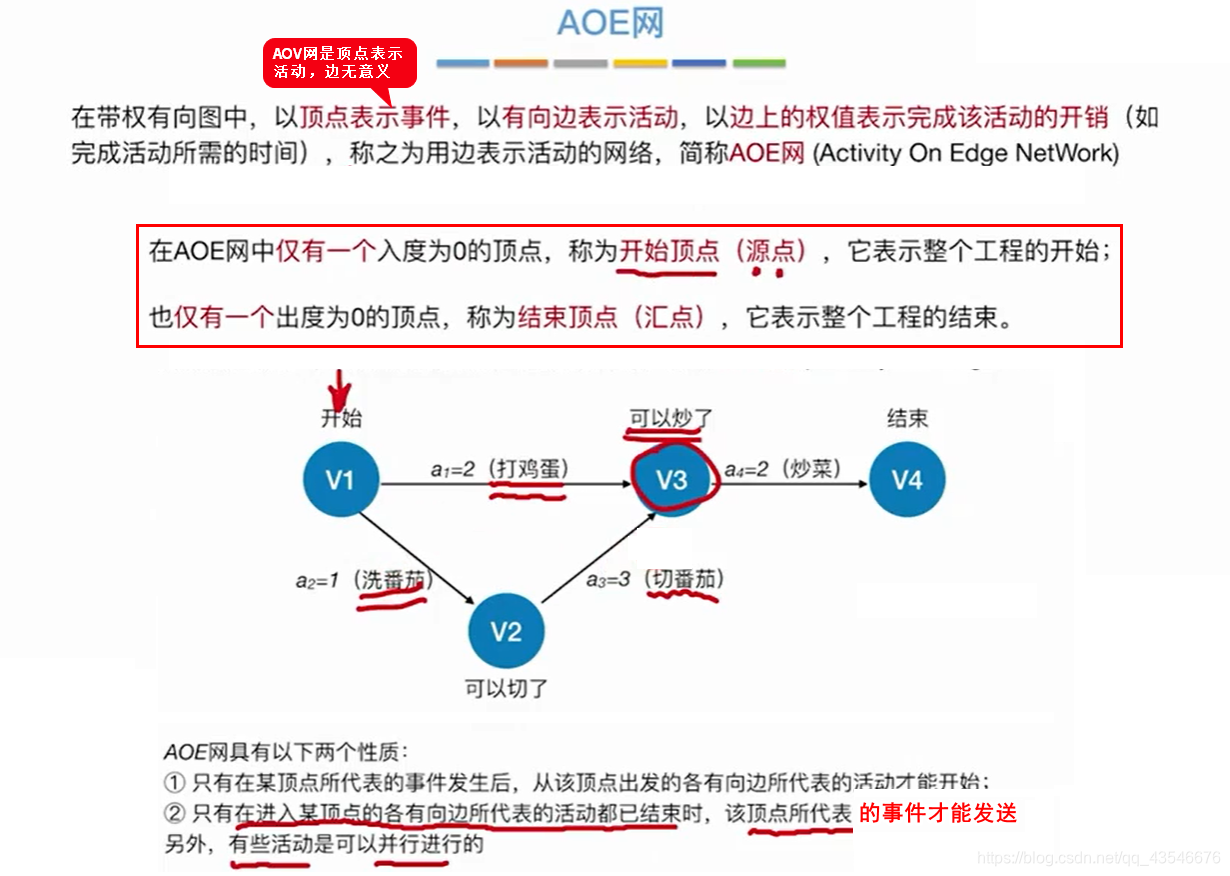
8.2 关键路径(最长路径)
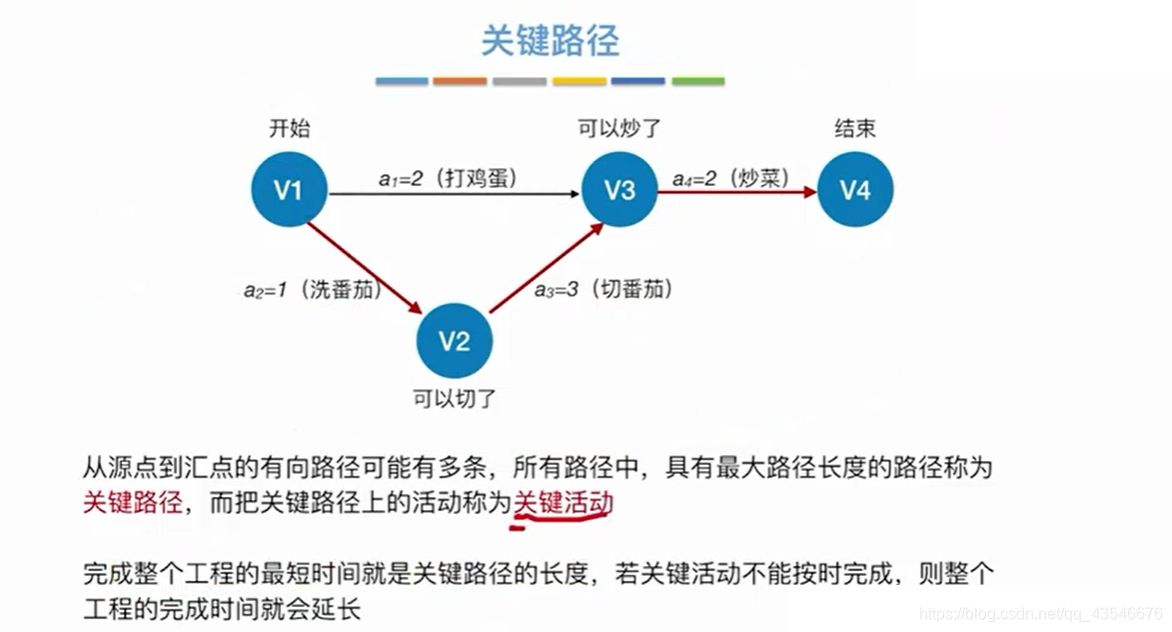

下面举一个求关键路径的例子:

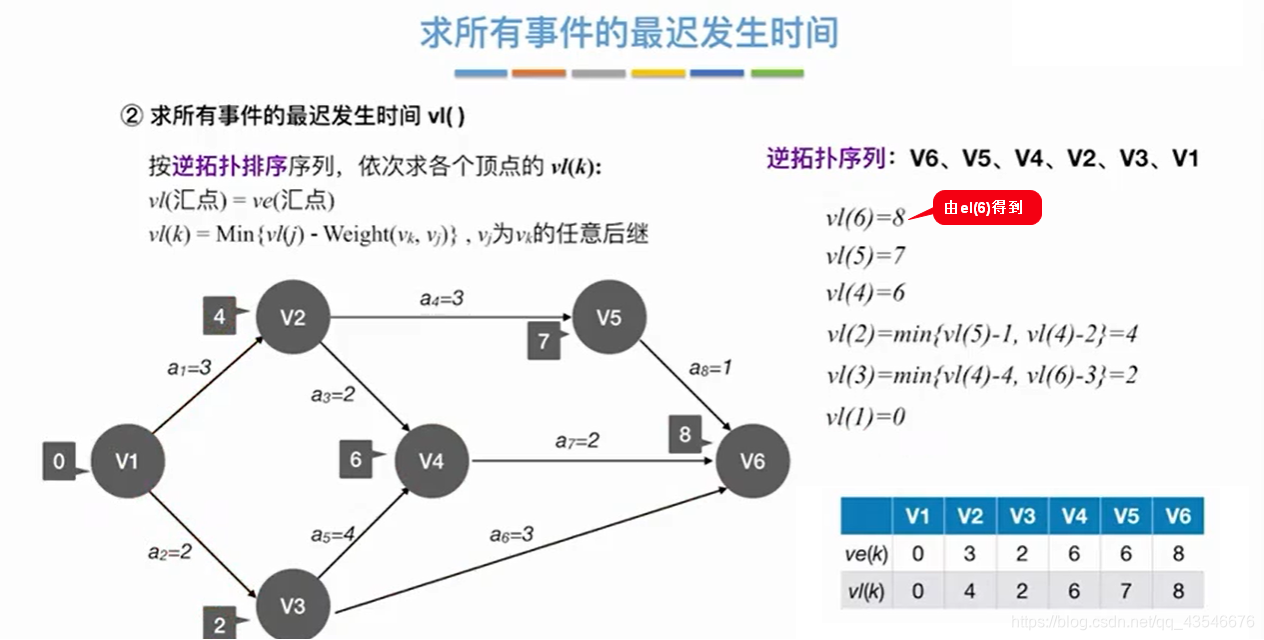

取箭头尾部的事件最早发生时间作为活动的最早发生时间。
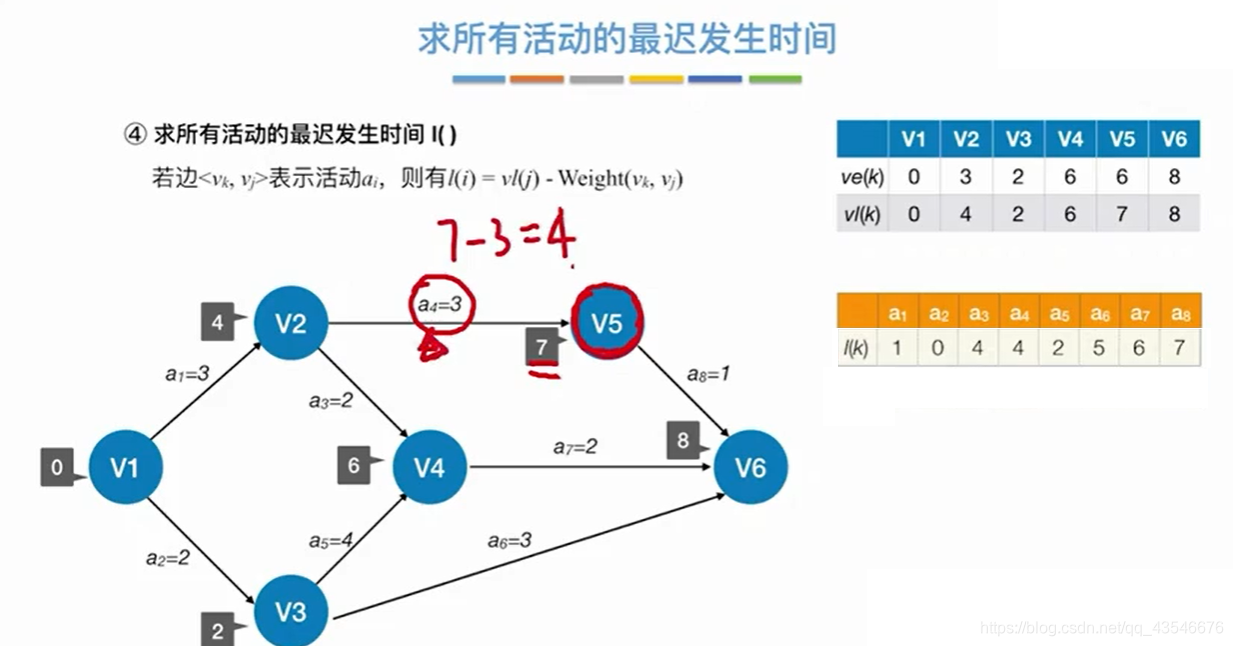
事件的最迟发生事件 - 相应的边 = 活动的最迟发生时间。
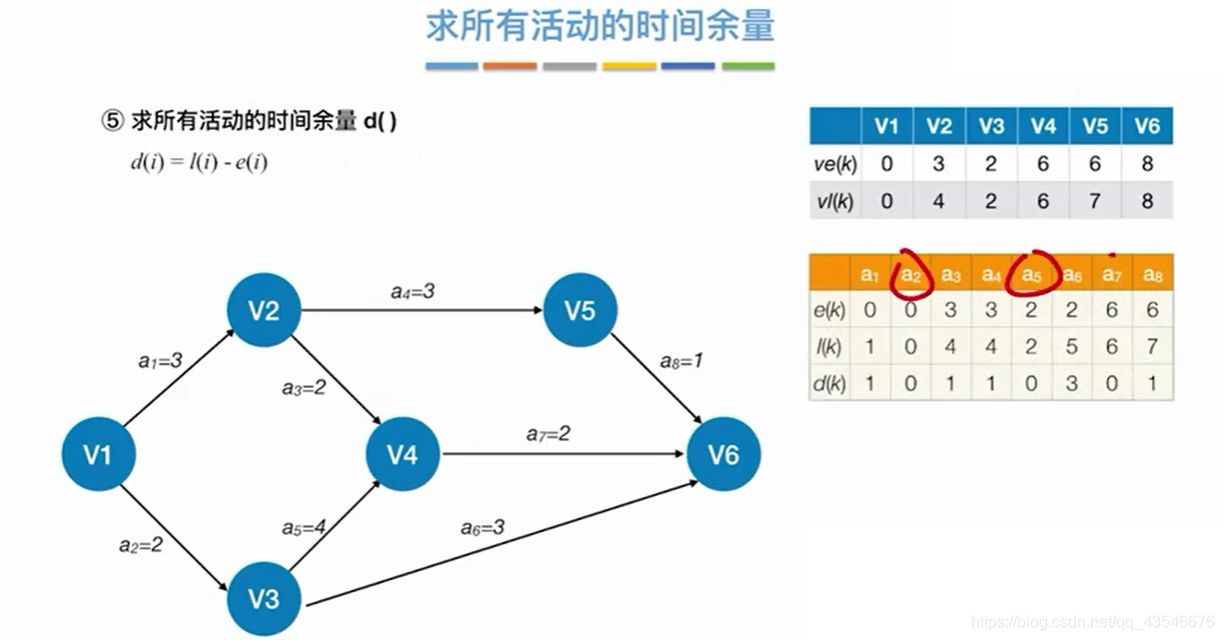
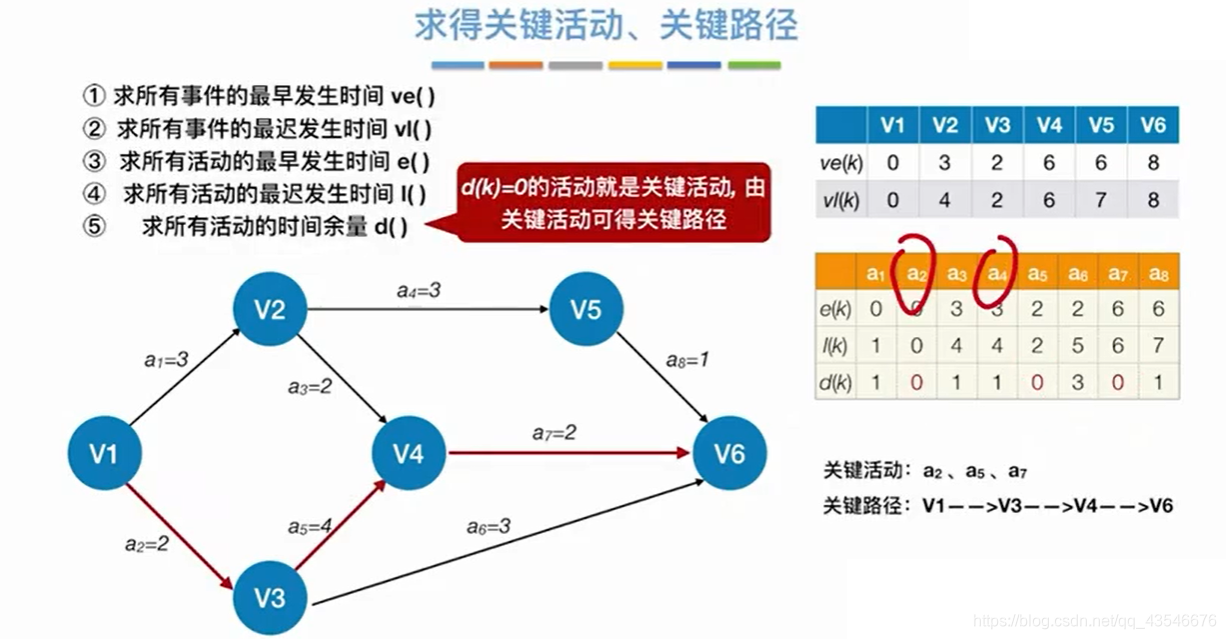
8.3 关键路径特性
1. 若关键活动的时间增加,则整个工程的工期将增加。
2. 一定范围内缩短关键活动的时间,可以缩短整个工程的工期;缩短到一定程度,关键活动可能变为非关键活动。
3. 可能有多条关键路径,只提高一条路径上的关键活动速度并不能缩短整个工程的工期,只用加快所有关键路径的才可以。
8.4 小结
9. 一些小知识点
1. 能判断图是否有环的方法:
1. DFS
2. 拓扑或逆拓扑排序
3. 关键路径(这个比较模糊,可以判断环也可以不判断环,看题目情况,但是上面两个是必定可以判断是否有环)
* 注意:BFS和最短路径不能判断是否有环,所以求关键路径的第一步——要进行拓扑排序。
2. 有向无环图的DFS序列是拓扑排序,若是DFS算法退栈返回时打印相应的顶点,则输出的是逆拓扑排序。
3. 深度优先搜索生成树的高度 >= 广度优先搜索生成树的高度
原因:BFS可用于单源最短路径,所以得到的树会尽可能的矮;深度优先搜索会尽可能深的搜索树,路径会尽可能的长。
4. 只要无向连通图中没有权值相等的边,则最小生成树唯一;而有相等的边时,可能唯一,也可能不唯一,比如当其本身是一棵树时,其最小生成树唯一。
5. 连通图的最小生成树的可能不唯一,但是其代价一定唯一。(代价指的是所有边的权值之和)
6. 连通图的权值最小的边不一定出现在最小生成树中,如果该边在环中,则可能不会出现在最小生成树中。
7. 对于遍历图的操作,比如DFS,BFS,拓扑排序等算法复杂度都与图本身的存储结构有关。
8. 如果不能进行拓扑排序,则有向图一定存在回路。其等价说法是:
* 顶点数目大于1的强连通分量中必然存在回路,因为两个顶点的强连通图就以及形成了环。
* 注意:这种说法是错误的:该图是强连通图。 因为可能是非连通有向图
9. 拓扑排序中暂存度为0的结点可以用栈也可以用队列。
10. 一个有向图具有有序的拓扑排序,则它的邻接矩阵为三角。
一个有向图具有拓扑排序,则它的邻接矩阵为一般。
* 注意:区别在于其拓扑排序是否有序。
11. 有向无环图有唯一拓扑序列并不能唯一确定该图。
12. 关键活动一定位于关键路径上
13. 若有向图的邻接矩阵中对角线以上的元素全为1,以下的全为,则其拓扑排序存在且唯一。
若有向图的邻接矩阵中对角线以下的全为,则其拓扑排序存在,但是可能唯一。