张量基础学习 （三 张量代数运算———上）

经过前面几期博客的学习，我们初步认识了张量的基本概念，一些重要的符号与指标，坐标的变换规律和相应的张量的分量转化规律之后，接下里，将持续学习张量的各种运算法则与规律！

本人励志做最详细的博客撰写，所以加入许多基础性的知识，既为小白的理解铺垫，也为大神的日后一鸣惊人复习奠基！所以有时候前期会有较大篇幅的铺垫只为后面的一个小知识点，还请大家莫怪！

一 . 佛系张量代数

下面我们会一股脑的学习一大堆概念与运算法则，大家加油顶住！张量有很多个维度，层次的，为了新手入门理解，我们这里全部用一阶张量或者二阶张量代替高阶的！

（1）和差，数乘，相等关系

毫无疑问张量也满足一些最基本代数运算，我们在这里就一带而过了。

1) 若两个张量相等，即 $\boldsymbol{T} = T_{ij}e_{i}e_{j}$ 和 $\boldsymbol{S} = S_{ij}e_{i}e_{j}$ 相等，那么他们对应的分量 也满足 $T_{ij} = S_{ij}$
2) 两个张量相加减也就是其对应的分量相加减：新得到的张量为: $Z_{ij} =T_{ij}\pm S_{ij}$
3) 某个张量 $\boldsymbol{A}$ 和 一个数 $\lambda$ 相乘之后，得到新张量的维度没有变化，且分量也进行的同样的数乘运算。
4) 高中我们就学过向量的数量级运算（这里就提一下，不多做介绍），我们一般认为它是矢量之间的“点乘” ,后来 在高数中学到了“叉乘” ，马上就会介绍！

（2）Polar and Axial Vectors

张量学习的最终目的是为物理，数学的现实科研贮备，我们先来带大家回顾一下 极轴矢量 这个老盆友，学物理的盆友们应该很熟悉，无奈我是程序员，没学过啊~~

三维欧几里得空间中的向量被定义为具有特定标量值大小和方向的有向线段。向量a的大小(长度)用 $|a|$表示。两个向量a和b是相等的，如果它们有相同的方向和大小。向量 $\boldsymbol{0}$ 的大小等于0。在力学中可以引入两种类型的向量:

1. 第一类向量是有向线段。这些向量与三维空间中的平动有关。物理上的例子包括力，位移，速度，加速度，动量。
2. 第二类用于描述旋量运动及其相关量，即旋量、力矩、角速度、角动量等，下图中显示了所谓的自旋向量a∗，它表示绕给定轴的旋转。旋转的方向由圆形箭头指定，旋转的“幅度”是对应的长度！
   

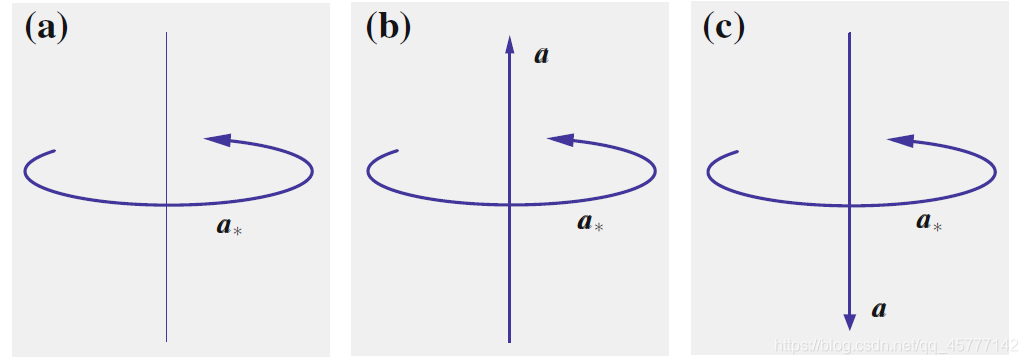
这其实就是我们高中物理学的各种电磁规律，右手定则等等似乎都用到了这样的图！有下面三个注意点：

• 向量 $\boldsymbol{a}$ 位于在自旋向量的轴上。
• 向量 $\boldsymbol{a}$的大小等于 $\boldsymbol{a_{*}}$的大小 。
• 分别满足左手定则与右手定则！（这个相信大家一样就看出来了!!!∑(ﾟДﾟノ)ノ）。

（3）Vector (Cross) Product of Two Vectors

$\boldsymbol{c} = \boldsymbol{a}\times \boldsymbol{b}$ 分三步理解：

1. 这个轴正交于在 $\boldsymbol{a}$ s和 $\boldsymbol{b}$上张成的平面。如图（a）
   
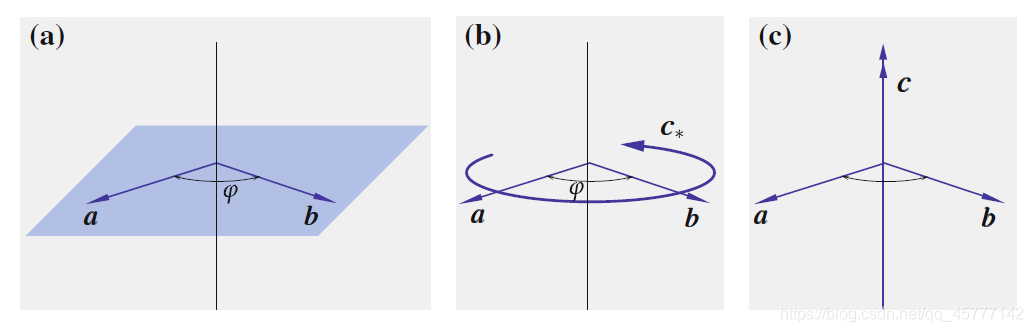
2. 圆形箭头表示从 $\boldsymbol{a}$到 $\boldsymbol{b}$ 的 “最短” 旋转方向！如图（b）
3. $\boldsymbol{c_{*}}$的长度为： $\left |a\right | \left |b\right | sin \varphi$ ，其中 $\varphi$ 从 $\boldsymbol{a}$到 $\boldsymbol{b}$ 的 “最短” 旋转方向夹角！

我们都知道张量有内积，这里的我们把这个“叉乘” 又叫做外积，注意：从数学意义上来说，外积只有向量才有，不是所有的张量都有，说=到这里，你是否能依稀回忆起我们在遥远的美好的青涩的大一时用内积来求空间几何的平面法向量！

我们在前面学到的能量本征方程和后面将要学到的 量子力学中的 本征值与分离能级 也需要用到这里的知识！下面简单看一看它的运算法则：

$\begin{array}{l}a \times b=-b \times a \\a \times(b+c)=a \times b+a \times c\end{array}$

外积和内积也可以结合起来，称为混合积 ，用 $\boldsymbol{a}，\boldsymbol{b}，\boldsymbol{c}$ 表示混合积是 $(\boldsymbol{b}\times \boldsymbol{a}) \cdot \boldsymbol{c}$，它的结果是一个标量，并且有恒等式如下：
$\boldsymbol{a} \cdot(\boldsymbol{b} \times \boldsymbol{c})=\boldsymbol{b} \cdot(\boldsymbol{c} \times \boldsymbol{a})=\boldsymbol{c} \cdot(\boldsymbol{a} \times \boldsymbol{b})$
连续两次外积运算可以转化为点乘形式：
$\boldsymbol{a}\times(\boldsymbol{b}\times\boldsymbol{c}) =\boldsymbol{b}(\boldsymbol{a}\cdot\boldsymbol{c})- \boldsymbol{c}(\boldsymbol{a}\times\boldsymbol{b})$
进一步，联立上述紫色的二式可以得到：
$\begin{aligned} (\boldsymbol{a} \times \boldsymbol{b}) \cdot(\boldsymbol{c} \times \boldsymbol{d}) &=\boldsymbol{a} \cdot[\boldsymbol{b} \times(\boldsymbol{c} \times \boldsymbol{d})] \\ &=\boldsymbol{a} \cdot(\boldsymbol{c} \boldsymbol{b} \cdot \boldsymbol{d}-\boldsymbol{d} \boldsymbol{b} \cdot \boldsymbol{c}) \\ &=\boldsymbol{a} \cdot \boldsymbol{c} \boldsymbol{b} \cdot \boldsymbol{d}-\boldsymbol{a} \cdot \boldsymbol{d} \boldsymbol{b} \cdot \boldsymbol{c} \end{aligned}$

二. 几个 “积” ！

（1）并积（总）

两个张量 $\boldsymbol{A}$ 和 $\boldsymbol{B}$ 并积得到的 $\boldsymbol{A}$是一个阶数等于A 与B 阶数之和的高阶张量！

设 $\boldsymbol{A} =A_{ijk}e_{i}e_{j}e_{k}$ ， $\boldsymbol{B} =B_{lm}e_{l}e_{m}$. 则幷积得到的新张量为：
$\boldsymbol{T}=\boldsymbol{A} \boldsymbol{B}=T_{i j k l m} \boldsymbol{e}_{i} \boldsymbol{e}_{j} \boldsymbol{e}_{k} \boldsymbol{e}_{l} \boldsymbol{e}_{m}$

我举个小例子可能会帮助大家理解：
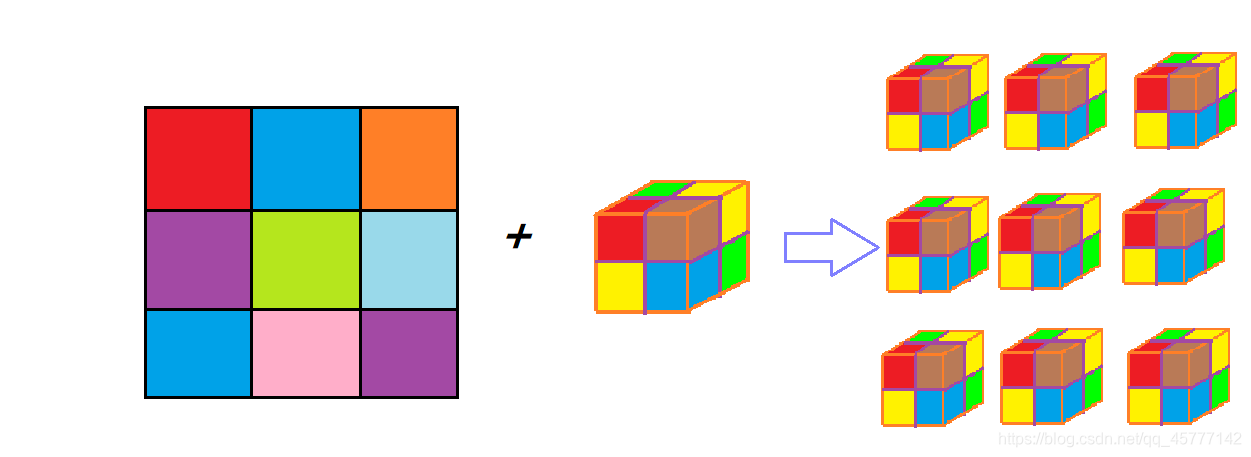定义中使用二阶张量与三阶张量相加，这个我们用平面的9方格代替二维张量，用二阶魔方代替三维张量，将魔方依次放到九方格中形成的如上图形就是五维张量，大概的意思就是这样！

并积还有几种特殊的情况，我们接下来再看看！

（2） $Kronecker$ $product$

$Kronecker$ 积在张量计算中非常常见，是衔接矩阵计算和张量计算的桥梁，实际上，Kronecker积的运算规则是很简单的，给定一个大小为 $n_{1}\times n_{2}$的矩阵 $\boldsymbol{B}$ 和一个大小为 $m_{1}\times m_{2}$的矩阵 $\boldsymbol{A}$，则矩阵 $\boldsymbol{A}$ 和矩阵 $\boldsymbol{B}$ 的Kronecker积为:
$A \otimes B=\left[\begin{array}{cccc} a_{11} B & a_{12} B & \cdots & a_{1 m_{2}} B \\ a_{21} B & a_{22} B & \cdots & a_{2 m_{2}} B \\ \vdots & \vdots & \ddots & \vdots \\ a_{m_{1} 1} B & a_{m_{1} 2} B & \cdots & a_{m_{1} m_{2}} B \end{array}\right]$

很明显，矩阵 $A \otimes B$ 的大小为 $(m_{1}n_{1}) \times(m_{2}n_{2})$，即行数为 $m_{1}n_{1}$，列数为 $m_{2}n_{2}$

其实您完全可以这么理解， $\boldsymbol{A}$ 不动，每个元素乘以矩阵 $\boldsymbol{B}$，之后就是逐个代入计算，做个题目压压惊：

给定 $A=\left[\begin{array}{ll}1 & 2 \\ 3 & 4\end{array}\right], \quad B=\left[\begin{array}{lll}5 & 6 & 7 \\ 8 & 9 & 10\end{array}\right]$，则：

$A \otimes B=\left[\begin{array}{lll} 1 \times\left[\begin{array}{lll} 5 & 6 & 7 \\ 8 & 9 & 10 \end{array}\right] & 2 \times\left[\begin{array}{lll} 5 & 6 & 7 \\ 8 & 9 & 10 \end{array}\right] \\ 3 \times\left[\begin{array}{lll} 5 & 6 & 7 \\ 8 & 9 & 10 \end{array}\right] & 4 \times\left[\begin{array}{lll} 5 & 6 & 7 \\ 8 & 9 & 10 \end{array}\right] \end{array}\right]$
即：
$A \otimes B=\left[\begin{array}{cccccc} 5 & 6 & 7 & 10 & 12 & 14 \\ 8 & 9 & 10 & 16 & 18 & 20 \\ 15 & 18 & 21 & 20 & 24 & 28 \\ 24 & 27 & 30 & 32 & 36 & 40 \end{array}\right]$

注意：次矩阵乘法规律不满足乘法交换律哦 ！ 也就是： $A \otimes B\neq B \otimes A$ ，，这里也补充其相关数学运算性质：
$\begin{aligned} \mathbf{A} \otimes(\mathbf{B}+\mathbf{C}) &=\mathbf{A} \otimes \mathbf{B}+\mathbf{A} \otimes \mathbf{C} \\ (\mathbf{B}+\mathbf{C}) \otimes \mathbf{A} &=\mathbf{B} \otimes \mathbf{A}+\mathbf{C} \otimes \mathbf{A} \\ (k \mathbf{A}) \otimes \mathbf{B} &=\mathbf{A} \otimes(k \mathbf{B})=k(\mathbf{A} \otimes \mathbf{B}) \\ (\mathbf{A} \otimes \mathbf{B}) \otimes \mathbf{C} &=\mathbf{A} \otimes(\mathbf{B} \otimes \mathbf{C}) \\ \mathbf{A} \otimes \mathbf{0} &=\mathbf{0} \otimes \mathbf{A}=\mathbf{0} \end{aligned}$

（3） $Hadamard$ $product$

Hadamard 乘积定义在两个大小相同的矩阵 $\mathbf{A} \in \mathbb{R}^{I \times J}, \mathbf{B} \in \mathbb{R}^{I \times J}$ 上，运算法则如下如下：
$\mathbf{A} * \mathbf{B}=\left[\begin{array}{cccc} a_{11} b_{11} & a_{12} b_{12} & \cdots & a_{1 J} b_{1 J} \\ a_{21} b_{21} & a_{22} b_{22} & \cdots & a_{2 J} b_{2 J} \\ \vdots & \vdots & \ddots & \vdots \\ a_{I 1} b_{I 1} & a_{I 2} b_{I 2} & \cdots & a_{I J} b_{I J} \end{array}\right] \in \mathbb{R}^{I \times J}$

有一个细节需要注意：这个的运算符号 $\circ$ 与后面使用的 $*$ 是一样的，我们平时用的更多的是： $*$.
易知，新生成矩阵的行列数都没有发生变化，里面的元素也是对应相乘，举个例子：
$\left[\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right]* \left[\begin{array}{lll} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33} \end{array}\right]=\left[\begin{array}{lll} a_{11} b_{11} & a_{12} b_{12} & a_{13} b_{13} \\ a_{21} b_{21} & a_{22} b_{22} & a_{23} b_{23} \\ a_{31} b_{31} & a_{32} b_{32} & a_{33} b_{33} \end{array}\right]$
这里顺便介绍一下基本性质：
$\begin{array}{l} \mathbf{A} * \mathbf{B}=\mathbf{B} * \mathbf{A} \\ \mathbf{A}* (\mathbf{B} * \mathbf{C})=(\mathbf{A} * \mathbf{B}) * \mathbf{C} \\ \mathbf{A} *(\mathbf{B}+\mathbf{C})=\mathbf{A} * \mathbf{B}+\mathbf{A} * \mathbf{C} \\ (k \mathbf{A}) * \mathbf{B}=\mathbf{A} *(k \mathbf{B})=k(\mathbf{A} * \mathbf{B}) \\ \mathbf{A} * \mathbf{0}=\mathbf{0} * \mathbf{A}=\mathbf{0} \end{array}$

（4） $Khatri-Rao$ $product$

给定大小为 $I\times k$ 的矩阵 $A=\left(\vec{a}_{1}, \vec{a}_{2}, \ldots, \vec{}_{k}\right)$和大小为 $J\times k$， $B=\left(\vec{b}_{1}, \vec{b}_{2}, \ldots, \vec{b}_{k}\right)$,，则矩阵 $\boldsymbol{A}$ 和 $\boldsymbol{B}$ 的Khatri-Rao 积为：
$A \odot B=\left(\vec{a}_{1} \otimes \vec{b}_{1}, \vec{a}_{2} \otimes \vec{b}_{2}, \ldots, \vec{a}_{k} \otimes \vec{b}_{k}\right)$
也阔以看图~~
还是来做个题目帮助理解：

给定矩阵： $A=\left[\begin{array}{ll}1 & 2 \\ 3 & 4\end{array}\right]=\left(\vec{a}_{1}, \vec{a}_{2}\right), \quad B=\left[\begin{array}{cc}5 & 6 \\ 7 & 8 \\ 9 & 10\end{array}\right]=\left(\vec{b}_{1}, \vec{b}_{2}\right)$
则：
$A \odot B=\left(\vec{a}_{1} \otimes \vec{b}_{1}, \vec{a}_{2} \otimes \vec{b}_{2}\right)=\left[\left[\begin{array}{l} 1 \\ 3 \end{array}\right] \otimes\left[\begin{array}{l} 5 \\ 7 \\ 9 \end{array}\right] \quad\left[\begin{array}{l} 2 \\ 4 \end{array}\right] \otimes\left[\begin{array}{c} 6 \\ 8 \\ 10 \end{array}\right]\right]$

最终结果为： $A \odot B=\left[\begin{array}{cc}5 & 12 \\ 7 & 16 \\ 9 & 20 \\ 15 & 24 \\ 21 & 32 \\ 27 & 40\end{array}\right]$ ，还需要注意这里的积运算也是不满足交换律的！

大家一定要好好比较这三种 “积” 区别与联系！为大家整理好：