题目大意:
给定一棵带边权和点权的无根树\(T\),求找到一个点\(x\)使\(\sum_{u\in T} dis_{x,u}\times c_u\)取得最小。
对于所有数据,有\(1≤N≤10^5,1≤c_i≤10^3\)
考虑手玩样例找规律(默认以1为根,当然也可以以其他点为根)
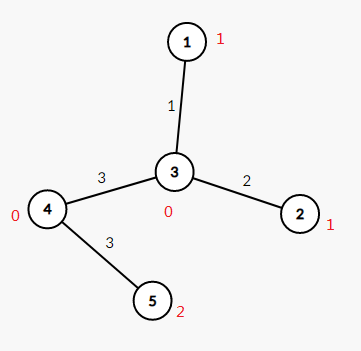
假设我们有\(f[i]\)表示选择节点\(i\)的最小不方便度。
那么\(f[1]=2\times 7+1\times 3=17\)。如果用暴力来求得每一个\(f[i]\),那么时间复杂度达到\(O(n^2)\),铁定炸。
于是就要考虑充分利用已知的数据。
已知\(f[1]\),要求得\(f[3]\),有没有什么快速的办法?
在已经到达1的奶牛中,有一部分是从(3的子树)中经过(1,3)完成的,另一部分是从(3的子树以外的节点)到达1的。在这个图中,因为3是根节点的唯一儿子,所以另一部分不存在。
所以要让所有奶牛都到达3,就分以上两类讨论。
(3的子树中的点)因为多走了(1,3)这条边,所以退回来只需要在它们原有到1的基础花费(记为a)上减去(3的子树中的点)乘上(1,3)的权值。
(3的子树外的点)因为少走了(1,3)这条边,所以往前走只需要在它们原有到1的基础花费(记为b)上加上(3的子树外的点)乘上(1,3)的权值。
我们发现,a,b两部分相加,其实就是\(f[1]\)。
(3的子树内的点)本质是统计一棵子树的点权和,可以通过一次dfs完成,记为\(sz[3]\)。
(3的本质外的点)只需要把所有点权加起来(\(sum\)),再减去\(sz[3]\)即可。
回到题目。
我们只需要\(O(n)\)把任意一个点作为根节点,求出它的\(f[i]\),然后进行第二次dfs按照上面的规则,\(O(1)\)就可以从父节点转移到子节点。
\(f[v]=f[u]-sz[v]*w+(sum-sz[v])*w\)
所以...最终的时间复杂度是\(O(n)\)级别的。
注意开\(longlong\),否则\(N*C_i*L_i\)会超过\(int\)。
#include<bits/stdc++.h>
#define int long long
#define INF 1e15
using namespace std;
const int N=1e5+10;
int head[N<<1],to[N<<1],nxt[N<<1],val[N<<1],cnt,n;
int c[N];
void add(int u,int v,int w)
{
cnt++;
to[cnt]=v;
val[cnt]=w;
nxt[cnt]=head[u];
head[u]=cnt;
}
int sz[N],d[N],sum;
void dfs1(int u,int fa)
{
sz[u]+=c[u];
for(int i=head[u];i;i=nxt[i])
{
int v=to[i],w=val[i];
if(v==fa)continue;
d[v]=d[u]+w;
dfs1(v,u);
sz[u]+=sz[v];
}
return;
}
int f[N];
void dfs2(int u,int fa)
{
for(int i=head[u];i;i=nxt[i])
{
int v=to[i],w=val[i];
if(v==fa)continue;
f[v]=f[u]+(sum-2*sz[v])*w;
dfs2(v,u);
}
}
signed main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
scanf("%lld",&c[i]);
sum+=c[i];
}
for(int i=1;i<n;i++)
{
int x,y,z;
scanf("%lld%lld%lld",&x,&y,&z);
add(x,y,z);
add(y,x,z);
}
dfs1(1,0);
for(int i=2;i<=n;i++)
f[1]+=(d[i]*c[i]);
dfs2(1,0);
int ans=INF;
for(int i=1;i<=n;i++)
ans=min(ans,f[i]);
printf("%lld\n",ans);
return 0;
}