「Wallace 笔记」快速上手回文自动机（PAM）

Content

简述
概念
结构
构建
实现
正确性
后记

简述

回文树（EER Tree）是可以存储一个字符串的 所有回文字串 的一种实用数据结构。

回文自动机（PAM）是存储了这个字符串的所有回文串信息的自动机。

事实上这两个是一个东西，是一个高效处理回文相关问题的利器 。

概念

回文自动机是一类可以接受字符串的所有回文子串的自动机。

结构

1.结构特点

我们知道回文串大多分奇偶讨论

有一种被称为 manacher 的算法，被广泛用于解决回文问题。它是通过在字符间插入不属于字符集的分隔符（如 # 或 $ 等）处理的。

但 PAM 一般不这么干——我们一般 直接按奇偶分为两个部分。

那么就会有两个根节点：奇根和偶根。

OI-wiki 上的演示图片：

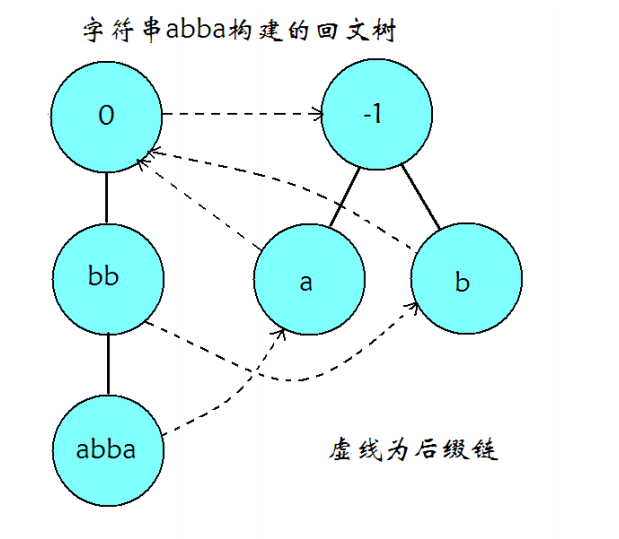
2. 状态

既然可以被称为“自动机”，那么一定有状态。

PAM 的一个状态表示 原串的一个回文字串。

状态中除了转移函数的值，还存储了最基础的两个字段：fail 和 len。分别表示 后缀链接，以及 当前状态的结点所代表的最长回文字串的长。

后缀链接具体见下文。

奇根和偶根并不代表任何串，仅作为初始状态存在。

特别的，我们令奇根的 $\text{len} = -1$，偶根的 $\text{len} = 0$。

所有的状态都代表一个本质不同的回文子串，PAM 中又存储了所有回文子串的信息，那么 PAM 的状态数减一（除去奇根）等于原串本质不同的回文子串个数。

3. 转移

PAM 的转移函数比较特殊。

如果结点 $x$ 走了一条字符 $c$ 的转移，那么表示在 $x$ 的 当前回文子串前后各加一个字符 $c$ 。

这个并不难理解——因为必须满足回文性质。

4. `fail` 指针

即后缀链接。

对于一个状态 $x$，其 $\text{fail}$ 指针所指的状态 $y$，代表的最长回文串满足，后者为前者的最长回文真后缀。

特别的，偶根的 $\text{fail} = $ 奇根，至于奇根的 $\text{fail}$ 我们不需要管，因为长度为 1 的字串必定为回文串，不可能失配。

建出 PAM 后，fail 指针将结点连成了一颗树形结构—— fail 树。

构建

和 SAM 一样，我们用 增量法 构造 PAM，即在线算法。

我们假设对 $S$ 构造 PAM，当前位置为 $p$。现在将 $S_p$ 插入 PAM。

首先找到上一次插入 $S_{p - 1}$ 的结点 $x$，判断是否满足 $S_{p} = S_{p - \text{len}(x) - 1}$，即待添加的字符与当前回文子串 的前一个字符 是否相同。

若相同那么直接找转移边，否则就需要跳 fail 指针。一直跳，直至条件 $S_{p} = S_{p - \text{len}(x) - 1}$ 被满足。（跳到最后可能会跳到根，但此时条件成了 $S_{p} = S_{p}$，而这显然成立不可能继续回跳，因此不需要过于在意边界处理）

于是现在我们将 $x$ 跳转到了正确的位置，可以进行插入了！

如果发现转移 $S_p$ 字符的转移已存在，那么就基本完成了，反之则需新建结点（以下称 $y$）。

上文提到 PAM 的结点中至少维护两个字段——len 和 fail。

前者不难得到，回顾转移的定义，是在首位两端加入字符，于是有 $\text{len}(y) = \text{len}(x) + 2$。

但如何求 $\text{fail}$？我们从 $\text{fail}(x)$ 开始跳 $\text{fail}$ 指针，从 $x$ 代表的最长回文后缀起步，直至满足前后匹配然后取转移即可。顺带一提，这里的跳 $\text{fail}$ 与上面的其实非常相似。

如果没得匹配，和上面一样会得到 $\text{fail}(y) = 0$ 的结果，不过不会有任何不妥——空串为任何串的后缀。

以上，我们完成了一个字符的插入。

附上图示：

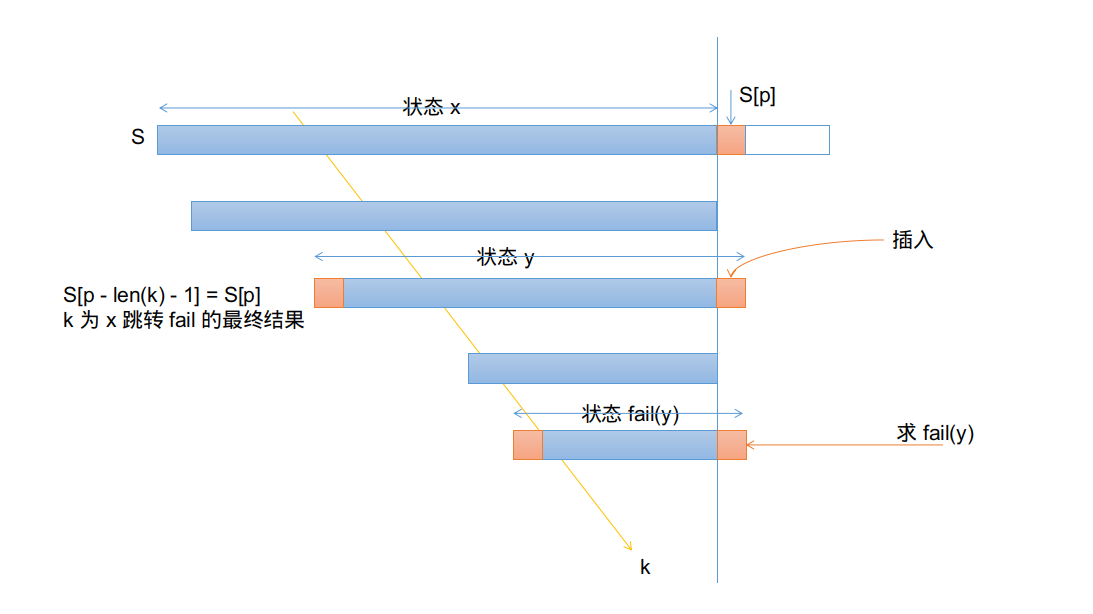
实现

1. 基础设置

struct Node { // 结点（状态）结构体
    int ch[S], fail; // 转移，失配指针
    int len; // 当前状态可以表示的最长回文子串的长
} t[N];
int total, last;
// 总点数，上一次更新的点的标号
void init() { // 初始化
    t[0].fail = 1, t[1].fail = 0;
    t[0].len = 0, t[1].len = -1;
    total = 1, last = 0;
}
int create(int l) { // 创建 len = l 的新结点
    int x = ++total;
    t[x].len = l, t[x].fail = 0;
    return x;
}

2. 跳转 `fail` 函数

// 跳转 fail : 从结点 x 起，跳转以配对 s[p]
int getFail(int x, int p) {
    while (s[p] != s[p - t[x].len - 1])
        x = t[x].fail; // 不匹配则一直跳
    return x;
}

3. 构造算法主体 `extend`

// 增量构造 : 添加字符 s[p]（主串为 s[1, n]）
void extend(int p) {
    int x = getFail(last, p); // 从上一次添加的位置起，跳 fail 到可添加的位置
    if (t[x].ch[s[p] - 'a'] == 0) { // 跳完了，如果没有转移，那么新建
        int y = create(t[x].len + 2); // 新建结点 y : 注意 len 是前面与后面各一个字符，因此 +2
        t[y].fail = t[getFail(t[x].fail, p)].ch[s[p] - 'a']; // 得到 y 的 fail 指针，取转移
        t[x].ch[s[p] - 'a'] = y; // y 为 x 的某一个转移的值，更新转移函数值
    }
    last = t[x].ch[s[p] - 'a']; // 更新 last
}

正确性

进行了我们将对 PAM 的构建算法进行正确性（复杂度）证明。

命题 1. 一个字符串 $S$ 的本质不同的回文子串个数不超过 $|S|$ 个。

证明： 数学归纳法。（部分参考自 OI-wiki）

$|S| = 1$ 时，显然。
$|S| \ge 2$ 时，假设 $S$ 尾部加上某一个字符 $c$ 为 $T$，并且 $S$ 满足此命题。
- 我们设 $T$ 的所有回文真后缀为 $T[l_1, |T|], T[l_2, |T|], \cdots , T[l_k, |T|]$，其中 $l_i < l_{i + 1}$。因为 $T[l_1, |T|]$ 是回文串，于是所有 $\in [l_1, |T|]$ 的位置 $p$ 满足 $T[p, |T|] = T[l_1, l_1 + |T| - p]$。
- 那么对于任意一个 $i \in (1, k]$，由于 $T[l_i, |T|]$ 是 $T[l_1, |T|]$ 的一个子串，于是 $T[l_i, |T|]$ 的反串 一定在 $T[1, |T| - 1]$ 中出现过。然而 $T[l_i, |T|]$ 也是回文的，正串就是反串，所以得出结论：只有 $T[l_1, |T|]$ 可能被作为新的本质不同的回文子串。
- 一个字符最多新增一个本质不同的回文子串，所以该命题得证。

命题 2. PAM 上的状态数为 $O(|S|)$。

证明： 因为 PAM 上的状态数等于本质不同的回文子串个数，结合命题 1 即可得证。

或者说，由 PAM 构造算法，可得一次 extend 至多增加一个结点。那么 $|S|$ 次添加显然有 $O(|S|)$ 个结点。

命题 3. PAM 构造算法的时间复杂度为 $O(|S|)$。

证明： 观察上述构造算法，发现仅有 getFail 函数的复杂度难以证明。跳 fail 指针，连 fail 可以视作在 fail 树上跳祖先，建边。

在 fail 树上，每次跳 fail 时深度 $-1$，每次建 fail 边时深度 $+1$。

而在建 fail 指针时，我们发现是从 $\text{fail}(x)$ 开始跳的，因此深度 $-1$，而最终深度只会 $+1$。于是整棵 fail 树深度 $\le |S|$。

那么易知跳的次数不超过 $O(|S|)$，于是构建算法的时间复杂度也为 $O(|S|)$。

后记

原文地址：https://www.cnblogs.com/-Wallace-/p/13375265.html
本文作者：@-Wallace-
转载请附上出处。