函数图像上存在对称点

前言

从数的角度来说，

若函数$f(x)$与函数$g(x)$的图像上存在关于$x$轴的对称点，则$f(x)=-g(x)$有解；

若函数$f(x)$与函数$g(x)$的图像上存在关于$y$轴的对称点，则$f(-x)=g(x)$有解；

若函数$f(x)$与函数$g(x)$的图像上存在关于原点的对称点，则$f(x)=-g(-x)$有解；

从形的角度来说，

若函数$f(x)$与函数$g(x)$的图像上存在关于$x$轴的对称点，则函数$y=f(x)$与函数$y=-g(x)$的图像有交点；

若函数$f(x)$与函数$g(x)$的图像上存在关于$y$轴的对称点，则函数$y=f(-x)$与函数$y=g(x)$的图像有交点；

若函数$f(x)$与函数$g(x)$的图像上存在关于原点的对称点，则函数$y=f(x)$与函数$y=-g(-x)$的图像有交点；

分类解析

两个函数图像上存在关于$x$轴的对称点类问题

例1 【2017•蚌埠模拟】已知函数$f(x)=lnx-x^3$与$g(x)=x^3-ax$的图像上存在关于$x$轴的对称点，则$a$的取值范围为【】

$A.(-\infty，e)$ $B.(-\infty，e]$ $C.(-\infty，\cfrac{1}{e})$ $D.(-\infty，\cfrac{1}{e}]$

法1分析：函数$f(x)=lnx-x^3$与$g(x)=x^3-ax$的图像上存在关于x轴的对称点，

即当$x=x_0$时，$f(x_0)=-g(x_0)$。

所以方程$f(x)=-g(x)$有解，所以$lnx-x^3=-x^3+ax$有解，

所以$lnx=ax$在$(0,+\infty)$有解，即方程$a=\cfrac{lnx}{x}$在$(0,+\infty)$有解，

令$h(x)=\cfrac{lnx}{x}$，由导数知识可知，$f(x)$在$(0，e)$上单调递增，在$(e，+\infty)$上单调递减，

又$f(e)=\cfrac{1}{e}$，故函数$h(x)\in (-\infty，\cfrac{1}{e}]$，故$a$的取值范围为$(-\infty，\cfrac{1}{e}]$ ，选$D$。

法2：转换为方程$lnx=ax$在$(0,+\infty)$有解，即函数$y=lnx$和函数$y=ax$图像在$(0,+\infty)$上有交点，利用数形结合求解；

法3：接上转换为方程$a=\cfrac{lnx}{x}$在$(0,+\infty)$有解，即函数$y=h(x)=\cfrac{lnx}{x}$和函数$y=a$的图像有交点，利用数形结合求解；

两个函数图像上存在关于$y$轴的对称点类问题

例2 【2018陕西省高三第二次质检第12题】已知函数$f(x)=e^x+2(x<0)$与$g(x)=ln(x+a)+2$的图像上存在关于$y$轴对称的点，则则$a$的取值范围为【】

$A.(-\infty，\cfrac{1}{e})$ $B.(-\infty，e)$ $C.(-\cfrac{1}{e}，e)$ $D.(-e，\cfrac{1}{e}]$

分析：函数$f(x)=e^x+2(x<0)$与$g(x)=ln(x+a)+2$的图像上存在关于$y$轴对称的点，即$f(-x_0)=g(x_0)$能成立。

即方程$f(-x)=g(x)$有解，所以当$x>0$时，$e^{-x}+2=ln(x+a)+2$有解，

即方程$e^{-x}=ln(x+a)$在$x>0$时有解，即函数$y=e^x$与函数$y=ln(x+a)$图像有交点，

法1：数形结合法，如右图所示可知，当函数$y=ln(x+a)$过点$(1，0)$时，没有交点，

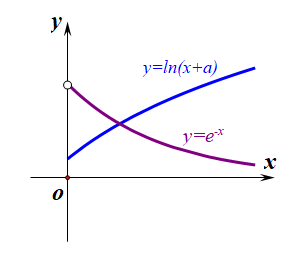
此时由$ln(0+a)=1$可得，$a=e$；

又由图像平移可知，需要将函数$y=ln(x+a)$向右移动才会有交点，

故$a<e$，即$a$的取值范围是$(-\infty，e)$，选$B$.

法2：补集思想+计算法，由图可知，当函数$y=ln(x+a)$经过点$(0，1)$上方时，必无交点，

即$lna\ge 1$时，即$a\ge e$时，二者无交点，由补集思想可得，二者有交点时$a<e$，

即$a$的取值范围是$(-\infty，e)$，选$B$.

解后反思：在网上见到有人这样解，$lna<1$，解得$0<a<e$，这是错的(很显然，$a=0$是满足的)，原因是当$a<0$时，$lna$是没有意义的，但是此时函数$y=ln(x+a)$的图像已经和$y$轴没有交点了，已经向右移动了，其渐近线也是向右移动的。

练1 【学生训练题目】已知函数$f(x)=x^2+e^x-\cfrac{1}{2}(x<0)$与函数$g(x)=x^2+\ln(x+a)$的图像上存在关于$y$轴的对称点，则$a$的取值范围是【】

$A.(-\infty，\sqrt{e})$ $B.(-\sqrt{e}，\cfrac{\sqrt{e}}{e})$ $C.(-\infty，\cfrac{\sqrt{e}}{e})$ $D.(-\cfrac{\sqrt{e}}{e}，\sqrt{e})$

提示：答案为$A$，请仿上例完成。

两个函数图像上存在关于原点的对称点类问题

例3 【学生训练题目】已知函数$f(x)=lnx-x^2$与函数$g(x)=x^2-\cfrac{2}{x}-m$的图像上存在关于原点的对称点，则$m$的取值范围为________.

分析：由题可知，方程$f(x)=-g(-x)$在$x>0$上有解，即$lnx-x^2=-x^2-\cfrac{2}{x}+m$在$x>0$上有解，

则$m=lnx+\cfrac{2}{x}$在$x>0$上有解，设$h(x)=lnx+\cfrac{2}{x}(x>0)$，

则$h'(x)=\cfrac{1}{x}-\cfrac{2}{x^2}=\cfrac{x-2}{x^2}$，

故$h(x)$在区间$(0，2)$上单调递减，在区间$(2，+\infty)$上单调递增，

则$h(x)_{min}=h(2)=ln2+1$

即函数$h(x)$的值域是$[ln2+1，+\infty)$

故$m$的取值范围为是$[ln2+1，+\infty)$。

例4 【学生训练题目】已知函数$f(x)=\left\{\begin{array}{l}{\cos(\cfrac{\pi}{2}x)-1，x\leqslant 0}\\{-log_a(-x)，x<0}\end{array}\right.(a>0，a\neq 1)$，若函数图像上关于原点对称的点至少有$3$对，则实数$a$的取值范围是【】

$A.(0，\cfrac{\sqrt{6}}{6})$ $B.(\cfrac{\sqrt{6}}{6}，1)$ $C.(0，\cfrac{\sqrt{5}}{5})$ $D.(\cfrac{\sqrt{5}}{5}，1)$

提示：选$A$，有时间整理；

函数图像上存在对称点

前言

分类解析

猜你喜欢