首先,什么是凸包?
假设平面上有p0~p12共13个点,过某些点作一个多边形,使这个多边形能把所有点都“包”起来。当这个多边形是凸多边形的时候,我们就叫它“凸包”。
处理何种问题:凸包可以看成在木板上钉许多钉子,用一根橡皮筋框住所有钉子所得到的多边形,最终能求得都由哪些钉子构成该凸包。如下图所示:

然后,什么是凸包问题?
我们把这些点放在二维坐标系里面,那么每个点都能用 (x,y) 来表示。
现给出点的数目13,和各个点的坐标。求构成凸包的点?
解一:穷举法(蛮力法)
时间复杂度:O(n³)。
思路:两点确定一条直线,如果剩余的其它点都在这条直线的同一侧,则这两个点是凸包上的点,否则就不是。
步骤:
将点集里面的所有点两两配对,组成 n(n-1)/2 条直线。
对于每条直线,再检查剩余的 (n-2) 个点是否在直线的同一侧。
如何判断一个点 p3 是在直线 p1p2 的左边还是右边呢?(坐标:p1(x1,y1),p2(x2,y2),p3(x3,y3))
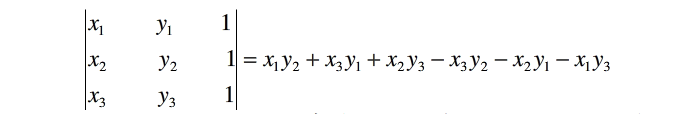
当上式结果为正时,p3在直线 p1p2 的左侧;当结果为负时,p3在直线 p1p2 的右边。
解二:分治法
时间复杂度:O(n㏒n)。
思路:应用分治法思想,把一个大问题分成几个结构相同的子问题,把子问题再分成几个更小的子问题……。然后我们就能用递归的方法,分别求这些子问题的解。最后把每个子问题的解“组装”成原来大问题的解。
步骤:
1.把所有的点都放在二维坐标系里面。那么横坐标最小和最大的两个点 P1 和 Pn 一定是凸包上的点(为什么呢?用反证法很容易证明,这里不详讲)。直线 P1Pn 把点集分成了两部分,即 X 轴上面和下面两部分,分别叫做上包和下包。
2.对上包:求距离直线 P1Pn 最远的点,即下图中的点 Pmax 。
3.作直线 P1Pmax 、PnPmax,把直线 P1Pmax 左侧的点当成是上包,把直线 PnPmax 右侧的点也当成是上包。
4.重复步骤 2、3。
对下包也作类似操作。

然而怎么求距离某直线最远的点呢?我们还是用到解一中的公式:
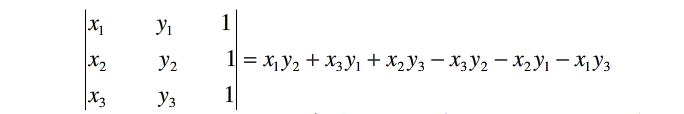
设有一个点 P3 和直线 P1P2 。(坐标:p1(x1,y1),p2(x2,y2),p3(x3,y3))
对上式的结果取绝对值,绝对值越大,则距离直线越远。
注意:在步骤一,如果横坐标最小的点不止一个,那么这几个点都是凸包上的点,此时上包和下包的划分就有点不同了,需要注意。
解三:Jarvis步进法
时间复杂度:O(nH)。(其中 n 是点的总个数,H 是凸包上的点的个数)
思路:
纵坐标最小的那个点一定是凸包上的点,例如图上的 P0。
从 P0 开始,按逆时针的方向,逐个找凸包上的点,每前进一步找到一个点,所以叫作步进法。
怎么找下一个点呢?利用夹角。假设现在已经找到 {P0,P1,P2} 了,要找下一个点:剩下的点分别和 P2 组成向量,设这个向量与向量P1P2的夹角为 β 。当 β 最小时就是所要求的下一个点了,此处为 P3 。

注意:
找第二个点 P1 时,因为已经找到的只有 P0 一个点,所以向量只能和水平线作夹角 α,当 α 最小时求得第二个点。
共线情况:如果直线 P2P3 上还有一个点 P4,即三个点共线,此时由向量P2P3 和向量P2P4 产生的两个 β 是相同的。我们应该把 P3、P4 都当做凸包上的点,并且把距离 P2 最远的那个点(即图中的P4)作为最后搜索到的点,继续找它的下一个连接点。
解四:Graham扫描法
时间复杂度:O(n㏒n)
思路:Graham扫描的思想和Jarris步进法类似,也是先找到凸包上的一个点,然后从那个点开始按逆时针方向逐个找凸包上的点,但它不是利用夹角。

步骤:
把所有点放在二维坐标系中,则纵坐标最小的点一定是凸包上的点,如图中的P0。
把所有点的坐标平移一下,使 P0 作为原点,如上图。
计算各个点相对于 P0 的幅角 α ,按从小到大的顺序对各个点排序。当 α 相同时,距离 P0 比较近的排在前面。例如上图得到的结果为 P1,P2,P3,P4,P5,P6,P7,P8。我们由几何知识可以知道,结果中第一个点 P1 和最后一个点 P8 一定是凸包上的点。
(以上是准备步骤,以下开始求凸包)
以上,我们已经知道了凸包上的第一个点 P0 和第二个点 P1,我们把它们放在栈里面。现在从步骤3求得的那个结果里,把 P1 后面的那个点拿出来做当前点,即 P2 。接下来开始找第三个点:
连接 栈最上面的连个元素(即P0和栈顶)的那个点,得到直线 L 。看当前点是在直线 L 的右边还是左边。如果在直线的右边就执行步骤5;如果在直线上,或者在直线的左边就执行步骤6。
如果在右边,则栈顶的那个元素不是凸包上的点,把栈顶元素出栈。执行步骤4。
当前点是凸包上的点,把它压入栈,执行步骤7。
检查当前的点 P2 是不是步骤3那个结果的最后一个元素。是最后一个元素的话就结束。如果不是的话就把 P2 后面那个点做当前点,返回步骤4。
最后,栈中的元素就是凸包上的点了。
解五:Melkman算法

说真的,这个算法我也还没有看清。网上的资料也少的可怜,我暂且把网上的解释截个图在这里,往后搞懂以后再回来补上。
性能:由一个快排(O(nlogn))和一个遍历找点(O(n)),总体时间复杂度为O(nlogn)。
原理:
点:A(x1,y1),B(x2,y2)
向量AB=(x2-x1,y2-y1)=(x,y)
向量的叉积:a X b =
通过结果的正负判断两矢量之间的顺逆时针关系
l 若a X b > 0,表示a在b的顺时针方向上
l 若a X b < 0,表示a在b的逆时针方向上
l 若a X b == 0,表示a与b共线,但不确定方向是否相同
例如:

A(0,0)
B(2,2)
C(3,1)
D(2,-1)
AB(2,2),AC(3,1),AD(2,-1)
AC X AB = 32-12 = 4>0
AC在AB的顺时针方向上,即点C在向量AB的下面。
实现步骤:
排序:按照x由小到大排序,如果x相同,按照y由小到大排序。
排序之后第一个点必为凸包上的点(证明自己意淫一下,有x最大、x最小、y最小、y最大的点都必在凸包上)。
选最近两个刚入凸包的点,再在排序中依次选点,根据上面所提及到的原理,判断该点在凸包那两点的顺时针还是逆时针方向。
如果在逆时针方向,将该点加入凸包,否则判定出之前进入凸包的点不合格,删除该凸包点,重复第三步,直到该点加入凸包(也就是说每个点都曾进过凸包,只是后来有些被删了)。
以上就是下凸包的构成步骤,上凸包参考下凸包,基本没有什么差别,因为在判断时是判断是否为逆时针,别误以为是在判段该点在向量的下方,上凸包就不可用了,对于逆时针而言都是一样的。
这种方法求出来的点是凸包沿着逆时针方向找出来的,首位相接且第一个点重复两次,所以除了点只有一个的情况下,记得点的个数减一。
备注:对于题目要求求凸包构成的面积时,可以参考以下图示求法:

输入样例解释:
11—散点样例个数
5 8 —散点坐标
12 56
5 2
125 1
15 66
45 77
55 6
45 2
232 5
45 12
54 66
输出样例解释:
tot=7 —构成凸包点的个数
1: 5.00 , 2.00 —沿着凸包逆时针方向,且保留两位小数
2: 125.00 , 1.00
3: 232.00 , 5.00
4: 45.00 , 77.00
5: 15.00 , 66.00
6: 12.00 , 56.00
7: 5.00 , 8.00
//求凸包,时间复杂度nlogn
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
using namespace std;
const int MaxN=10010;
int n,tot;//n为点的个数,tot为凸点的个数
struct point
{
double x,y;
};
point p[MaxN],CHP[MaxN];//CHP为凸包最后所构成的点
bool cmp(point a,point b)//水平排序,按x从大到小排,如果x相同,按y从大到小排序
{
return (a.x<b.x||(a.x==b.x&&a.y<b.y));
}
double xmul(point a,point b,point c)//叉积
{
return (b.x-a.x)*(c.y-a.y)-(b.y-a.y)*(c.x-a.x);
}
void Andrew()
{
sort(p,p+n,cmp);
tot=0;
for(int i=0; i<n; ++i) //计算下半个凸包
{
while(tot>1&&xmul(CHP[tot-2],CHP[tot-1],p[i])<0)
--tot;
CHP[tot++]=p[i];
}
int k=tot;
for(int i=n-2; i>=0; --i) //计算上半个凸包
{
while(tot>k&&xmul(CHP[tot-2],CHP[tot-1],p[i])<0)
--tot;
CHP[tot++]=p[i];
}
if(n>1)//对于只有一个点的包再单独判断
--tot;
}
int main()
{
scanf("%d",&n);
for(int i=0; i<n; ++i)
{
scanf("%lf%lf",&p[i].x,&p[i].y);
}
Andrew();
printf("tot=%d\n",tot);
for(int i=0; i<tot; ++i)
{
printf("%d: %.2lf , %.2lf\n",i+1,CHP[i].x,CHP[i].y);
}
return 0;
}
一些预备知识点:
首先在二维坐标下介绍一些定义:
点:A(x1,y1),B(x2,y2)
向量:向量AB=( x2 - x1 , y2 - y1 )= ( x , y );
向量的模 |AB| = sqrt ( xx+yy );
向量的点积: 结果为 x1x2 + y1y2。
点积的结果是一个数值。
点积的集合意义:我们以向量 a 向向量 b 做垂线,则 | a | * cos(a,b)为 a 在向量 b 上的投影,即点积是一个向量在另一个向量上的投影乘以另一个向量。且满足交换律
应用:可以根据集合意义求两向量的夹角,
cos(a,b) =( 向量a * 向量b ) / (| a | * | b |) = (x1x2 + y1y2) / (| a | * | b |)
向量的叉积: 结果为 x1y2-x2y1
叉积的结果也是一个向量,是垂直于向量a,b所形成的平面,如果看成三维坐标的话是在 z 轴上,上面结果是它的模。
方向判定:右手定则,(右手半握,大拇指垂直向上,四指右向量a握向b,大拇指的方向就是叉积的方向)
叉积的集合意义:1:其结果是a和b为相邻边形成平行四边形的面积。
2:结果有正有负,有sin(a,b)可知和其夹角有关,夹角大于180°为负值。
3:叉积不满足交换律
应用:
1:通过结果的正负判断两矢量之间的顺逆时针关系
若 a x b > 0表示a在b的顺时针方向上
若 a x b < 0表示a在b的逆时针方向上
若 a x b == 0表示a在b共线,但不确定方向是否相同