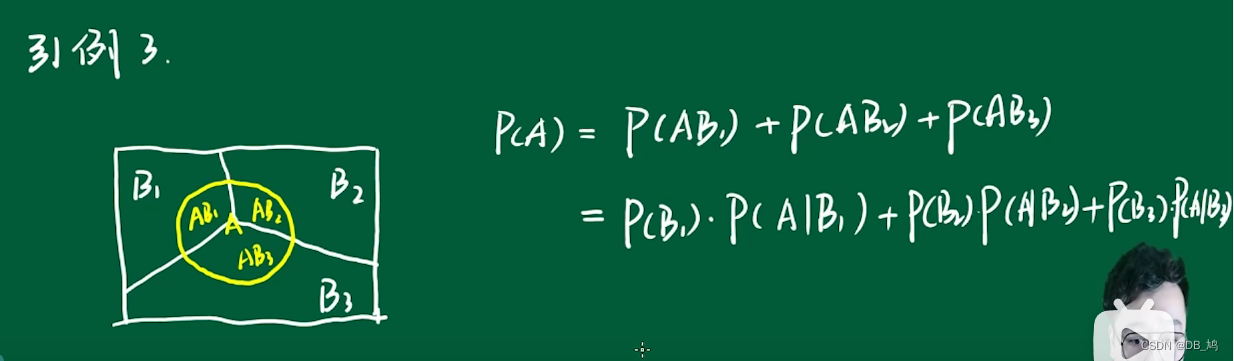全概率与贝叶斯公式
全概率
之前有说过全概率,某件事A可能会在不同的情况下有不同的概率发生,这些情况相互独立,讲这些概率加和即为全概率。
例如:
高数挂科(10%)的前提下,概率挂科的概率为60%;
高数不挂科(90%)的前提下,概率挂科的概率为5%;
则概率挂科的全概率为:10% * 60% + 90% * 5%
总结:全概率公式为: P ( A ) = ∑ i = 1 n P ( B i ) ∗ P ( A ∣ B i ) P(A) = \sum_{i=1}^nP(B_i) * P(A|B_i) P(A)=∑i=1nP(Bi)∗P(A∣Bi)
贝叶斯公式
与全概率公式相反的就是贝叶斯公式
用来求一件事发生之后是属于某种情况的概率,本质上是一个条件概率
P ( B i ∣ A ) = P ( A B i ) P ( A ) = P ( B i ) P ( A ∣ B i ) ∑ i = 1 n P ( B i ) ∗ P ( A ∣ B i ) P(B_i|A) = \frac{P(AB_i)}{P(A)} = \frac{P(B_i)P(A|B_i)}{\sum_{i=1}^nP(B_i) * P(A|B_i)} P(Bi∣A)=P(A)P(ABi)=∑i=1nP(Bi)∗P(A∣Bi)P(Bi)P(A∣Bi)
例题
解题步骤:
- 用符号设出概率
- 求全概率
- 利用贝叶斯公式求条件概率
基础例题1
基础例题2
事件独立性
定义
某个事件是否收到其他事件的影响称为事件的独立性。
定义式: P ( A B ) = P ( A ) P ( B ) P(AB) = P(A)P(B) P(AB)=P(A)P(B)
结论
-
下面这些命题是等价的
- 如果AB两个事件独立
- P ( A B ) = P ( A ) P ( B ) P(AB) = P(A)P(B) P(AB)=P(A)P(B)
- P ( B ) = P ( B ∣ A ) , P ( A ) > 0 P(B) = P(B|A) ,P(A) > 0 P(B)=P(B∣A),P(A)>0
- P ( B ∣ A ) = P ( B ∣ A ˉ ) , P ( A ) ≠ 0 , P ( A ) ≠ 1 P(B|A) = P(B|\bar A),P(A)\not=0,P(A)\not=1 P(B∣A)=P(B∣Aˉ),P(A)=0,P(A)=1
- P ( A ∣ B ) = P ( A ∣ B ˉ ) , P ( B ) ≠ 0 , P ( B ) ≠ 1 P(A|B) = P(A|\bar B),P(B)\not=0,P(B)\not=1 P(A∣B)=P(A∣Bˉ),P(B)=0,P(B)=1
-
如果A与B相互独立
那么 A 与 B ˉ A与\bar B A与Bˉ, A ˉ 与 B \bar A与B Aˉ与B, A ˉ 与 B ˉ \bar A与\bar B Aˉ与Bˉ都相互独立 -
如果 P ( A ) > 0 , P ( B ) > 0 P(A)>0,P(B)>0 P(A)>0,P(B)>0
那么A与B相互独立,A与B互不相容不能同时成立- 相互独立指两个事件不共用一个样本空间
- 互不相容指在同一个样本空间中两件事不能同时发生
-
必然事件、不可能事件与任何事件都相互独立
例题
基础例题