树的存储结构
1、 双亲表示法(顺序存储结构)
优点:求双亲容易
缺点:求孩子困难

2、链式存储结构
孩子表示法:将树中的每个结点的孩子结点排列成一个线性表,用链表存储起来。对于含有 n 个结点的树来说,就会有 n 个单链表,将 n 个单链表的头指针存储在一个线性表中,这样的表示方法就是孩子表示法。
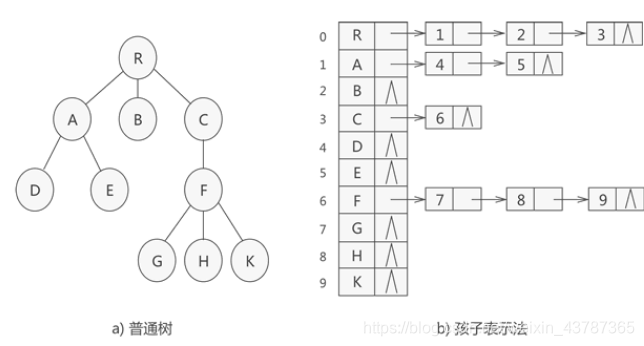
孩子双亲表示法:
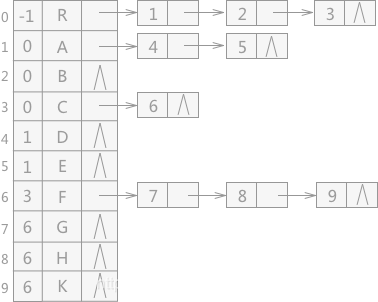
2. 孩子兄弟表示法
1、又称二叉链表表示法,即以二叉链表作为树的存储结构
2、结点的两个链域分别指向该结点的第一个孩子结点和下一个兄弟结点。

左手牵自己的孩子,右手牵兄弟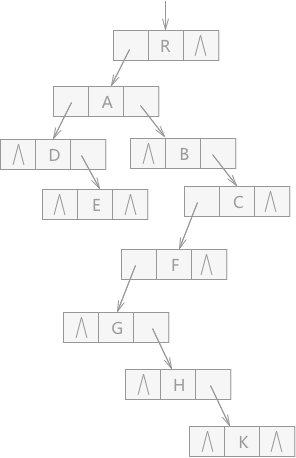
转换
- 树转换为二叉树
树中每个结点最多只有一个最左边的孩子(长子)和一个右邻的兄弟。
按照这种关系很自然地就能将树转换成相应的二叉树:
1.在所有兄弟结点之间加一连线
2.对每个结点,除了保留与其长子的连线外,去掉该结点与其它孩子的连线。
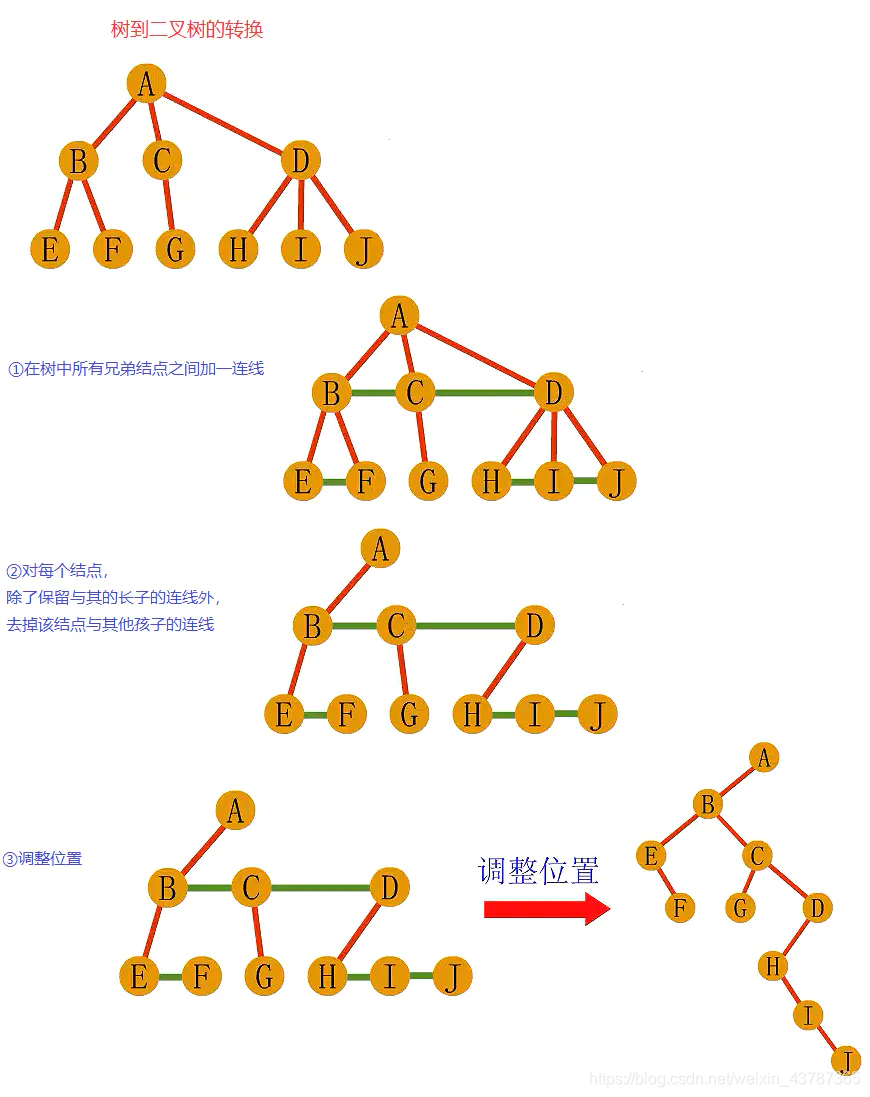
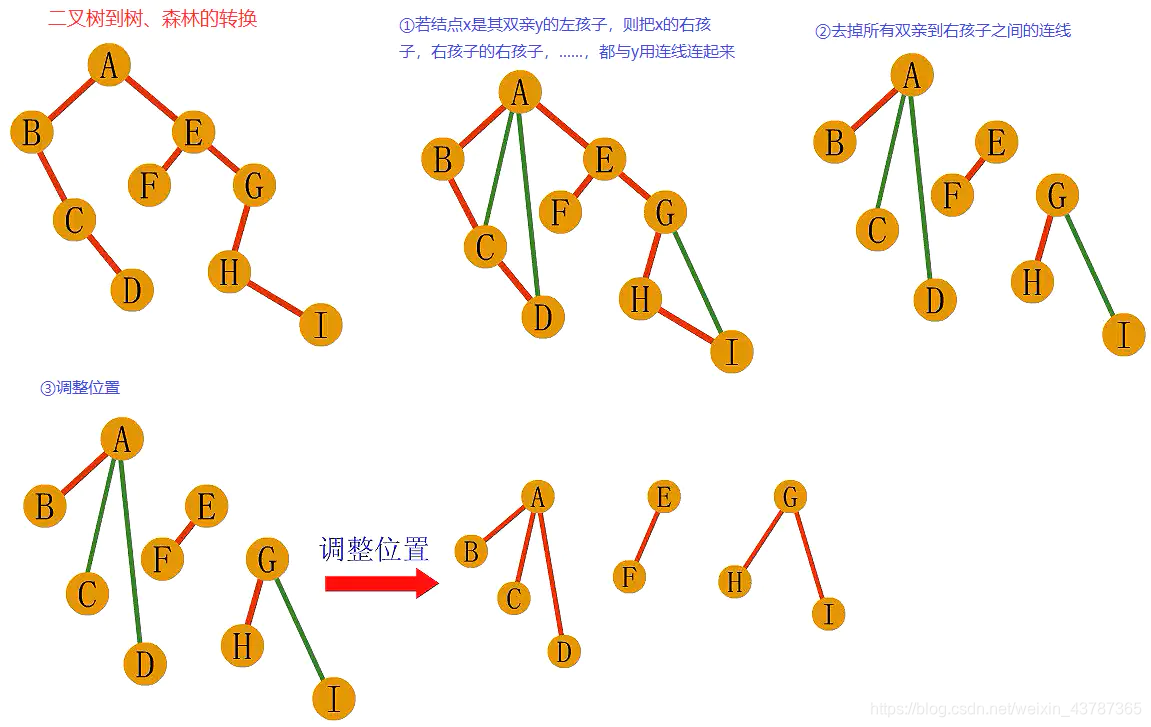
- 二叉树转换为树/森林
- 加线。
若某结点X的左孩子结点存在,则将这个左孩子的右孩子结点、右孩子的右孩子结点、右孩子的右孩子的右孩子结点…,都作为结点X的孩子。将结点X与这些右孩子结点用线连接起来。
2.去线。删除原二叉树中所有结点与其右孩子结点的连线。
- 森林转换为二叉树
1.把每棵树转换为二叉树。
2.第一棵二叉树不动,从第二棵二叉树开始,依次把后一棵二叉树的根结点作为前一棵二叉树的根结点的右孩子,用线连接起来。

例题: 将森林转换为对应的二叉树,若在二叉树中,结点u是结点v的父结点的父结点, 则在原来的森林中, u和v可能具有的关系是(B)
I. 父子关系 II. 兄弟关系
III. u 的父结点与 v 的父结点是兄弟关系
A. 只有 II
B. I 和 II
C. I 和 III
D. I、II 和 III
解析:
森林与二又树的转换规则为“左孩子右兄弟”。在最后生成的二叉树中,父子关系在对应森林关系中可能是兄弟关系或原本就是父子关系。
情形Ⅰ:若结点v是结点u的第二个孩子结点,在转换时,结点v就变成结点u第一个孩子的右孩子,符合要求。
情形Ⅱ:结点u和v是兄弟结点的关系,但两者之中还有一个兄弟结点k,则转换后,结点v就变为结点k的右孩子,而结点k则是结点u的右孩子,符合要求。
情形Ⅲ:结点v的父结点是原先的父结点或兄弟结点。若结点u的父结点与v的父结点是兄弟关系,则转换之后,不可能出现结点u是结点v的父结点的父结点。
例:设森林F对应的二叉树为B,它有m个结点,B的根为p,p的右子树结点个数为n,森林F中的第一棵树的结点个数是(A).
A、m-n
B、m-n-1
C、n+1
D、条件不足,无法确定。
解析:
二叉树中的左子树和根结点是原森林的第一棵树,其余结点来自于森林的其他子树,其他树的结点为n,则第一棵树的结点个数为m-n。
例:已知一棵有2011个结点的树,其叶结点个数为116, 该树对应的二叉树中无右孩子的结点个数是(D)
A. 115
B. 116
C. 1895
D. 1896
解析:
特殊解法
一颗前面1895个结点只有一个孩子的树,最后面节点有116个叶子结点,这样没有兄弟的结点只有1895个,但是最后一个叶子结点也没有右孩子,所以是1895+1=1896
例:假设:森林F有15条边,25个结点
那么:森林F中包含树的个数是(C)
A. 8
B. 9
C. 10
D. 11
解析:
根据一棵树的边数+1=结点数。
1棵树时,边数 = 结点数-1
2棵树时,边数 = 结点数-2
….
n棵树时,边数 = 结点数-n
于是得到:25-15 = 10.
遍历
树的遍历
- 先序遍历:先访问树的根结点,然后再依次先根遍历根的每棵子树(根左右)。
- 后序遍历:先依次遍历每棵子树(左右根),然后再访问根结点。

森林的遍历
森林的遍历也分为先序遍历和后序遍历,其实就是按照树的先根遍历和后根遍历依次访问森林的每一棵树。
树、森林与二叉树的共性:
树、森林的前根(序)遍历和二叉树的前序遍历结果相同;
树、森林的后根(序)遍历和二叉树的中序遍历结果相同!