
机器学习模型的创建就如同在一个山谷里漫步,我们的平面坐标就是模型,我们的海拔就是损失函数值。我们希望找到一个最优的模型使得损失最小,即找到这个山谷的最低点。
我们有以下几种策略:
策略1:随机选坐标,试Loss值
不解释,显然很差。
策略2:如同在山谷中下山一样,顺着斜坡往下走
自然地引出了导数的概念:只要沿着导数方向调整模型,即可获得朝着最优下降方向下降的损失值。(局部最优暂时不提)
在多维函数里,导数变为梯度(Gradiant),由微积分知识,可导函数梯度最大的相反方向即为函数值下降最快的方向。
所以沿着梯度的方向不断按固定步长调整模型值,即可逐渐趋近一个最优的模型。
对于一个模型如向量W:

上面采用对每一个参数微调求得相应梯度的方法,然而此方法极差,因为一个W可以有成千上万的维度,若求成千上万次才最终对模型进行一步的微调,效率可见会极低。
更换思路:既然损失函数也是一个函数,我们可以采用微积分的思想,直接寻找该损失函数对于模型W每一个维度的梯度计算公式,计算梯度时直接代值,计算速度会快很多。

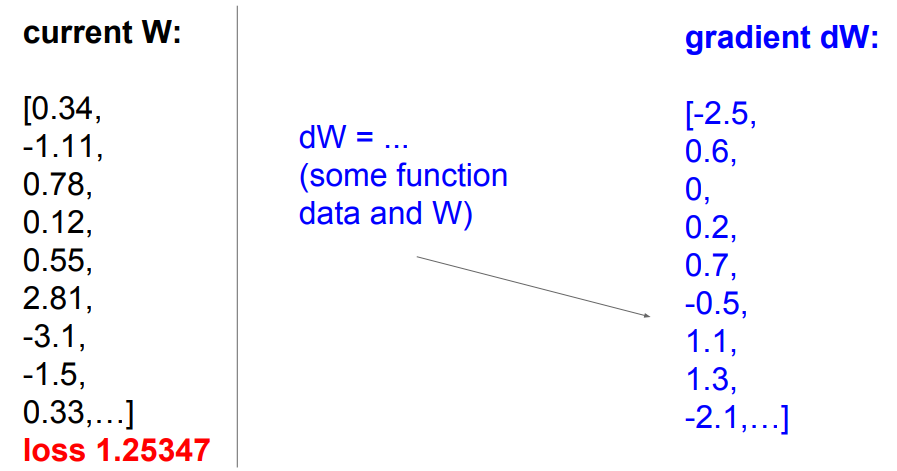
注:实际操作中总是使用公式法(解析法)计算梯度,然而在调试中检查计算梯度的公式是否正确时时可以采用分段数值法进行debug。
梯度下降法优化的代码如下:

step_size是一个超参数(调试时最先修改的参数),2式取负号是因为梯度计算公式是算的梯度最大的方向,按梯度下降的方向是其反方向。
另外,损失函数是一个求和均值,所以损失函数的梯度也是一个均值表达式。

实际中的数据量N可能非常大以至于无法用所有数据来进行梯度计算,所以可以采用随机抽样法,抽取固定数量的数据作为数据集(如256个)
