在上学期的数据结构课中,我已经接触了很多树的类型,比如二叉查找树,红黑树,平衡二叉树等。我的身边有一本《算法竞赛进阶指南》一书,在里面我又了解到了线段树、字典树等内容,尤其是线段树引起了我的兴趣。线段树解决的问题很简单,比如有一个序列,{32,15,6,125,522,57,45...123,555},长度为n,接下来有m个询问,每一次的询问都会给出一个区间(l,r),使得这个区间内,所有的数都加x,或者求出这个区间内的总值。问题十分简洁易懂,如果放在大一时,我会毫不犹豫地写两个for,第一层for 1->m,表示m个询问;第二层for l->r,表示区间加数或求和,显而易见,时间复杂度为O(nm),在时间苛刻的情况下,并不属于一个好方法。
线段树当然是一棵树,我喜欢用结构体来存储节点信息,一个节点的必要信息有这个节点表示的范围(l,r),这个节点的编号k(因为线段树是一棵二叉树,所以它有二叉树的性质,由此可得如果一个父节点的编号为k,则它的两个子节点编号分别为k<<1,k<<1|1)。
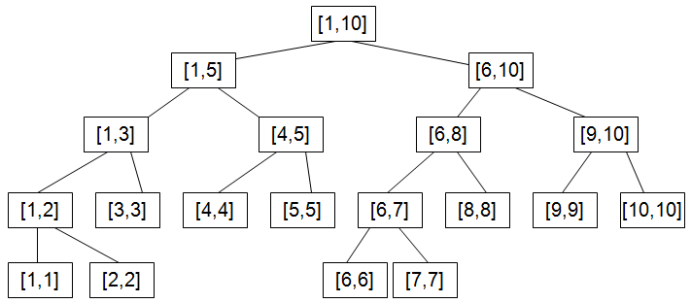
当这棵树递归建完后,可以得到上图的结构。对于每一个父节点而言,都表示整个序列中的一段子区间;对于每个叶子节点而言,都表示序列中的单个元素信息;子节点不断向自己的父亲节点传递信息,而父节点存储的信息则是他的每一个子节点信息的整合。
有没有觉得很熟悉?对,线段树就是分块思想的树化,或者说是对于信息处理的二进制化——用于达到O(logn)级别的处理速度,log以2为底。(其实以几为底都只不过是个常数,可忽略)。而分块的思想,则是可以用一句话总结为:通过将整个序列分为有穷个小块,对于要查询的一段区间,总是可以整合成k个所分块与m个单个元素的信息的并(0<=k,m<=sqrt(n))(0<=k,m<= n)。但普通的分块不能高效率地解决很多问题,所以作为log级别的数据结构,线段树应运而生。
有了线段树这个数据结构后,最开始提到的区间修改的问题就可以解决了。但还可以再优化。对于区间操作,我们考虑引入一个名叫“lazytag”(懒标记)的东西——之所以称其“lazy”,是因为原本区间修改需要通过先改变叶子节点的值,然后不断地向上递归修改祖先节点直至到达根节点,时间复杂度最高可以到达O(nlogn)的级别。但当我们引入了懒标记之后,区间更新的期望复杂度就降到了O(logn)的级别且甚至会更低。这个标记独立存在于每个节点,记录每次、这个节点要更新的值,当某个区间要被修改时,区间的公共祖先的lazy记录了此次更新的值,当下一次要询问此区间的总和时,再向下更新这个lazy就行了,这样某些不会再被访问到的区间没有做过多的操作,又省了很多时间。
线段树的扩展性很好,可以做很多事情,求和、求积、求余、位运算等等,只要搞清它的原理,灵活运用剪枝技巧,就很好拓展,这也是线段树相较于其它解决区间问题的数据结构(比如树状数组、treap)的优势。但是缺点也是很突出,空间复杂度较高,扩展性好的同时代码量较大,比较臃肿。因此,在解决此类问题的时候,要分析需求和条件,选用合适的算法。