线段树算法总结&专题训练4(可持久化线段树/主席树)
一些 update
update 2020/12/28:感谢本机房 lxh 大佬指出的问题,主席树建空树的时候我们应该是对离散化后的数组建空树而不是直接对 a a a 数组建空树,对各位读者造成的影响深表歉意,现已更正。
update 2020/12/29:最近在学习 FHQ Treap 的时候发现自己把『动态开点』和『静态开点』的意义弄混了,『动态开点』是用于指针上的,在我的写法中只能说是『静态开点』,对各位读者造成的影响深表歉意,现已更正。如果还有一些地方的『动态开点』没有改成『静态开点』,请私信作者,不胜感激!
update 2020/12/29:修改了一下『总结』板块,将所有线段树的总结放在了这里,因为可能学『吉司机线段树』与『李超线段树』还要等一段时间,因此先写下总结,对各位读者的影响深表歉意。
回顾
在 线段树算法总结&专题训练3 中我们见识了 GSS1-5 的题目如何用线段树解决,那么现在就让我们看一看由线段树引申的算法——主席树(可持久化线段树)。
那么闲话不多说,开始吧!
1.概述
1.可持久化是个啥?
首先让我们看看『可持久化』是什么意思。
在之前我们做到的线段树的所有题目中,我们都是针对当前的线段树直接修改/查询,但是有这样一类题目:它要求在第 k k k 次操作后进行修改,查询,这种问题就是『可持久化』。
接下来先说明一些名词及解释:
- 『历史版本/版本』:指在某一次修改/查询之后 我们将修改/查询之后的线段树看作一棵新的线段树,将这棵线段树视作某一『历史版本/版本』上的值。比如现在有一个初始版本的线段树,编号为 0。然后我们执行一次单点修改之后将新的线段树视作一个新的『历史版本/版本』,将其存下,编号为 1。这个解释同样适用于别的东西,比如某个数组中某个位置的值。此时同样可以使用『历史版本/版本』来描述。
- 不过:当使用『历史版本』来讲述的时候我们指的是严格意义上的『历史版本』,表明可能会对多个之前的『版本』操作,但是使用『版本』来讲述的时候可能只是单纯的对最新生成的『版本』操作。
- 『生成版本』:指在修改/查询之后 我们将修改/查询之后的线段树 存到一个新的数组中,为其开辟一个新的『历史版本/版本』的过程叫做『生成版本』。
- 『版本的根(节点)』:指在某一『版本』中这棵线段树的根节点。
- 『复制版本』:将某一『版本』复制并且『生成一个新的版本』(即生成版本),复制后新的『版本』与原『版本』的线段树 一摸一样。
- 『在可持久化下』:表明这个操作是会对『历史版本』进行操作的,可能涉及到『生成版本』、『复制版本』。
是不是被上面这些东西吓晕了qwq,其实只要能够深入的理解,其实还是简单的。
那么现在我们回过头看看『可持久化』。
可持久化的问题在上面已经讲述,显然不能直接用线段树来做。
比如这两道题。
2.模板。
题单:
2.可持久化怎么做?
这道题有两个操作:在可持久化下单点修改,在可持久化下单点查询。
去掉『在可持久化下』几个字,我相信各位能很快的写出代码。
那么加上了『在可持久化下』这几个字,我们又要怎么做呢?
很简单啊!直接对每一个版本存一棵完整的线段树,询问哪个版本就用哪个版本,生成版本时直接复制整棵线段树即可。
话说直接用数组他不香吗
空间限制:你是不是当我傻qwq。
这个思想还是比较重要的,因为他会帮助我们思考如何建立可持久化线段树。
显然这种做法没有问题,但是会导致 MLE。
因此我们要考虑空间优化。
3.空间要如何优化?
首先我们看看这棵呆萌的线段树。(为了方便直接拿圆圈当区间了)
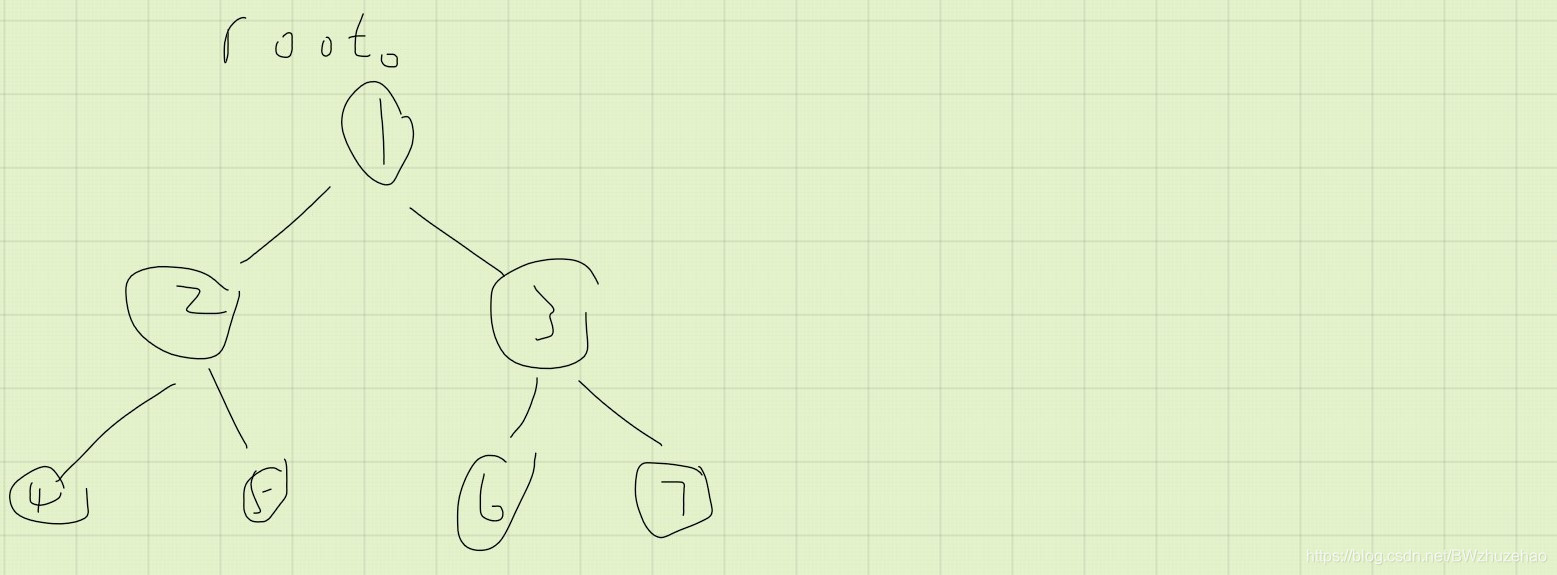
图中的 r o o t 0 root_0 root0 表示初始版本(也就是第一个版本)的根节点。
那么此时假如我们要修改 a 2 a_2 a2 要怎么办呢?
a 2 a_2 a2 对应 5 号叶子节点。
那么我们想一想:是不是只有 1-2-5 这条路径上的点要改动,别的点不需要动啊?
因此我们可以新开几个节点,这些节点是改动的点,那么没改动的点怎么办呢?直接连接到原先的节点上不就好了?
如下图:
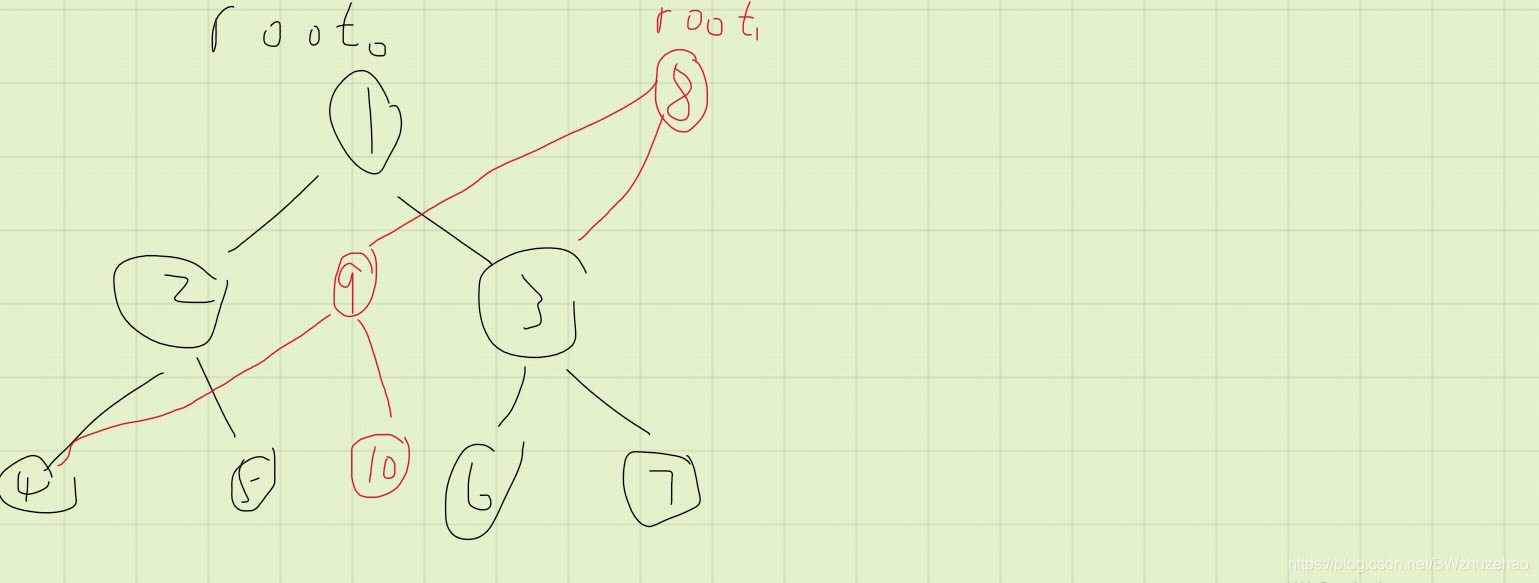
此时你会惊奇的发现:我们只需要生成 3 个节点:10 号节点对应修改后的 5 号节点,9 号节点对应修改后的 2 号节点,8 号节点对应修改后的 1 号节点,此时我们需要生成一个新的版本,这个版本的根节点是 8 号节点,而这棵线段树由 8,9,3,4,10,6,7 组成。
所以可持久化线段树的一个重要思想就是:需要的时候新开节点,不需要的时候就共用节点。
下文称『新开节点』为『静态开点』。
观察图,我们会再次发现:每次我们只需要开 log 2 n \log_2n log2n 个节点即可,完美降低空间复杂度。
但是很遗憾的是,因为我们有动态开点操作,所以我们不能跟普通线段树那样用 p < < 1 , p < < 1 ∣ 1 p << 1, p << 1 | 1 p<<1,p<<1∣1 来表示左右儿子,而是需要在结构体内维护 l s , r s ls,rs ls,rs 来表示左右儿子。
那么假如我们接下来有这么几个操作:
- 在版本 1 上修改 a 3 a_3 a3。
- 在版本 0 上修改 a 1 a_1 a1。
建议各位自己画一画,如果画出来了就说明已经掌握。
答案如图所示(图很丑,不喜勿喷):
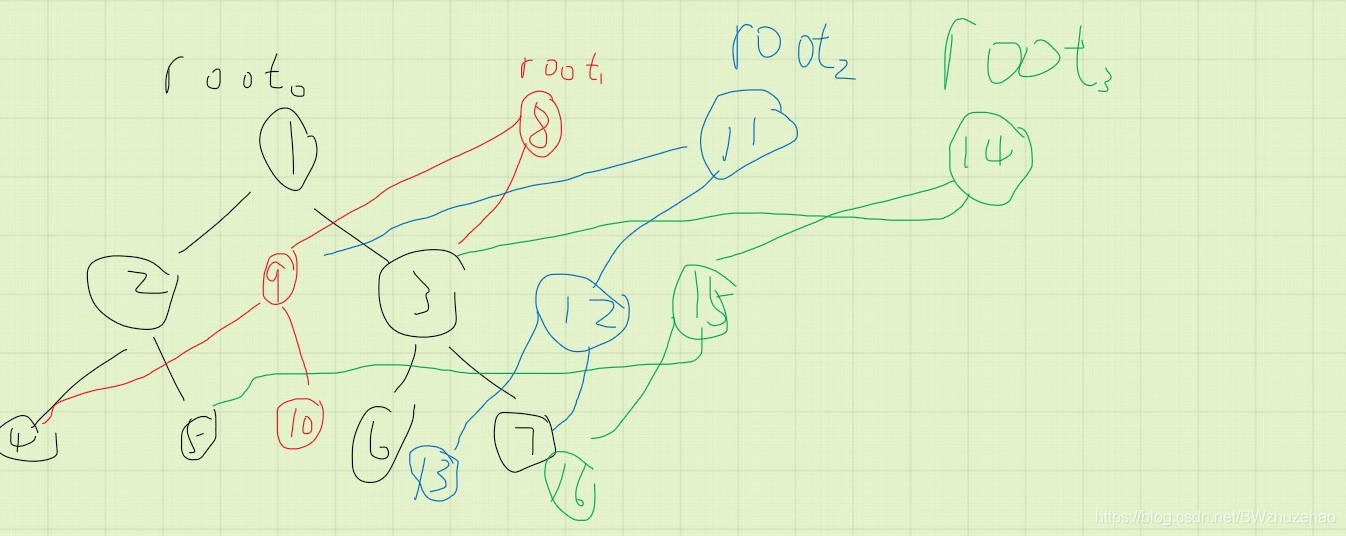
你画对了吗?
那么现在我们做一个查询操作:查询版本 2 中 a 2 a_2 a2 的值。
首先这是一个单点查询问题,按照线段树的套路我们先找到版本 2 的根节点 11 号节点,然后单点查询,最后查到的是 10 号节点。
但是我们还要复制版本啊?
也很简单,我们直接指定 r o o t 4 root_4 root4 为 r o o t 2 root_2 root2 不就好了?如下图:
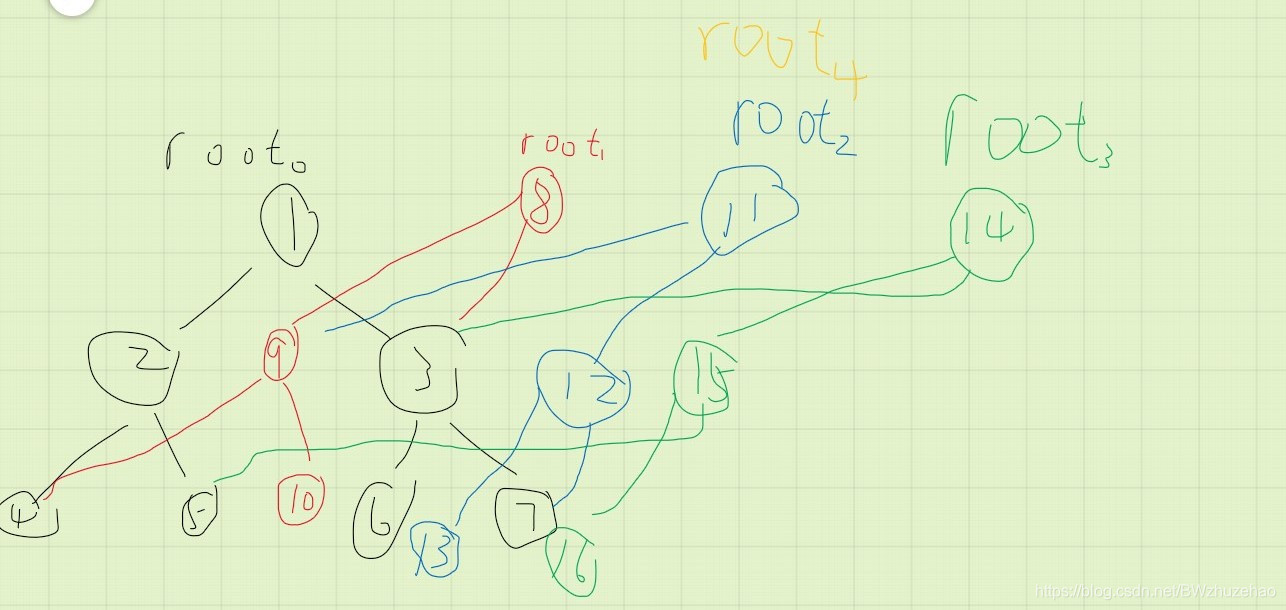
所以这就是主席树的全部思路。
4.代码又要怎么写?
首先考虑到有静态开点操作,因此我们先设一个 c n t cnt cnt 表示节点个数。
0.如何存树
代码:
struct node
{
int ls, rs, val;//ls -> 左儿子, rs -> 右儿子, val -> 值
}tree[(MAXN << 4) + (MAXN << 2)];//注意空间要开到 20 倍左右
为什么没有 l , r l,r l,r 了?因为实际上我们在 change,ask \operatorname{change,ask} change,ask 中是可以传两个参数 l = 1 , r = n l=1,r=n l=1,r=n ,然后二分执行的,也就是说不需要存下 l ( p ) , r ( p ) l(p),r(p) l(p),r(p) ,而这种写法在可持久化线段树里面会显得更加简洁(其实普通线段树也差不多)。
1.建树操作-build
代码:
int build(int p, int l, int r)//注意返回值是 int, 不是 void, 我们需要知道每个节点的左右儿子是谁
{
p = ++cnt;//静态开点
if (l == r) {
tree[p].val = a[l]; return cnt;}//这里不适合用 v(p) 这样的东西表示,写着写着就明白了
int mid = (l + r) >> 1;
tree[p].ls = build(tree[p].ls, l, mid);//确定左儿子编号
tree[p].rs = build(tree[p].rs, mid + 1, r);//确定右儿子编号
return p;//返回节点编号
}
2.单点修改-change
代码:
int change(int p, int l, int r, int loc, int val)//还是注意返回值,因为我们有静态开点操作
{
tree[++cnt] = tree[p];//先复制一份节点,可以复制下左右儿子,对于不修改的点可以自动保留左右儿子信息
p = cnt;//更新节点
if (l == r) tree[p].val = val;//到了叶子节点
else
{
int mid = (l + r) >> 1;
if (loc <= mid) tree[p].ls = change(tree[p].ls, l, mid, loc, val);//单点修改,注意修改左右儿子信息
else tree[p].rs = change(tree[p].rs, mid + 1, r, loc, val);
}
return p;//不要忘记返回当前节点编号
}
3.单点查询-ask
代码:
int ask(int p, int l, int r, int loc)//这里不需要静态开点了,但是我们需要返回答案
{
if (l == r) return tree[p].val;//叶子节点返回值
int mid = (l + r) >> 1;
if (loc <= mid) return ask(tree[p].ls, l, mid, loc);//继续找答案
else return ask(tree[p].rs, mid + 1, r, loc);
}
4.最后的代码是啥?
如下:(其实主要注意 main \operatorname{main} main 函数,别的上面已经贴过了)
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1e6 + 10;
int n, m, a[MAXN], root[MAXN], cnt;
struct node
{
int ls, rs, val;//ls -> 左儿子, rs -> 右儿子, val -> 值
}tree[(MAXN << 4) + (MAXN << 2)];//注意空间要开到 20 倍左右
int read()
{
int sum = 0, fh = 1; char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-') fh = -1; ch = getchar();}
while (ch >= '0' && ch <= '9') {
sum = (sum << 3) + (sum << 1) + (ch ^ 48); ch = getchar();}
return sum * fh;
}
int build(int p, int l, int r)//注意返回值是 int, 不是 void, 我们需要知道每个节点的左右儿子是谁
{
p = ++cnt;//静态开点
if (l == r) {
tree[p].val = a[l]; return cnt;}//这里不适合用 v(p) 这样的东西表示,写着写着就明白了
int mid = (l + r) >> 1;
tree[p].ls = build(tree[p].ls, l, mid);//确定左儿子编号
tree[p].rs = build(tree[p].rs, mid + 1, r);//确定右儿子编号
return p;//返回节点编号
}
int change(int p, int l, int r, int loc, int val)//还是注意返回值,因为我们有静态开点操作
{
tree[++cnt] = tree[p];//先复制一份节点,可以复制下左右儿子,对于不修改的点可以自动保留左右儿子信息
p = cnt;//更新节点
if (l == r) tree[p].val = val;//到了叶子节点
else
{
int mid = (l + r) >> 1;
if (loc <= mid) tree[p].ls = change(tree[p].ls, l, mid, loc, val);//单点修改,注意修改左右儿子信息
else tree[p].rs = change(tree[p].rs, mid + 1, r, loc, val);
}
return p;//不要忘记返回当前节点编号
}
int ask(int p, int l, int r, int loc)//这里不需要静态开点了,但是我们需要返回答案
{
if (l == r) return tree[p].val;//叶子节点返回值
int mid = (l + r) >> 1;
if (loc <= mid) return ask(tree[p].ls, l, mid, loc);//继续找答案
else return ask(tree[p].rs, mid + 1, r, loc);
}
int main()
{
n = read(); m = read();
for (int i = 1; i <= n; ++i) a[i] = read();
root[0] = build(0, 1, n);//处理初始版本
for (int i = 1; i <= m; ++i)
{
int v = read(), opt = read(), loc = read();
if (opt == 1)
{
int val = read();
root[i] = change(root[v], 1, n, loc, val);//生成最新版本,第 2,第 3 个参数是区间,相当于之前的 l(p),r(p)
}
else
{
printf("%d\n", ask(root[v], 1, n, loc));
root[i] = root[v];//不要忘记复制版本!!!!!!
}
}
return 0;
}
现在你已经学会了可持久化线段树 1 ——可持久化数组。
现在让我们看一下可持久化线段树 2 ——主席树。
6.主席树又是个啥?
主席树最经典的应用就是区间第 k k k 大,他的玩法与可持久化数组完全不一样。
对主席树的一些名词的解释:
- 『历史版本/版本』:表示我们在 建立主席树的过程中生成的每一棵树,将这些称之为版本。
- 『生成版本』:建立主席树的过程中 我们新建一棵树。
- 『版本的根(节点)』:同上。
- 『复制版本』:同上。
- 『在可持久化下』:同上。
- 『静态开点』:同上。
如果你看过上面的解释就会发现:等等,我们难道在建立主席树的时候要建立多棵线段树吗?
是的。在建立主席树的过程中我们需要建立多棵线段树,且我们依然需要通过可持久化数组的方式优化空间,具体见下文。
7.主席树要怎么做?
主席树的一个思想就是:将普通的建树操作转换成若干个单点修改操作,在值域上建树。 因此主席树维护的区间就变成了值域区间,有一点值域分块的感觉。
首先我们依然不考虑如何优化节点,而是拆成若干棵线段树。
比如现在有这样一组数据:4 3 1 5 8 7 6 2 3。
首先插入 4,根据我们之前说的,做一次单点修改操作,修改 a 4 a_4 a4 加 1。
那么线段树如下所示:
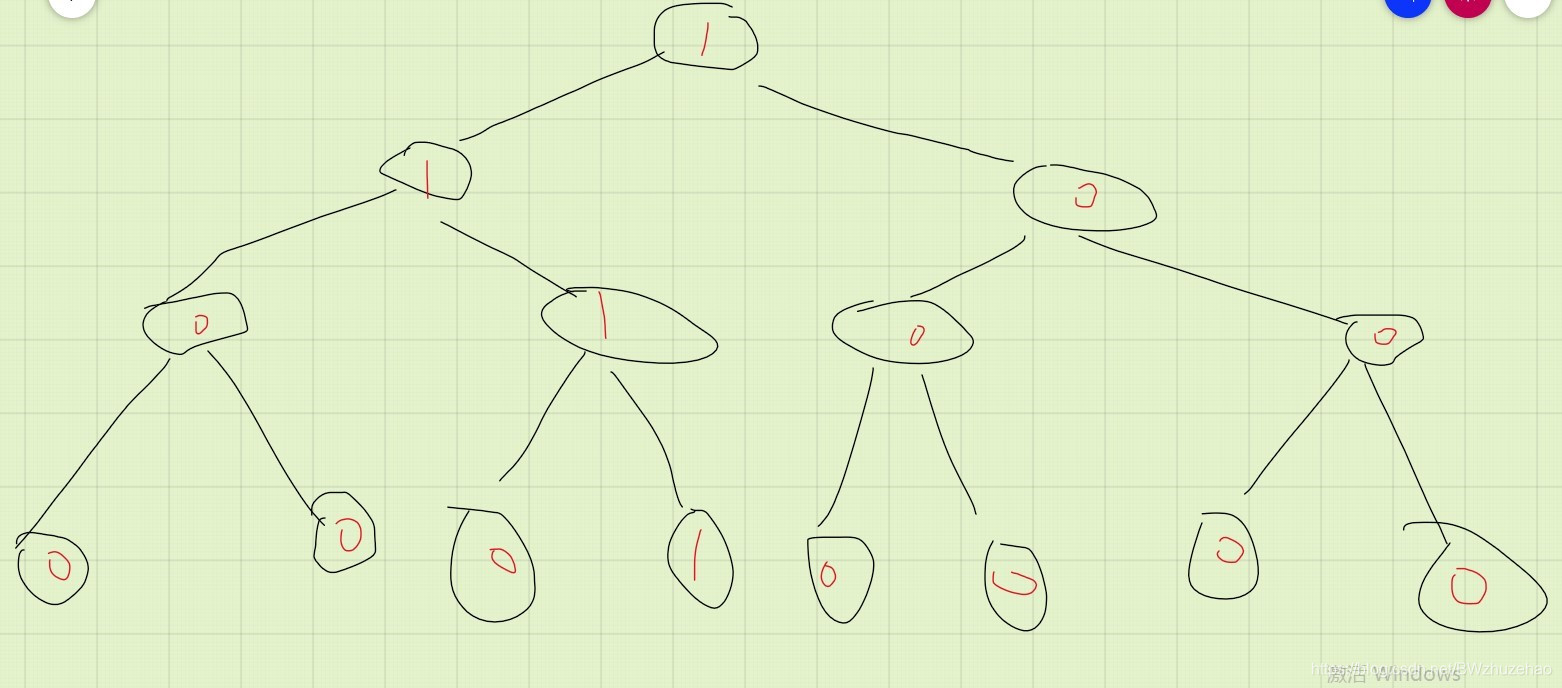
其实通过这一步你就会发现,实质上主席树维护的是 值在 [ l , r ] [l,r] [l,r] 内的树的个数。
那么现在我们再插入 3,如下所示:
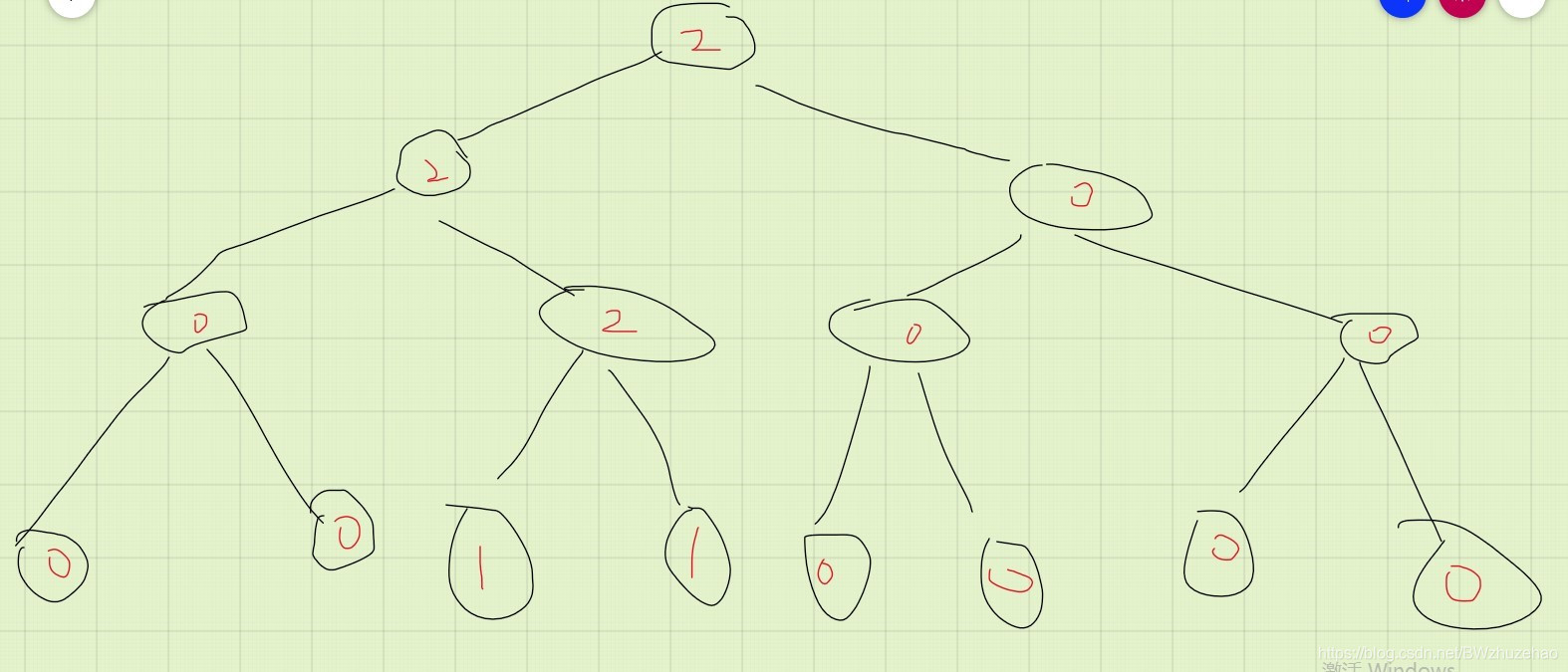
那么根据上述两个操作,你应该已经看懂了主席树的操作。
接下来一次性全部插入 1 5 8 7 6 2(注意没有最后一个 3),各位可以画一画,画对说明基础操作掌握了。
答案 :
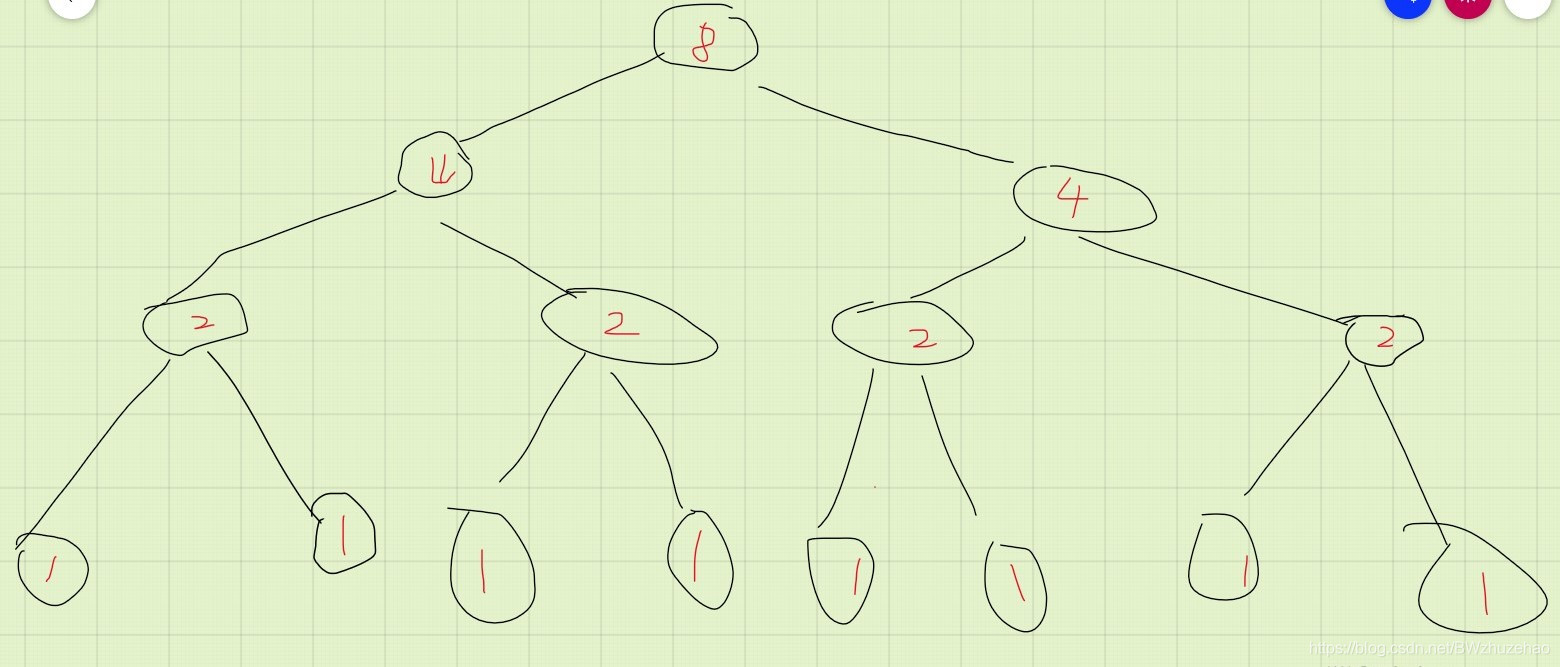
于是我们最后插入 3,得到了这样一棵线段树:

那么假如我们要求 [ 3 , 8 ] [3,8] [3,8] 内的第 5 大呢?
那么首先将这线段树取出来(特别注意:这两棵线段树分别是第 2 次和第 8 次的线段树,具体为什么是 2 而不是 3 后面会详细讲解):


然后我们做一次 对应节点相减 操作,可以得到下面一棵线段树:

那么让我们看看第 5 大怎么求。
首先我们发现根节点左边有 2 个数,右边有 4 个数,第 5 大应该在右边,因此我们跑到右子树上,同时由于前面 2 个数被我们省略了,因此我们实质要求右子树的第 3 大。
然后现在左子树 2 个数,右子树 2 个数,那么我们还是要跑右子树上,这样就变成了求右子树上的第 1 大。
最后左子树 1 个数,右子树 1 个数,我们跑到左子树上,仍然求第 1 大。
此时到了叶子节点,返回值即可。
因此对于求区间 [ l , r ] [l,r] [l,r] 的第 k k k 大,我们可以总结出如下步骤:
- 首先取出两棵线段树的根节点,知道这是哪两棵线段树。
- 然后我们同时从根节点开始遍历,将左儿子对应值相减得到一个数 x x x。
- 如果 x < k x<k x<k ,说明此时左边的数都不是第 k k k 大,我们需要往右子树跑,但是不要忘记更新 k = k − x k = k - x k=k−x ,因为此时右子树上求的已经不是第 k k k 大!
- 否则往左子树跑,还是求第 k k k 大。
- 如果到了叶子节点,那么返回答案。
那么为什么就是对的呢?
8.主席树为啥正确?
首先我们从主席树的构造方式就可以看出来:我们本质上是模仿前缀和建了一棵前缀线段树。
那么对于 [ l , r ] [l,r] [l,r] 区间,我们同样模仿前缀和让第 r r r 棵线段树减去第 l − 1 l-1 l−1 棵线段树就可以得到 [ l , r ] [l,r] [l,r] 区间内数值的信息。
所以此时我们就得到了一棵正确的线段树。
由于主席树在值域上建树,因此我们可以通过上面的方法找到第 k k k 大。
9.空间要如何优化?
还记得可持久化数组是怎么干的吗?好像是『静态开点』,相同节点连边来着?
那么我们现在也这么干不就好了~
此时我们就需要模仿可持久化数组静态开点,将每一次插入数值转化成单点修改,将每一棵线段树视作一个『版本』,不断『生成版本』即可。
10.代码又要如何写?
0.树的结构体
代码:
struct node
{
int ls, rs, sum;//左儿子编号,右儿子编号,值
}tree[(MAXN << 4) + (MAXN << 2)];//记得开 20 倍空间
1.建树操作-build
实质上,主席树的建树是建一棵空树,确定版本 0,这样做是因为如果查询 [ 1 , x ] ( x ∈ [ 2 , n ] ) [1,x](x \in [2,n]) [1,x](x∈[2,n]) 的第 k k k 大我们需要一棵空树。
代码:
int build(int p, int l, int r)//建树操作
{
p = ++cnt;//静态开点
if (l == r) return p;//叶子节点返回
int mid = (l + r) >> 1;
tree[p].ls = build(tree[p].ls, l, mid);//建立左子树
tree[p].rs = build(tree[p].rs, mid + 1, r);//建立右子树
return p;//返回节点编号
}
2.单点修改-change
代码:
int change(int p, int l, int r, int x)//单点修改
{
int rt = ++cnt;//静态开点
tree[rt] = tree[p]; tree[rt].sum++;//复制节点且 sum++
int mid = (l + r) >> 1;
if (l == r) return rt;//叶子节点返回编号
if (x <= mid) tree[rt].ls = change(tree[p].ls, l, mid, x);//单点修改建立左子树
else tree[rt].rs = change(tree[p].rs, mid + 1, r, x);//单点修改建立右子树
return rt;//返回编号
}
3.查询操作-ask
代码:
//p1 为左边线段树的编号,p2 为右边线段树的编号,l,r 是区间
int ask(int p1, int p2, int l, int r, int k)//查询操作
{
if (l == r) return l;//叶子节点返回值
int sum = tree[tree[p2].ls].sum - tree[tree[p1].ls].sum, mid = (l + r) >> 1;//确定差值
if (sum >= k) return ask(tree[p1].ls, tree[p2].ls, l, mid, k);//往左子树跑
else return ask(tree[p1].rs, tree[p2].rs, mid + 1, r, k - sum);//往右子树跑,不要忘记是 k - sum 而不是 k!
}
11.最后的代码是啥?
注意这题需要离散化。
代码:
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 2e5 + 10;
int n, m, a[MAXN], b[MAXN], cntn, root[MAXN], cnt;
struct node
{
int ls, rs, sum;//左儿子编号,右儿子编号,值
}tree[(MAXN << 4) + (MAXN << 2)];//记得开 20 倍空间
int read()
{
int sum = 0, fh = 1; char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-') fh = -1; ch = getchar();}
while (ch >= '0' && ch <= '9') {
sum = (sum << 3) + (sum << 1) + (ch ^ 48); ch = getchar();}
return sum * fh;
}
int build(int p, int l, int r)//建树操作
{
p = ++cnt;//静态开点
if (l == r) return p;//叶子节点返回
int mid = (l + r) >> 1;
tree[p].ls = build(tree[p].ls, l, mid);//建立左子树
tree[p].rs = build(tree[p].rs, mid + 1, r);//建立右子树
return p;//返回节点编号
}
int change(int p, int l, int r, int x)//单点修改
{
int rt = ++cnt;//静态开点
tree[rt] = tree[p]; tree[rt].sum++;//复制节点且 sum++
int mid = (l + r) >> 1;
if (l == r) return rt;//叶子节点返回编号
if (x <= mid) tree[rt].ls = change(tree[p].ls, l, mid, x);//单点修改建立左子树
else tree[rt].rs = change(tree[p].rs, mid + 1, r, x);//单点修改建立右子树
return rt;//返回编号
}
//p1 为左边线段树的编号,p2 为右边线段树的编号,l,r 是区间
int ask(int p1, int p2, int l, int r, int k)//查询操作
{
if (l == r) return l;//叶子节点返回值
int sum = tree[tree[p2].ls].sum - tree[tree[p1].ls].sum, mid = (l + r) >> 1;//确定差值
if (sum >= k) return ask(tree[p1].ls, tree[p2].ls, l, mid, k);//往左子树跑
else return ask(tree[p1].rs, tree[p2].rs, mid + 1, r, k - sum);//往右子树跑,不要忘记是 k - sum 而不是 k!
}
int main()
{
n = read(); m = read();
for (int i = 1; i <= n; ++i) b[i] = a[i] = read();
sort(b + 1, b + n + 1);
cntn = unique(b + 1, b + n + 1) - (b + 1);//离散化
root[0] = build(1, 1, cntn);//建空树
for (int i = 1; i <= n; ++i)
{
a[i] = lower_bound(b + 1, b + cntn + 1, a[i]) - b;//离散化
root[i] = change(root[i-1], 1, cntn, a[i]);//将数列转化成单点修改
}
for (int i = 1; i <= m; ++i)
{
int l = read(), r = read(), k = read();
int p = ask(root[l - 1], root[r], 1, cntn, k);//区间查询,注意是 l - 1 不是 l!
printf("%d\n", b[p]);
}
return 0;
}
3. 练习题
先咕了。
4.总结
这里总结一下可持久化数组与主席树的相同点与不同点。
相同点:全部都采用静态开点的形式,连接到已知节点上省略空间。
不同点:可持久化数组在序列上建树,主席树在值域上建树。