作者:刘亮
幻方(Magic Square)是一种将数字安排在正方形格子中,使每行、列和对角线上的数字和都相等的方法。
幻方也是一种中国传统游戏。旧时在官府、学堂多见。它是将从一到若干个数的自然数排成纵横各为若干个数的正方形,使在同一行、同一列和同一对角线上的几个数的和都相等。
三阶幻方
本篇主聊高阶幻方构造方法的java实现
数据结构:以二维数组存放数字
例:上面的三阶幻方数组数据如下(不考虑幻方阶次较高,最大值超过int最大值)
int[][] square = {
{8,1,6},
{3,5,7},
{4,9,2}
};数据结构有了,怎么去验证一个二阶数组的数据是不是一个有效的幻方构造数据呢?
具体思路就是反证法,默认数据符合幻方数据内容:
/**验证一个二阶数组里的数是不是符合一个幻方的要求*/
public static boolean isValidSquare(int[][] nums){
try {
//i阶次幻方
int i = nums.length;
//行列斜的和为
int s = (i*i+1)*i/2;
//数据完整性校验数组
int[] check = new int[i*i+1];
//校验每一行/每一列的和是不是等于s
for (int x = 0; x < i; x++) {
int lineSum = 0;
int colSum = 0;
for (int y = 0; y < i; y++) {
check[nums[x][y]]=nums[x][y];
lineSum += nums[x][y];
colSum += nums[y][x];
}
if (lineSum!=s || colSum!=s) {
return false;
}
}
//校验两个对角线的和是否等于s
int s1Sum = 0;
int s2Sum = 0;
for (int x = 0; x < i; x++) {
s1Sum += nums[x][x];
s2Sum += nums[i-x-1][x];
}
if (s1Sum!=s || s2Sum!=s) {
return false;
}
//校验check数组中是否包含1到i*i中的每一个数
for (int j = 0; j < check.length; j++) {
if (j!=check[j]) {
return false;
}
}
} catch (Exception e) {
e.printStackTrace();
//默认符合幻方规则,任意数组越界等错误都认为是不合格的数据
return false;
}
return true;
}
下面开讲n(>=3)阶幻方的构造及实现
奇数阶幻方
拉-卢贝尔算法
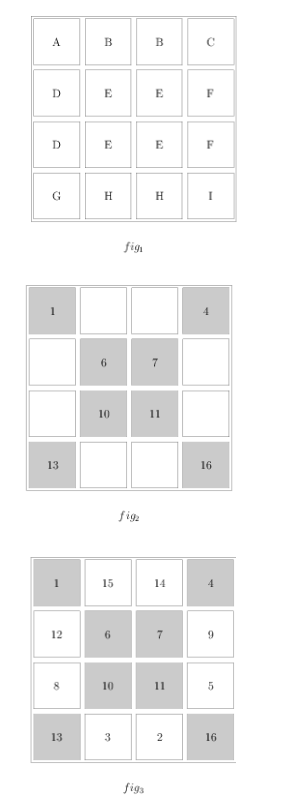
这个算法又称“阶梯法”。算法如下:
- 将1置于第一行中间。
- 将下一个数字置于当前数字的右上角。如果已经处于方阵的边界,则放在方阵的对边(如图1中的2和4)。
- 若出现下面两种情况,则将下一个数字放于当前数字的下方:
①当前位置的右上角已经有一个数字(如图2中的6和11)。
②当前位置已经是方阵的右上方(如图2中的16)。
- 结束,如下图3:


Java实现:
/**
* k=2*n+1
* 拉-卢贝尔算法
* 阶梯法
*/
public static int[][] getSquare2k1LenF1(int k) throws Exception{
int[][] res = new int[k][k];
int x = 0;
int y = k/2;
int total = k*k;
for (int i = 1; i <= total; i++) {
res[x][y] = i;
int m = (x-1+k)%k;
int n = (y+1)%k;
if (res[m][n]>0) {
x = (x+1)%k;
}else{
x= m;
y= n;
}
}
return res;
}
菱形算法
另一种由康韦(J.H.Conway)建立的算法被称为“菱形算法”,步骤如下(以5x5为例):
- 从左边中间开始,将奇数在方阵内填成一个菱形。
- 将方阵分成5条对角线,每条对角线上有5个方格。如果图1所示。
- 从第一条对角线开始将偶数填入剩余的空格内,图2中填满了前两条对角线。
- 结束,如图3。



Java实现:
/**
* 菱形算法
* k=2*n+1
*/
public static int[][] getSquare2k1LenF2(int k) throws Exception{
int[][] res = new int[k][k];
//初始化奇数空间
int n = k/2;
//奇数起点坐标
int baseX = n,baseY = 0;
//起点走向,true向右 false向下
boolean type = true;
//奇数计数
int count = 1;
//当前奇数坐标
int x = baseX;
int y = baseY;
while(true){
res[x][y] = count;
count = count+2;
x--;y++;
if (y>=x-n && y<=x+n) {
}else{
if (type) {
baseY++;
}else{
baseX++;
}
type = !type;
if (baseX==k-1 && baseY==n+1) {
break;
}
x = baseX;
y = baseY;
}
}
//偶数起点坐标
int baseP = -1;
int baseQ = n+1;
//起点走向,true向右 false向下
type = false;
//偶数计数
count = 2;
//当前奇数坐标
int p = baseP;
int q = baseQ;
while(true){
p = (p+k)%k;
q = (q+k)%k;
res[p][q] = count;
count = count+2;
p = (p-1+k)%k;
q = (q+1)%k;
if (res[p][q]!=0) {
if (type) {
baseQ++;
}else{
baseP++;
}
type = !type;
if (baseP==n && baseQ==k) {
break;
}
p = baseP;
q = baseQ;
}
}
return res;
}
杨辉法
九子斜排 上下对易 左右相更 四维挺出 戴九履一 左三右七 二四为肩 六八为足
举个例子:9个数斜着排,上下的两个数1,9,左右的两个数3,7互相换一下,四个角上的2,4,6,8就移到那四个角上去,这样就填好了一个三阶幻方了.

再给一个7阶的构造填数过程,具体规则大家自己揣摩

Java实现:
/**
* 九子斜排 上下对易 左右相更 四维挺出 戴九履一 左三右七 二四为肩 六八为足
* k=2*n+1
*/
public static int[][] getSquare2k1LenF3(int k) throws Exception{
int[][] res = new int[k][k];
//初始构造一个菱形空间
int[][] dia = new int[2*k-1][2*k-1];
//把1到k*k个数填入菱形空间
for (int i = 1; i <= k*k; i++) {
//计算i在菱形空间的坐标
//批次
int p = (i+(k-1))/k;
//偏移量
int q = i%k==0?k:i%k;
q--;
dia[p-1+q][k-p+q] = i;
}
//填充中心
int m = (k-1)/2;
for (int i = m; i <m+k ; i++) {
for (int j = m; j < m+k; j++) {
if (dia[i][j]==0) {
if (i<j) {
if(i+j<2*k-1){
dia[i][j] = dia[i+k][j];
}else{
dia[i][j] = dia[i][j-k];
}
}else{
if (i+j<2*k-1) {
dia[i][j] = dia[i][j+k];
}else{
dia[i][j] = dia[i-k][j];
}
}
}
//往结果集赋值
res[i-m][j-m] = dia[i][j];
}
}
return res;
}
单偶数阶幻方
侓克斯算法
这个算法也是由康韦给出的。思想是将方阵分成多个2x2的小方阵,小方阵按照位置分成L、U、X三种类型。然后在大体上按照卢-拉贝尔算法来走,在每个小方阵中根据小方阵的类型来填数。具体算法如下:
- 将方阵分成(2i+1)个(2x2)的小方阵,小方阵的分类这样确定:前i+1行是L类型,后面一行是U类型,最后的i-1行是X类型,然后交换第i+1行和第i+2行中间小方阵的类型。对于10x10的方阵如图1。
- L、U、X的填法如图2。
- 最终结果如图3。


Java实现:
/**
* k=4*n+2
* 侓克斯算法
*
* L: 4 1 U: 1 4 X: 1 4
* 2 3 2 3 3 2
*
* 前i+1行是L类型,后面一行是U类型,最后的i-1行是X类型,然后交换第i+1行和第i+2行中间小方阵的类型
*/
public static int[][] getSquare4k2LenF1(int k) throws Exception{
int[][] res = new int[k][k];
int x = 0;
int y = k/2-1;
int total = k*k/4;
for (int i = 1; i <= total; i++) {
//定型
//1:L 0:U -1:X
int type = 1;
if ((x== k/2+1 && y!=k/2-1) || (x==k/2-1 && y==k/2-1)) {
type = 0;
}
if (x>= k/2+3) {
type = -1;
}
//填充
switch (type) {
case 1:
res[x][y] = 4*i;
res[x][y+1] = 4*i-3;
res[x+1][y] = 4*i-2;
res[x+1][y+1] = 4*i-1;
break;
case 0:
res[x][y] = 4*i-3;
res[x][y+1] = 4*i;
res[x+1][y] = 4*i-2;
res[x+1][y+1] = 4*i-1;
break;
default:
res[x][y] = 4*i-3;
res[x][y+1] = 4*i;
res[x+1][y] = 4*i-1;
res[x+1][y+1] = 4*i-2;
break;
}
//定位
int m = (x-2+k)%k;
int n = (y+2)%k;
if (res[m][n]>0) {
x = (x+2)%k;
}else{
x= m;
y= n;
}
}return res;
}
加法算法
将一个幻方加上另外一个幻方所得的和仍然具有幻方的特性,只是可能会有重复项,这是幻方的加法特性。下面的方法就是根据这个特性设计的,首先建立两个方阵A、B,具有幻方的特性(横、纵、斜和相同),然后让A加上B的i倍,就得到一个幻方。假如我们要作一个4i+2阶幻方(此处以14为例)。具体算法如下:
先作一个14(4i+2)阶的方阵A,这个方阵分成4个7(2i+1)阶小方阵,每个小方阵是一个奇数阶的幻方,奇数阶幻方构造方法已经有了。如图1。
- 先作一个14(4i+2)阶的方阵A,这个方阵分成4个7(2i+1)阶小方阵,每个小方阵是一个奇数阶的幻方,奇数阶幻方构造方法已经有了。如图1。
- 再作一个14(4i+2)阶的方阵B,这个方阵只由0、1、2、3构成,具体作法如下:
①第一列:3(i)个3,4(i+1)个0,5(i+2)个2,2(i-1)个1
②前7(2i+1)列与都与第一列相同,只有第4(i+1)列例外,该列第一个3和第一 个0交换位置。
③后7(2i+1)列与前7(2i+1)列相同,不过3和0交换,1和2交换。
④结果如图2。
- 构造幻方C=A+i2B。如图3,C即所求。



Java实现:
/**
* 加法算法
* k=4*n+2
*/
public static int[][] getSquare4k2LenF2(int k) throws Exception{
int[][] res = new int[k][k];
//幻方A初始化
int[][] sA = new int[k][k];
int[][] temp = getSquare2k1LenF1(k/2);
for (int i = 0; i < k; i++) {
for (int j = 0; j < k; j++) {
sA[i][j] = temp[i%(k/2)][j%(k/2)];
}
}
//幻方B初始化
int[][] sB = new int[k][k];
int n = (k-2)/4;
for (int i = 0; i < k; i++) {
for (int j = 0; j < k; j++) {
if (i<k/2 && j<n || i>=k/2 && j>=n && j<k/2) {
sB[i][j]=3;
}
if(i<k/2 && j>=k/2 && j<3*n+3 || i>=k/2 && j>=3*n+3){
sB[i][j]=2;
}
if (i<k/2 && j>=3*n+3 || i>=k/2 && j>=k/2 && j<3*n+3) {
sB[i][j]=1;
}
}
}
sB[n][0] = 0;
sB[n][n] = 3;
sB[3*n+1][0] = 3;
sB[3*n+1][n] = 0;
//幻方A和幻方B相加
//RES = A + B*k*k/4
for (int i = 0; i < k; i++) {
for (int j = 0; j < k; j++) {
res[i][j] = sA[i][j]+sB[i][j]*k*k/4;
}
}
return res;
}
双偶数阶幻方
分割算法
- 将方阵分成16个小方阵,如图1。
- 先在A、C、E、G、I方阵中填入数字,其他方阵跳过,如图2。
- 再逆序(从右下往左上)赶往余下的数字,如图3。
- 结束,如图3
下面是一个8次的方阵:

Java实现:
/**
* k=4*n
* 分割算法
*/
public static int[][] getSquare4kLenF1(int k) throws Exception{
int[][] res = new int[k][k];
//分割数据临时数组
int[] temp = new int[k*k/2];
int index = 0;
//预填充
for (int i = 0; i < k; i++) {
for (int j = 0; j < k; j++) {
//符合分割条件
int m = i%4;
int n = j%4;
if (m!=n && m+n!=3) {
temp[index++] = i*k+j+1;
res[i][j]= 0;
}else{
res[i][j] = i*k+j+1;
}
}
}
//分割出的数据排序
Arrays.sort(temp);
int tempIndex = temp.length-1;
//再填充
for (int i = 0; i < k; i++) {
for (int j = 0; j < k; j++) {
if (res[i][j]==0) {
res[i][j] = temp[tempIndex--];
}
}
}
return res;
}
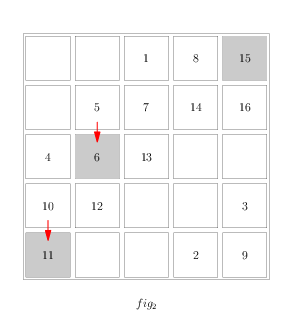
对角线算法
- 将数字顺序填入方阵内,如图1。
- 将方阵分成四个相同大小的方阵。并找出每个小方阵的对角线,如图1阴影部分。
- 将阴影部分旋转180度,如图2。

Java实现:
/**
* 对角线算法
* k=4*n
*/
public static int[][] getSquare4kLenF2(int k) throws Exception{
int[][] res = new int[k][k];
for (int i = 0; i < k; i++) {
for (int j = 0; j < k; j++) {
//坐标i,j是否处在对角线规则内
int m = i%4;
int n = j%4;
if (m==n || m+n==3) {
res[i][j] = (k-1-i)*k+(k-1-j)+1;
}else{
res[i][j] = i*k+j+1;
}
}
}
return res;
}
