Efficient Zero-Knowledge Argument for Correctness of a Shuffle学习笔记（1）

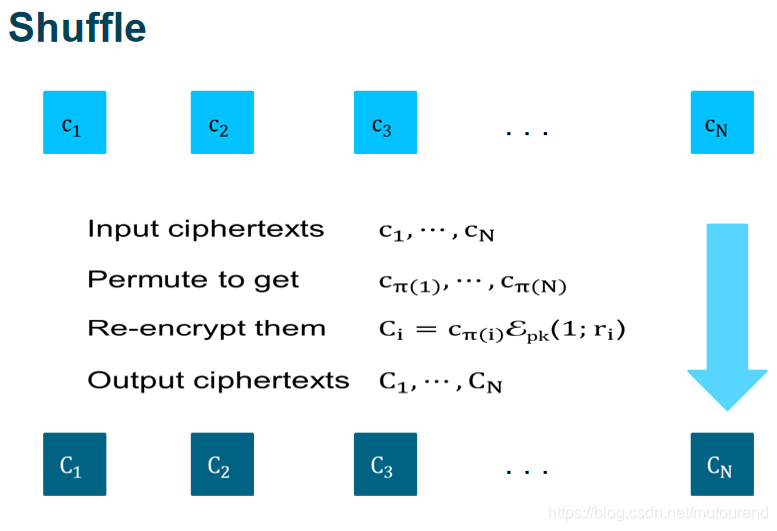
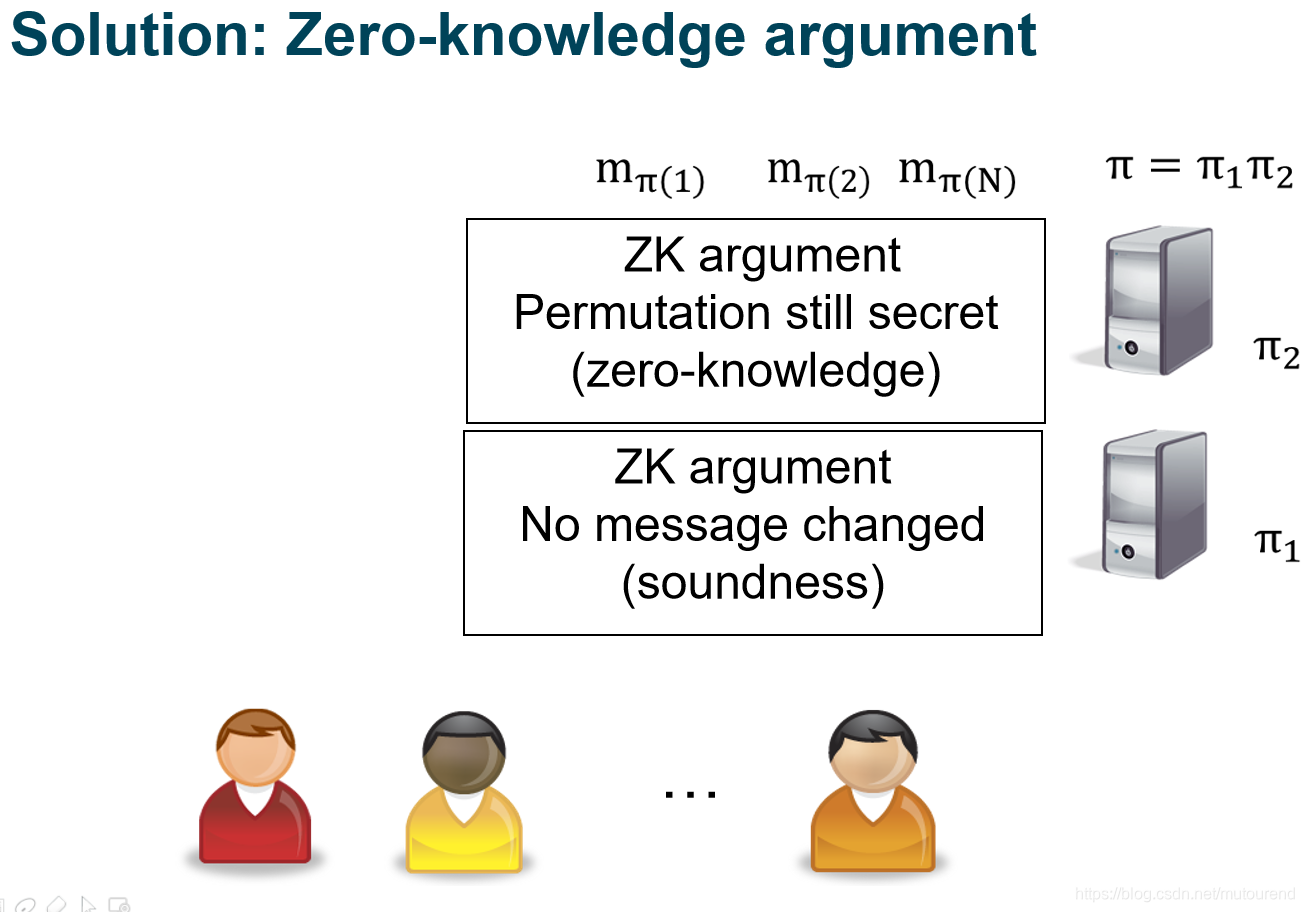
Stephanie Bayer和Jens Groth 2012年论文《Efficient Zero-Knowledge Argument for Correctness of a Shuffle》。
该论文中主要针对e-voting mix-net构建中用到的shuffle homomorphic encryption场景，提出了an honest verifier zero-knowledge argument for the correctness of a shuffle of homomorphic encryptions 算法，该算法在prove和verify the correctness of a shuffle of 100,000 ElGamal ciphertexts用时均在2分钟左右。

1. 背景知识

• 本论文的argument具有sublinear communication complexity，当shuffle $N(=m\times n)$ ciphertexts时，需要传送 $O(m+n)$ group elements 且若 $m=n$则最小的communication complexity 为 $O(\sqrt{N})$。
• prover的computational complexity为 $O(N\log{m})$ exponentiations for constant round arguments或者 若允许logarithmic number of rounds的话， prover的computational complexity可为 $O(N)$ exponentiations。
• verifier的计算比较轻量。
• 构建full shuffle argument的基础为：Neff’s approach [Nef01] is based on the invariance of polynomials under permutation of the roots，即Nef01的shuffle算法基于的是：多项式的根permutation的话，其最终形成的多项式是不变的—— $f(x)=(x-r_1)(x-r_2)...(x-r_n)$。
• 引入了multi-exponentiation argument，用于hide committed values。
• 基于hidden committed values的shuffle argument。与[Gro09]类似，做了些微改进。
• 主要是利用了EIGamal encryption的乘法同态性和Pedersen commitment的加法同态性。所以需要构建相应的common reference string $\sigma =(pk,ck)$， $pk$为EIGamal encryption的public keys， $ck$为Pedersen commitment的commitment key，两者可以基于不同的group实现，但是要求具有相同的prime order $q$。

其中EIGamal的知识详见：博客 EIGamal encryption VS Pairing encryption。

1. EIGamal具有乘法同态性：
   
2. Pedersen commitment具有加法同态性：
   
   
   

2. Shuffle argument

需要an argument of knowledge of permutation $\pi\in \sum_{N}$ and randomness $\{\rho_i\}_{i=1}^N$ such that for given ciphertexts $\{C_i\}_{i=1}^N$, $\{C_i^{'}\}_{i=1}^N$ we have $C_i^{'}=C_{\pi(i)} \varepsilon_{pk}(1;\rho_i)$。
Shuffle argument由multi-exponentiation argument和product argument组成：

• multi-exponentiation argument：用于证明the product of a set of ciphertexts raised to a set of committed exponents yields a particular ciphertext。
• product argument：用于证明a set of committed values has a particular product。

主要的实现步骤为：

1. Prover对permutation进行commit，即commit to $\pi(1),…,\pi(N)$。【第一组commitment】
2. Verifier给Prover challenge $x$。
3. Prover commit to $x^{\pi(1)},…,x^{\pi(N)}$。【第二组commitment】
4. Prover提供argument，证明其知道相应的openings of the commitments to permutations of respectively $1,…,N$和 $x^1,…,x^N$，同时证明这两组commitment采用的是相同的permutation。【即第二组commitment是对 $x^1,…,x^N$ permuted in an order that was fixed before the prover saw $x$】。

• 4.1 为了证明两组commitment采用的是相同的permutation，Verifier给Prover random challenges $y$和 $z$。
• 4.2 Prover commit to 一系列 $d_1-z=y\pi(1)+x^{\pi(1)}-z,…,d_N-z=y\pi(N)+x^{\pi(N)}-z$。使用product argument，即可证明 $\prod_{i=1}^{N}(d_i-z)= \prod_{i=1}^{N}(yi+x^i-z)$等式成立。【想象其为 $z$的N阶多项式， $d_i$是对其root根 $yi+x^i$的permute，基于Schwartz-Zippel lemma可知，针对特定的 $z$值Prover伪造找到相应 $d_i$值使该等式成立的概率不高于 $\frac{N}{q-1}$，可忽略。同理，针对 $y$值，Prover伪造两组commitment使等式成立的概率也可忽略。】

5. Prover使用multi-exponentiation argument来证明存在 $\rho$值，使得$ $\prod_{i=1}^{N}C_i^{x^i}=\varepsilon_{pk}(1;\rho)\prod_{i=1}^{N}(C_i^’)^{x^{\pi(i)}}$等式成立。即可实现基于密文 $C_i，C_i^’$的shuffle证明，而Verifier不知道具体的permutation规则。
   

详细的shuffle argument算法流程为：

3. Multi-exponentiation Argument

将第二节shuffle argument算法流程中的 $\vec{a},\vec{b}$向量表示为N=n*m矩阵。
其中的multi-exponentiation argument可表示为：

简化描述，假设 $\rho=0$，public info: $\vec{C_1},...,\vec{C_m},C$，witness: $\vec{a_1},...,\vec{a_m}$，需要证明： $C=\prod_{i=1}^{m}\vec{C_i}^{\vec{a_i}}$。
基本流程为：

1. Prover依次对 $\vec{a_1},...,\vec{a_m}$进行commit，将相应的 $\vec{c_A}=(com_{ck}(\vec{a_1};r_1),...,com_{ck}(\vec{a_m};r_m))$发送给verfier
2. Prover计算 $E_k=\prod_{1\leq i,j\leq m;j=(k-m)+i}\vec{C_i}^{\vec{a_j}}$，将相应的 $E_1,E_2,...,E_{2m-1}$发送给Verifier【其中 $E_m=C$】。
3. Verifier给Prover challenge $x$。
4. Prover计算 $\vec{a}=\sum_{j=1}^{m}x^j\vec{a_j}$，将相应的向量 $\vec{a}$发送给verifier。
5. Verifier验证 $C^{x^m}\prod_{k=1;k\neq m}^{2m-1}E_k^{x^k}=\prod_{i=1}^{m}\vec{C_i}^{(x^{m-i}\vec{a})}$成立，则可证明 $C=\prod_{i=1}^{m}\vec{C_i}^{\vec{a_i}}$成立。相应的理论依据为： $\prod_{i=1}^{2m-1}E_k^{x^k}=\prod_{i=1}^{m}\vec{C_i}^{(x^{m-i}\sum_{j=1}^{m}x^j\vec{a_j})}=\prod_{i=1}^{m}\vec{C_i}^{(x^{m-i}\vec{a})}=C^{x^m}\prod_{k=1;k\neq m}^{2m-1}E_k^{x^k}=C^{x^m}\prod_{k=1;k\neq m}^{2m-1}{\prod_{1\leq i,j\leq m;j=(k-m)+i}\vec{C_i}^{\vec{a_j}x^k}}=C^{x^m}\prod_{i=1}^{m}{\vec{C_i}}^{\sum_{1\leq j\leq m;k=m-i+j;k\neq m}\vec{a_j}x^k}$，于是有： $C^{x^m}=\prod_{i=1}^{m}{\vec{C_i}}^{(x^{m-i}\sum_{j=1}^{m}x^j\vec{a_j}-\sum_{1\leq j\leq m;k=m-i+j;k\neq m}\vec{a_j}x^k)}=\prod_{i=1}^{m}{\vec{C_i}}^{\vec{a_i}x^m}=(\prod_{i=1}^{m}{\vec{C_i}}^{\vec{a_i}})^{x^m}$，从而有： $C=\prod_{i=1}^{m}\vec{C_i}^{\vec{a_i}}$成立。【注意，原论文有的公式有点typo。】

以上流程，可能存在witness泄露的来源点有：
1）为了防止在rewind 第3和第4步时，Verifier用不同的challenge $x$从Prover那获取不同的 $\vec{a}=\sum_{j=1}^{m}x^j\vec{a_j}$，从而造成witness $\vec{a_1},...,\vec{a_m}$的泄露，因此需要引入random vector $\vec{a_0}\leftarrow \mathbb{Z}_q^n$，Prover先commit to $\vec{a_0}$，然后收到challeng $x$后，直接reveal $\vec{a}=\vec{a_0}+\sum_{j=1}^{m}x^j\vec{a_j}$，从而能保证witness不被泄露。
2）在第2步给Verifier传输的 $E_k=\prod_{1\leq i,j\leq m;j=(k-m)+i}\vec{C_i}^{\vec{a_j}}$值，可能也会造成witness $\vec{a_1},...,\vec{a_m}$的泄露。可在此基础上乘以randomn ciphertext $\varepsilon_{pk}(G^{b_k};\tau_k)$【相应地，Prover需在收到challeng $x$前，对 $b_k$进行commit $c_{B_k}=com_{ck}(b_k;s_k)$】，为了仍然保证 $E_m=C$成立，则要求 $b_m=0,s_m=0$。
若考虑 $\rho\neq0$的正常情况，为了仍然保证 $E_m=C$成立，相应的要求 $\tau_m=\rho$。
$\begin{matrix} & \begin{pmatrix} \ \ \ \ \vec{a_0}&\ \ \ \ \vec{a_1} & \cdots &\ \ \ \vec{a_{m-1}} &\ \ \ \ \vec{a_m} \end{pmatrix} & \\ \begin{pmatrix} \vec{C_1}\\ \vec{C_2}\\ \vdots\\ \vec{C_m} \end{pmatrix} & \begin{pmatrix} \vec{C_1}^{\vec{a_0}}& \vec{C_1}^{\vec{a_1}} & \ddots & \vec{C_1}^{\vec{a_{m-1}}} & \vec{C_1}^{\vec{a_m}}\\ \vec{C_2}^{\vec{a_0}} & \vec{C_2}^{\vec{a_1}} & \ddots & \vec{C_2}^{\vec{a_{m-1}}} & \vec{C_2}^{\vec{a_m}}\\ \ddots & \ddots & \ddots & \ddots & \ddots\\ \vec{C_m}^{\vec{a_0}} & \vec{C_m}^{\vec{a_1}} & \ddots & \vec{C_m}^{\vec{a_{m-1}}} & \vec{C_m}^{\vec{a_m}} \end{pmatrix} & \begin{matrix} \\ \varepsilon_{pk}(G^{b_{2m-1}};\tau_{2m-1})E_{2m-1}\\ \vdots\\ \varepsilon_{pk}(G^{b_{m+1}};\tau_{m+1})E_{m+1}\\ \varepsilon_{pk}(1;\rho)E_m \end{matrix} \\ & \begin{matrix} \varepsilon_{pk}(G^{b_0};\tau_0)E_0& \varepsilon_{pk}(G^{b_1};\tau_1)E_1 & \cdots & \varepsilon_{pk}(G^{b_{m-1}};\tau_{m-1})E_{m-1} \end{matrix}& \end{matrix}$
详细算法如下图所示：

3.1 Prover的计算压力

在上述Multi-exponentiation Argument中，Prover需要计算 $E_0,\cdots,E_{2m-1}$，即对于 $k=1,\cdots,2m-1$，有：
$E_k=\prod_{1\leq i,j\leq m;j=(k-m)+i}\vec{C_i}^{\vec{a_j}}=\prod_{i=1,j=1;j=(k-m)+i}^{m,m}\vec{C_i}^{\vec{a_j}}$
对应的计算量有：
1）需有 $m^2$次 $\vec{C_i}^{\vec{a_j}}$次product运算；
2） $\vec{C_i}^{\vec{a_j}}=\prod_{l=1}^{n}C_{il}^{a_{il}}$有 $n$次exponentiation运算in $\mathbb{H}$。
从而 $E_k$有 $mn^2$次exponentiation运算in $\mathbb{H}$。

当 $m$较大时，Prover的计算压力很大，可通过多项式插值（FFT）或Toom-Cook或增加Verifier与Prover交互次数等方式来优化：

• FFT：
  
  
• Toom-Cook：
  
• 增加Verifier与Prover交互次数：基本思路为： $m\times m$矩阵内元素真正有效的仅为对角线上的元素，不需要计算所有 $m^2$个元素，转为将 $m\times m$矩阵切分为小的block矩阵 $\mu \times \mu$（其中 $m=\mu m'$），只需要关注对角线上的block，并使用递归证明对角线block上的内容即可。
  $\begin{pmatrix} \vec{C_1}^{\vec{a_1}} & \ddots & \vec{C_1}^{\vec{a_{m-1}}} & \vec{C_1}^{\vec{a_m}}\\ \vec{C_2}^{\vec{a_1}} & \ddots & \vec{C_2}^{\vec{a_{m-1}}} & \vec{C_2}^{\vec{a_m}}\\ \ddots & \ddots & \ddots & \ddots\\ \vec{C_m}^{\vec{a_1}} & \ddots & \vec{C_m}^{\vec{a_{m-1}}} & \vec{C_m}^{\vec{a_m}} \end{pmatrix}$
  
  

3.2 Prover的计算优化实现

针对3.1中的计算压力，在https://github.com/3for/verifiable-shuffle中分别做了相应的优化实现：

# This parameter determine which version of the program is executed.
# 0 stands for no optimization inside of the code
# 1 uses multi-exponentiation techniques
# 2 uses multi-exponentiation techniques and FFT to find values E_i
# 3 uses multi-exponentiation techniques, extra interaction and Toom-Cook 4 to find values E_i, in this case m =16 or 64\n
3

参考资料：
[1] 2012年论文《Efficient Zero-Knowledge Argument for Correctness of a Shuffle》
[2] PPT 《Efficient Zero-Knowledge Argument for Correctness of a Shuffle》
[3] 博客 向量的Hadamard product VS Inner product
[4] 博客 EIGamal encryption VS Pairing encryption