A (Zero-Knowledge) Vector Commitment with Sum Binding and its Applications学习笔记

1. 引言

Qiang Wang等人2019年发表于Oxford University Press on behalf of the Institute of Mathematics and its Applications 的论文《A (Zero-Knowledge) Vector Commitment with Sum Binding and its Applications》中，主要内容为：

• 在Vector commitment的基础上，提出了增加了sum binding属性的VCS。
• 现有的vector commitment在提供position-binding属性的同时，无法提供隐私保护——即client可能可以通过proofs和commiments获取额外的committed sequence信息。本文提出了zero-knowledge VCS (ZKVCS)—— in which commitments and proofs constructed during the protocol execution leak nothing about the committed sequence。
• 使用(ZK)VCS构建了一个支持 sum 求和运算的(zero-knowledge) verifiable database。

Commitment为密码学中的独立primitive，在zero-knowledge proof，secure computation，e-voting和verifiable secret sharing中均有重要作用。

Commitment具有hiding和binding属性，通常包含2个阶段：

• Committing阶段；
• Opening阶段。

Commitment中通常有2个角色：

• committer：计算commitment $C$；
• client：接收commitment $C$和opening信息。

1.1 commitment发展史

• 1988年，Brassard等人在论文《Minimum disclosure proofs of knowledge》中首次提出了commitment的概念。

• 2004年Gennaro在论文《Multi-trapdoor commitments and their applications to proofs of knowledge secure under concurrent man-in-the-middle attacks》中，2004年MacKenzie等人在论文《On simulation-sound trapdoor commitments》中，2011年Xiaofeng Chen等人在论文《New receipt-free voting scheme using double-trapdoor commitment》中均提到了trapdoor commitment。在trapdoor commitment中，binding属性更灵活，知道trapdoor信息的一方可open the commitment in any possible way，而对于不知道trapdoor信息的一方，仍然具有binding属性。

• 2005年Chase等人在论文《Mercurial commitments with applications to zero-knowledge sets》中，2008年Catalano等人在论文《Zero-knowledge sets with short proofs》中，2010年Benoît Libert和Moti Yung 在论文《Concise Mercurial Vector Commitments and Independent Zero-Knowledge Sets with Short Proofs》中均提到了mercurial commitment。mercurial commitment与trapdoor类似，但是mercurial commitment支持2中open算法：hard open和soft open。在committing阶段，committer可选择是创建hard commitment还是soft commitment。hard commitment支持hard open和soft open，但是open的值只能是当初commit to的值。而soft commitment仅仅支持soft open，soft commitment可open为任意值。mercurial commitment要求没有任何adversary可以区分hard commitment还是soft commitment。（具体可参见博客 Concise Mercurial Vector Commitments and Independent Zero-Knowledge Sets with Short Proofs 学习笔记）

• 2013年， Dario Catalano 和 Dario Fiore 在论文《Vector Commitments and their Applications》中首次提出了vector commitment (VC) 的概念，允许对an ordered sequence of $q$ values $(m_1,\cdots,m_1)$进行commit，同时额外满足position binding属性——即对同一个位置 ，无法open出2个不同的值。（详情参见博客 Vector Commitments and their Applications学习笔记）
  VC的position binding属性可用于check the integrity of outsourced data with fix size。即VC对应的是固定长度的vector。而对于unbounded data呢？

• 2016年，Krupp等人在论文《 Nearly optimal verifiable data streaming》中，将VC扩展为chameleon VC (CVC)，额外增加了chameleon属性——即拥有trapdoor信息的一方可在不改变commitment值的前提下替换各个位置的message值，即可open为任意值。CVC可用于支持unbounded data in verifiable data streaming setting。

但是，以上方法存在以下缺陷：

• Expressiveness：现有的VC scheme仅支持open 位置信息，但是无法满足现实世界的使用需求。如，当已知每个月降雨量的commitment值，现有VC scheme无法支持open全年的降雨量值。因此，除了open位置信息外，也应支持open更多形式的信息。
• Privacy：现有VC scheme的position binding属性仅能保证committer无法对同一位置open出2个不同的值，但是并没有提供隐私保护，a malicious client may learn extra information about the sequence from the proofs and the commitments。

本文提出的VCS (VC with sum binding)，额外支持：

• open the sum of all elements in committed sequence。

本文提出的ZKVCS (zero-knowledge VCS)，无论是open to sum 还是open at position，client都无法获取any information about the committed sequence。hiding property仅能保证malicious client cannot learn any information from the commitments，而ZKVCS可保证malicious client cannot learn any information about the committed squences from the proofs and commitments。

本文的VCS或ZKVCS用于verifiable database时，仍然存在 forward automatic update attack问题，可借助Chen, X.等人2015年论文《New publicly verifiable databases with efficient updates》中的方法进行改进。

1.2 一些定义

• Bilinear pairing:
  

• 多项式分解Polynomial decomposition：
  根据Papamanthou等人2013年论文《Signatures of correct computation》中的Lemma 1， $n$-变量多项式具有如下分解属性：
  
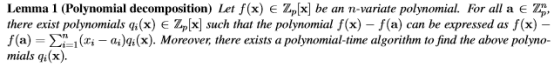
  即polynomial commitment的根本是：
  对于有 $n$个变量（ $\vec{x}=(x_1,\cdots,x_n)$）的多项式 $f(\vec{x})\in\mathbb{Z}_p[\vec{x}]$，对任意取值 $\vec{a}\in\mathbb{Z}_p^n$，存在有效的算法，可找到 $n$个多项式 $Q_i(\vec{x})$，使得 $f(\vec{x})-f(\vec{a})=\sum_{i=1}^{n}(x_i-a_i)\cdot Q_i(\vec{x})$成立。
  

• 相关符号定义：
  

1.3 安全假设

• Bilinear inverse assumption:
  
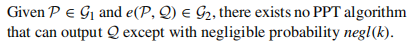
• Bilinear $q$-strong Diffie-Hellman assumption:
  

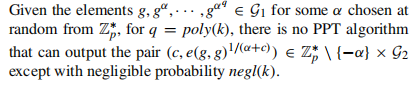
1.4 属性及性能对比

2. VCS基本定义

详情参见博客 Vector Commitments and their Applications学习笔记。
VC由以下6个算法组成：

• VC.KeyGen
• VC.Com
• VC.Open
• VC.Ver
• VC.Update
• VC.ProofUpdate

VCS为了支持sum binding 属性，在VC的基础上，额外增加了2个算法：

• VC.OpenSum
• VC.VerSum

2.1 VCS算法定义

VCS由8个算法（VC.KeyGen,VC.Com,VC.Open,VC.Ver,VC.Update,VC.ProofUpdate,VC.OpenSum,VC.VerSum）组成，各算法定义如下：

• $pp\leftarrow VC.KeyGen(1^k,q)$：key generation算法，输入为security parameter $k$和 $committed vector$的size $q$（ $q=poly(k)$）。输出为public parameters $pp$（which implicitly define the message space $M$）。

• $(C,aux)\leftarrow VC.Com_{pp}(m_1,\cdots,m_q)$：committing算法，由committer运行。输入为a sequence of $q$ messages $m_1,\cdots,m_q\in M$和public parameters $pp$，输出为commitment值 $C$和auxiliary information $aux$。（ $aux$为committer的私有信息。）

• $\Lambda_i\leftarrow VC.Open_{pp}(m_i,i,aux)$：opening算法，由committer运行。输入为public parameters $pp$、位置 $i$、消息 $m_i$以及辅助信息 $aux$，输出为proof $\Lambda_i$（用于证明 $m_i$ is the $i$-th committed message）。

• $\{0,1\}\leftarrow VC.Ver_{pp}(C,m,i,\Lambda_i)$：verification算法，由任意client运行。输入为public parameters $pp$、commitment值 $C$、位置 $i$、opened消息 $m$以及proof $\Lambda_i$。若 $\Lambda_i$为a valid proof that $C$ is a commitment to the sequence $(m_1,\cdots,m_q)$ such that $m=m_i$，则输出为 $1$，否则输出为 $0$。

• $(C',U)\leftarrow VC.Update_{pp}(C,m,m',i)$：update算法，由生成 $C$的原始committer运行，用于update $C$ by changing the $i$-th message $m$ to $m'$。输入为public parameters $pp$、commitment值 $C$、位置 $i$、老的消息 $m$、新消息 $m'$，输出为新的commitment $C'$和update information $U$。

• $(C', \Lambda_j')\leftarrow VC.ProofUpdate_{pp}(C,\Lambda_j,m',U)$：proof update 算法，由任何拥有proof $\Lambda_j$ (for some message at position $j$) client运行。输入为public parameters $pp$、老的commitment值 $C$、proof $\Lambda_j$ (for some message at position $j$)、新的消息 $m'$ (at position $i$)和update information $U$。输出为新的commitment $C'$和新的updated proof $\Lambda_j$ for $m_j$，均对应新的sequence $(m_1,\cdots,m_{i-1},m',m_{i+1},\cdots,m_q)$。

• $\Lambda_{sum}\leftarrow VC.OpenSum_{pp}(sum,aux)$：sum opening算法，由committer运行。输入为public parameters $pp$、sum（ $(m_1,\cdots,m_q)$所有值之和）以及辅助信息 $aux$。输出为proof $\Lambda_{sum}$（用于证明 $sum=\sum_{i=1}^{q}m_i$）。

• $\{0,1\}\leftarrow VC.VerSum_{pp}(C,sum,\Lambda_{sum})$：sum verification算法，可由任意client运行。输入为public parameters $pp$、commitment值 $C$、opened和值 $sum$以及proof $\Lambda_{sum}$。当 $\Lambda_{sum}$ is a valid proof that $C$ is a commitment to the sequence $(m_1,\cdots,m_q)$ such that $sum=\sum_{i=1}^{q}m_i$时，输出为 $1$，否则输出为 $0$。

2.2 VCS correctness定义

即只要算法是honestly executed的，a valid proof should never be rejected。
以下定义为：对vector中的每个位置都依次进行了替换，保证最终的Open和OpenSum均可验证通过。

2.3 VCS position binding 定义

即不允许对同一位置open出2个不同的值。
以下定义为：

• $\mathcal{A}_0$生成任意长度为 $q=poly(k)$的vector。
• 进行 $l+1$次：对vector中的任意位置 $j$（ $\mathcal{A}_1$）进行update，对任意位置 $i$（ $\mathcal{A}_2$）进行Open；
• 根据所获取的 $l+1$组 $(U_a,C_a,\Lambda_a)$信息， $\mathcal{A}_3$选取任意的位置 $i^*$。
• 根据 $i^*$和 $l+1$组 $(U_a,C_a,\Lambda_a)$信息， $\mathcal{A}_4$生成相应的 $(m_{i^*}',\Lambda_{i^*}')$，使得当 $m_{i^*}'\neq m_{i^*}$时对 $\Lambda_{i^*}')$可Ver通过的概率可忽略，即不大于 $negl(k)$。
  
  
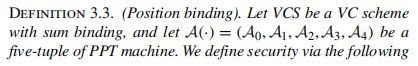
  注意以上新的辅助信息 $aux_a$可由updated information $U_a$和老的辅助信息 $aux_{a-1}$生成。

2.4 VCS sum binding 定义

即不允许open a commitment to two different sums with respect to the committed sequence。
以下定义为：

• $\mathcal{A}_0$生成任意长度为 $q=poly(k)$的vector。
• 进行 $l+1$次：对vector中的任意位置 $j$（ $\mathcal{A}_1$）进行update，对该vector进行OpenSum；
• 根据所获取的 $l+1$组 $(U_a,C_a,\Lambda_{sum_a})$信息， $\mathcal{A}_2$选取其中任意一组vector，生成相应的 $(sum_{l}',\Lambda_{sum_l}')$，使得当 $sum_{l}'\neq sum_l$时对 $\Lambda_{sum_l}')$可VerSum通过的概率可忽略，即不大于 $negl(k)$。
  
  

2.5 concise定义

即 $\Lambda_i$和 $\Lambda_{sum}$与vector的长度 $q$无关。

3. VCS的具体实现

3.1 基于Bilinear pairing的VCS具体实现

• $pp\leftarrow VC.KeyGen(1^k,q)$：key generation算法， $committed vector$的size最大为 $q$，security parameter 为 $k$。选择具有相同order $p\in poly(k)$ 的two groups $\mathcal{G}_1$和 $\mathcal{G}_2$ 满足bilinear map $e:\mathcal{G}_1\times \mathcal{G}_1\rightarrow \mathcal{G}_2$。设置 $\mathcal{G}_1$的generator为 $g$。选择2个随机数 $\alpha,\beta \leftarrow \mathbb{Z}_p$，计算public parameter为：
  $pp=\{g, \{g^{\alpha^i}\}_{i\in [q]} , \{g^{\beta^i}\}_{i\in [q]}, \{g^{\alpha^i\beta^j}\}_{i\in [2q-1]\setminus \{q\},j\in [q]} \}$ 【长度为 $2q^2+1$即为 $\Theta(q^2)$】
  message space为 $M=\mathbb{Z}_p$。

• $(C,aux)\leftarrow VC.Com_{pp}(m_1,\cdots,m_q)$：committing算法，由committer运行。输入为a sequence of $q$ messages $m_1,\cdots,m_q\in M$和public parameters $pp$，计算commitment $C=\prod_{i=1}^{q}(g^{\alpha^i})^{m_i}=\prod_{i=1}^{q}g^{m_i\alpha^i}$，辅助信息 $aux=(m_1,\cdots,m_q)$。
  （ $aux$为committer的私有信息。）

• $\Lambda_i\leftarrow VC.Open_{pp}(m_i,i,aux)$：opening算法，由committer运行。
  基本思路为通过构建2个多项式 $\mathcal{R}(x)$和 $\mathcal{Q}(x,y)$：
  $\mathcal{R}(x)=\sum_{j=1}^{q}m_j\cdot x^j$
  $\mathcal{R}(x)\cdot x^{q-i}y^i=m_i\cdot x^q\cdot y^i+\mathcal{Q}(x,y)$ 公式（1）
  对应的有：
  $\mathcal{Q}(x,y)=(\sum_{j=1,j\neq i}^{q}m_jx^j)\cdot x^{q-i}y^i=\sum_{j=1,j\neq i}^{q}(m_j\cdot x^{q-i+j}y^i)$
  为证明 $m_i$ is the $i$-th committed message，committer可根据public parameters $p$计算对应的proof为 $\Lambda_i=g^{\mathcal{Q}(\alpha,\beta)}$。

• $\{0,1\}\leftarrow VC.Ver_{pp}(C,m_i,i,\Lambda_i)$：verification算法，由任意client运行。输入为public parameters $pp$、commitment值 $C$、位置 $i$、opened消息 $m_i$以及proof $\Lambda_i$。
  直接根据公式（1）验证：
  $e(C,g^{\alpha^{q-i}\beta^i})=e(g^{m_i\cdot \beta^i}, g^{\alpha^q})\cdot e(\Lambda_i,g)$ 公式（2）
  若公式（2）成立，则输出 $1$，否则输出 $0$。

• $(C',U)\leftarrow VC.Update_{pp}(C,m,m',i)$：update算法，由生成 $C$的原始committer运行，用于update $C$ by changing the $i$-th message $m$ to $m'$。
  输出的updated commitment $C'=C\cdot (g^{\alpha^i})^{m'-m}$，updated information $U=(m,m',i)$。

• $(C', \Lambda_j')\leftarrow VC.ProofUpdate_{pp}(C,\Lambda_j,m',U)$：proof update 算法，由任何拥有proof $\Lambda_j$ (for some message at position $j$) client运行。输入为public parameters $pp$、老的commitment值 $C$、proof $\Lambda_j$ (for some message at position $j$)、新的消息 $m'$ (at position $i$)和update information $U$。输出为新的commitment $C'$和新的updated proof $\Lambda_j$ for $m_j$，均对应新的sequence $(m_1,\cdots,m_{i-1},m',m_{i+1},\cdots,m_q)$。根据 $i$与 $j$的关系分为如下2中情况：
  1）当 $j\neq i$时，updated commitment $C'=C\cdot (g^{\alpha^i})^{m'-m}$，updated proof为 $\Lambda_j'=\Lambda_j\cdot g^{(m'-m)\cdot \alpha^{q-j+i}\beta^j}$。
  2）当 $j=i$时，updated commitment $C'=C\cdot (g^{\alpha^i})^{m'-m}$，updated proof仍然为 $\Lambda_j$保持不变。

• $\Lambda_{sum}\leftarrow VC.OpenSum_{pp}(sum,aux)$：sum opening算法，由committer运行。输入为public parameters $pp$、sum（ $(m_1,\cdots,m_q)$所有值之和）以及辅助信息 $aux$。输出为proof $\Lambda_{sum}$（用于证明 $sum=\sum_{i=1}^{q}m_i$）。
  基本思路为：
  构建多项式 $\mathcal{R}(x)=\sum_{j=1}^{q}m_jx^j$，当取 $x=1$时，有 $\mathcal{R}(1)=\sum_{j=1}^{q}m_j=sum$。同时，利用polynomial decomposition有：
  $\mathcal{R}(x)-\mathcal{R}(1)=(x-1)\cdot \mathcal{Q}(x)$
  计算OpenSum proof 为 $\Lambda_{sum}=g^{\mathcal{Q}(\alpha)}$。

• $\{0,1\}\leftarrow VC.VerSum_{pp}(C,sum,\Lambda_{sum})$：sum verification算法，可由任意client运行。输入为public parameters $pp$、commitment值 $C$、opened和值 $sum$以及proof $\Lambda_{sum}$。
  验证：
  $e(C/g^{sum},g)=e(\Lambda_{sum},g^{\alpha-1})=e(\Lambda_{sum},g^{\alpha}/g)$
  是否成立，若成立，则输出 $1$，否则输出 $0$。

3.2 基于Bilinear pairing VCS的security analysis

分别呼应第2节中的correctness定义、position binding定义、sum binding定义和concise定义有correctness security、position binding security、sum binding security和concise security。

• correctness security：
  由3.1节内容很容易验证correctness。

• position binding security：
  采用归谬法来证明。
  假设adversary $\mathcal{A}$可构建算法 $\mathcal{B}$，使得2.3节中的position binding的概率不可忽略，从而使position binding security不成立。
  即存在 $m_{i^*}'\neq m_{i^*}$，使得 $VC.Ver_{pp}(C_l, m_{i^*}',i^*,\Lambda_{i^*}')=1$成立。
  也就是说以下两个等式同时成立：
  $e(C,g^{\alpha^{q-i^*}\beta^{i^*}})=e(g^{m_{i^*}'\cdot \beta^i}, g^{\alpha^q})\cdot e(\Lambda_{i^*}',g)$
  $e(C,g^{\alpha^{q-i^*}\beta^{i^*}})=e(g^{m_{i^*}\cdot \beta^i}, g^{\alpha^q})\cdot e(\Lambda_{i^*},g)$
  两个公式结合有：
  $e(g^{m_{i^*}'\cdot \beta^i}, g^{\alpha^q})\cdot e(\Lambda_{i^*}',g)= e(g^{m_{i^*}\cdot \beta^i}, g^{\alpha^q})\cdot e(\Lambda_{i^*},g)$
  对应有：【假设 $c= m_{i^*}'- m_{i^*}$】
  $e(\Lambda_{i^*}',g)= e(g^{m_{i^*}\cdot \beta^i}, g^{\alpha^q})\cdot e(\Lambda_{i^*},g)/ e(g^{m_{i^*}'\cdot \beta^i}, g^{\alpha^q})= e(g^{(m_{i^*}- m_{i^*}')\cdot \alpha^q\beta^i}, g)\cdot e(\Lambda_{i^*},g)= e(g^{(m_{i^*}- m_{i^*}')\cdot \alpha^q\beta^i}\cdot \Lambda_{i^*}, g)= e(g^{c\cdot \alpha^q\beta^i}\cdot \Lambda_{i^*}, g)$
  也就是说，已知 $g$和 $e(\Lambda_{i^*}',g)$值，adversary $\mathcal{A}$可找到相应的 $\Lambda_{i^*}'$值。而这与bilinear inverse assumption冲突。
  所以在bilinear inverse assumption条件下，position binding security可保证。

• sum binding security
  仍然采用归谬法来证明。
  假设adversary $\mathcal{A}$可构建算法 $\mathcal{B}$，使得2.4节中的sum binding的概率不可忽略，从而使sum binding security不成立。
  即存在 $sum_{l}'\neq sum_l$，使得 $VC.VerSum_{pp}(C_l,sum_l',\Lambda_{sum_l}')=1$成立。
  也就是说以下两个等式同时成立：
  $e(C_l/g^{sum_l'},g)=e(\Lambda_{sum_l}',g^{\alpha-1})$
  $e(C_l/g^{sum_l},g)=e(\Lambda_{sum_l},g^{\alpha-1})$
  两个公式结合有：【 $\because (\Lambda_{sum_l}=g^{\mathcal{Q}_l(\alpha)}，(\Lambda_{sum_l}'=g^{\mathcal{Q}_l'(\alpha)}$】
  $e(g^{\mathcal{Q}_l'(\alpha)},g^{\alpha-1})\cdot e(g^{sum_l'},g)= e(g^{\mathcal{Q}_l(\alpha)},g^{\alpha-1})\cdot e(g^{sum_l},g)$
  对应有：
  $e(g,g)^{sum_l'-sum_l}=e(g,g)^{(\mathcal{Q}_l(\alpha)-\mathcal{Q}_l'(\alpha))\cdot (\alpha-1)}$
  由于 $sum_l'\neq sum_l$，于是有：
  $e(g,g)^{1/{\alpha-1}}=e(g,g)^{\frac{\mathcal{Q}_l(\alpha)-\mathcal{Q}_l'(\alpha)}{sum_l'-sum_l}}$
  也就是说，已知 $g,g^{\alpha},\cdots,g^{\alpha^q}\in \mathcal{G}_1$，adversary $\mathcal{A}$可找到 $c=-1$并计算出 $e(g,g)^{1/(\alpha+c)}$的值。而这与bilinear $q$-strong Diffie-Hellman assumption冲突。
  所以在bilinear $q$-strong Diffie-Hellman assumption条件下，sum binding security可保证。

• concise security
  观察3.1节的具体实现VC.Com的输出 $C$、VC.Open的输出 $\Lambda_i$和VC.OpenSum的输出 $\Lambda_{sum}$均为one single element in $\mathcal{G}_1$。
  所以满足concise定义。

4. ZKVCS

ZKVCS，即zero-knowledge vector commitments with sum binding。
ZKVCS在VCS的基础上，额外增加了zero-knowledge属性。
VCS的position binding和sum binding仅可保证针对同一commitment，不能对同一position open出2个不同的值，不能对同一vector open出2个sum值。并没有考虑到隐私的问题，即 What does the client may learn about the committed sequence from the commitments and proofs。
ZKVCS可保证a malicious client gets no information about the committed sequence beyond what is opened during the protocol execution。

受限于文章篇幅，主要针对ZKVCS的zero-knowledge属性，通过real/ideal experiment来定义。

4.1 ZKVCS的zero knowledge定义

直觉上来说，a ZKVCS scheme achieves zero-knowledge if there exists a simulator with no knowledge of the sequence or the updates that occur such that arbitrary adversarial client cannot distinguish whether he is interacting with the algorithms of the scheme or with the simulator。
zero-knowledge主要体现在open阶段，分别对应Open和OpenSum算法，对应有zero-knowledge opening和zero-knowledge sum opening。

4.1.1 Zero-knowledge opening定义

存在的参与方有：challenger $\mathcal{C}$，adversary $\mathcal{A}$和simulator $\mathcal{S}$。

Zero-knowledge opening定义是指：adversary $\mathcal{A}$无法区分其是在跟challenger $\mathcal{C}$进行Open交互还是在跟simulator $\mathcal{S}$进行Open交互。其中simulator $\mathcal{S}$并不知道adversary $\mathcal{A}$所选择的vector信息。

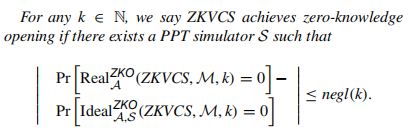
Real流程为：

• challenger $\mathcal{C}$生成public parameter $pp$，并将 $pp$发送给adversary $\mathcal{A}$。
• adversary $\mathcal{A}$选择任意的vector $M_0=(m_1,\cdots,m_q)$，并将 $M_0$ 发送给challenger $\mathcal{C}$。
• challenger $\mathcal{C}$运行 $(C_0,aux_0)\leftarrow VC.Com_{pp}(M_0)$，并将commitment $C_0$发送给adversary $\mathcal{A}$。
• 运行 $l+1$次（ $a=0;a++;a<=l$）（其中 $l=poly(k)$）： adversary $\mathcal{A}$选择任意的 $(i,j,m_j'),i\in[q],j\in[q]$发送给 challenger $\mathcal{C}$，其中 $i$代表要open的位置， $j$表示要update的位置；challenger $\mathcal{C}$ Open 位置 $i$ proof $\Lambda_a$发送给adversary $\mathcal{A}$，update位置 $j$为 $m_j'$将相应的 $C_{a+1}$发送给adversary $\mathcal{A}$。
• adversary $\mathcal{A}$ 验证 $\Lambda_a$是否正确，输出bit $b$。
  

Ideal流程为：

• simulator $\mathcal{S}$生成public parameter $pp$，并将 $pp$发送给adversary $\mathcal{A}$。
• adversary $\mathcal{A}$选择任意的vector $M_0=(m_1,\cdots,m_q)$。【注意此时 $M_0$不发送给simulator $\mathcal{S}$】
• simulator $\mathcal{S}$ (without seeing $M_0$) 运行 $C_0\leftarrow \mathcal{S}_1(pp)$，并将 $C_0$发送给adversary $\mathcal{A}$。
• 运行 $l+1$次（ $a=0;a++;a<=l$）（其中 $l=poly(k)$）： adversary $\mathcal{A}$选择任意的 $(i,j,m_j'),i\in[q],j\in[q]$发送给 simulator $\mathcal{S}$，其中 $i$代表要open的位置， $j$表示要update的位置；simulator $\mathcal{S}$ Open 位置 $i$ proof $\Lambda_a$发送给adversary $\mathcal{A}$，update位置 $j$为 $m_j'$将相应的 $C_{a+1}$发送给adversary $\mathcal{A}$。
• adversary $\mathcal{A}$ 验证 $\Lambda_a$是否正确，输出bit $b$。
  

4.1.2 Zero-knowledge sum opening定义

存在的参与方有：challenger $\mathcal{C}$，adversary $\mathcal{A}$和simulator $\mathcal{S}$。

Zero-knowledge sum opening定义是指：adversary $\mathcal{A}$无法区分其是在跟challenger $\mathcal{C}$进行OpenSum交互还是在跟simulator $\mathcal{S}$进行OpenSum交互。其中simulator $\mathcal{S}$并不知道adversary $\mathcal{A}$所选择的vector信息。

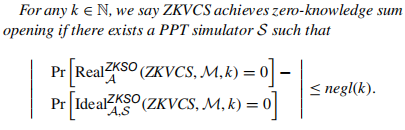
Real流程为：

• challenger $\mathcal{C}$生成public parameter $pp$，并将 $pp$发送给adversary $\mathcal{A}$。
• adversary $\mathcal{A}$选择任意的vector $M_0=(m_1,\cdots,m_q)$，并将 $M_0$ 发送给challenger $\mathcal{C}$。
• challenger $\mathcal{C}$运行 $(C_0,aux_0)\leftarrow VC.Com_{pp}(M_0)$，并将commitment $C_0$发送给adversary $\mathcal{A}$。
• 运行 $l+1$次（ $a=0;a++;a<=l$）（其中 $l=poly(k)$）： adversary $\mathcal{A}$选择任意的 $(i,j,m_j'),i\in[q],j\in[q]$发送给 challenger $\mathcal{C}$，其中 $i$代表要open的位置， $j$表示要update的位置；challenger $\mathcal{C}$ OpenSum 位置 $i$ proof $\Lambda_{sum_a}$发送给adversary $\mathcal{A}$，update位置 $j$为 $m_j'$将相应的 $C_{a+1}$发送给adversary $\mathcal{A}$。
• adversary $\mathcal{A}$ 验证 $\Lambda_{sum_a}$是否正确，输出bit $b$。

Ideal流程为：

• simulator $\mathcal{S}$生成public parameter $pp$，并将 $pp$发送给adversary $\mathcal{A}$。
• adversary $\mathcal{A}$选择任意的vector $M_0=(m_1,\cdots,m_q)$。【注意此时 $M_0$不发送给simulator $\mathcal{S}$】
• simulator $\mathcal{S}$ (without seeing $M_0$) 运行 $C_0\leftarrow \mathcal{S}_1(pp)$，并将 $C_0$发送给adversary $\mathcal{A}$。
• 运行 $l+1$次（ $a=0;a++;a<=l$）（其中 $l=poly(k)$）： adversary $\mathcal{A}$选择任意的 $(i,j,m_j'),i\in[q],j\in[q]$发送给 simulator $\mathcal{S}$，其中 $i$代表要open的位置， $j$表示要update的位置；simulator $\mathcal{S}$ OpenSum 位置 $i$ proof $\Lambda_{sum_a}$发送给adversary $\mathcal{A}$，update位置 $j$为 $m_j'$将相应的 $C_{a+1}$发送给adversary $\mathcal{A}$。
• adversary $\mathcal{A}$ 验证 $\Lambda_{sum_a}$是否正确，输出bit $b$。

4.2 基于bilinear map的ZKVCS具体实现

• $pp\leftarrow VC.KeyGen(1^k,q)$：key generation算法， $committed vector$的size最大为 $q$，security parameter 为 $k$。选择具有相同order $p\in poly(k)$ 的two groups $\mathcal{G}_1$和 $\mathcal{G}_2$ 满足bilinear map $e:\mathcal{G}_1\times \mathcal{G}_1\rightarrow \mathcal{G}_2$。设置 $\mathcal{G}_1$的generator为 $g$。选择2个随机数 $\alpha,\beta,\gamma \leftarrow \mathbb{Z}_p$，计算public parameter为：
  $pp=\{g,g^{\gamma}, \{g^{\alpha^i}\}_{i\in [q]} , \{g^{\beta^i}\}_{i\in [q]}, \{g^{\alpha^i\beta^j}\}_{i\in [2q-1]\setminus \{q\},j\in [q]},\{g^{\alpha^i\beta^j\gamma}\}_{i\in [q],j\in [q],i+j=q} \}$ 【长度为 $2q^2+q+2$即为 $\Theta(q^2)$】
  message space为 $M=\mathbb{Z}_p$。
  【将 $\alpha,\beta,\gamma$看成trapdoor信息的话，可具有chameleon属性。】

• $(C,aux)\leftarrow VC.Com_{pp}(m_1,\cdots,m_q)$：committing算法，由committer运行。输入为a sequence of $q$ messages $m_1,\cdots,m_q\in M$和public parameters $pp$。
  committer选择随机数 $r\leftarrow \mathbb{Z}_p$，构建多项式 $\mathcal{R}(x,z)=\sum_{j=1}^{q}m_j\cdot x^j+r\cdot z$
  计算commitment $C=g^{\mathcal{R}(\alpha,\gamma)}=\prod_{j=1}^{q}(g^{\alpha^j})^{m_j}\cdot (g^{\gamma })^r=\prod_{j=1}^{q}g^{m_j\alpha^j}\cdot g^{\gamma r}$，辅助信息 $aux=(m_1,\cdots,m_q,r)$。
  （ $aux$为committer的私有信息。）

• $\Lambda_i\leftarrow VC.Open_{pp}(m_i,i,aux)$：opening算法，由committer运行。
  基本思路为通过构建2个多项式 $\mathcal{R}(x,z)$和 $\mathcal{Q}(x,y,z)$：
  $\mathcal{R}(x,z)=\sum_{j=1}^{q}m_j\cdot x^j+r\cdot z$
  $\mathcal{R}(x,z)\cdot x^{q-i}y^i=m_i\cdot x^q\cdot y^i+\mathcal{Q}(x,y,z)$ 公式（11）
  对应的有：
  $\mathcal{Q}(x,y,z)=(\sum_{j=1,j\neq i}^{q}m_jx^j+r\cdot z)\cdot x^{q-i}y^i=\sum_{j=1,j\neq i}^{q}(m_j\cdot x^{q-i+j}y^i)+r\cdot x^{q-i}y^iz$
  为证明 $m_i$ is the $i$-th committed message，committer可根据public parameters $p$计算对应的proof为 $\Lambda_i=g^{\mathcal{Q}(\alpha,\beta,\gamma)}$。

• $\{0,1\}\leftarrow VC.Ver_{pp}(C,m_i,i,\Lambda_i)$：verification算法，由任意client运行。输入为public parameters $pp$、commitment值 $C$、位置 $i$、opened消息 $m_i$以及proof $\Lambda_i$。
  直接根据公式（11）验证：
  $e(C,g^{\alpha^{q-i}\beta^i})=e(g^{m_i\cdot \beta^i}, g^{\alpha^q})\cdot e(\Lambda_i,g)$ 公式（12）
  若公式（12）成立，则输出 $1$，否则输出 $0$。

• $(C',U)\leftarrow VC.Update_{pp}(C,m,m',i)$：update算法，由生成 $C$的原始committer运行，用于update $C$ by changing the $i$-th message $m$ to $m'$。
  committer选择随机数 $r'\leftarrow \mathbb{Z}_p$，
  输出的updated commitment $C'=C\cdot (g^{\alpha^i})^{m'-m}\cdot g^{r'\cdot \gamma}$，updated information $U=(m,m',i,r')$。

• $(C', \Lambda_j')\leftarrow VC.ProofUpdate_{pp}(C,\Lambda_j,m',U)$：proof update 算法，由任何拥有proof $\Lambda_j$ (for some message at position $j$) client运行。输入为public parameters $pp$、老的commitment值 $C$、proof $\Lambda_j$ (for some message at position $j$)、新的消息 $m'$ (at position $i$)和update information $U$。输出为新的commitment $C'$和新的updated proof $\Lambda_j$ for $m_j$，均对应新的sequence $(m_1,\cdots,m_{i-1},m',m_{i+1},\cdots,m_q)$。根据 $i$与 $j$的关系分为如下2中情况：
  1）当 $j\neq i$时，updated commitment $C'=C\cdot (g^{\alpha^i})^{m'-m}\cdot g^{r'\cdot \gamma}$，updated proof为 $\Lambda_j'=\Lambda_j\cdot g^{(m'-m)\cdot \alpha^{q-j+i}\beta^j}\cdot g^{r'\cdot \alpha^{q-j}\beta^j\gamma}$。
  2）当 $j=i$时，updated commitment $C'=C\cdot (g^{\alpha^i})^{m'-m}\cdot g^{r'\cdot \gamma}$，updated proof为 $\Lambda_j'=\Lambda_j\cdot g^{r'\cdot \alpha^{q-j}\beta^j\gamma}$。

• $\Lambda_{sum}\leftarrow VC.OpenSum_{pp}(sum,aux)$：sum opening算法，由committer运行。输入为public parameters $pp$、sum（ $(m_1,\cdots,m_q)$所有值之和）以及辅助信息 $aux$。输出为proof $\Lambda_{sum}$（用于证明 $sum=\sum_{i=1}^{q}m_i$）。
  基本思路为：
  构建多项式 $\mathcal{R}(x,z)=\sum_{j=1}^{q}m_j\cdot x^j+r\cdot z$，当取 $x=1,z=0$时，有 $\mathcal{R}(1,0)=\sum_{j=1}^{q}m_j=sum$。同时，利用polynomial decomposition有：
  $\mathcal{R}(x,z)-\mathcal{R}(1,0)=(x-1)\cdot \mathcal{Q}_1(x,z)+z\cdot \mathcal{Q}_2(x,z)$
  committer选择随机数 $\delta\leftarrow \mathbb{Z}_p$，有：
  $\mathcal{R}(x,z)-\mathcal{R}(1,0)=[(x-1)\cdot \mathcal{Q}_1(x,z)+\delta\cdot (x-1)z]+[z\cdot \mathcal{Q}_2(x,z)-\delta\cdot (x-1)z]=(x-1)\cdot( \mathcal{Q}_1(x,z)+\delta z)+z\cdot (\mathcal{Q}_2(x,z)-\delta (x-1))=(x-1)\cdot\Lambda_{sum}^1+z\cdot \Lambda_{sum}^2$
  计算OpenSum proof 为 $\Lambda_{sum}=(\Lambda_{sum}^1,\Lambda_{sum}^2)=(g^{\mathcal{Q}_1(\alpha,\gamma)+\delta\gamma},g^{\mathcal{Q}_2(\alpha,\gamma)-\delta(\alpha-1)})$。

• $\{0,1\}\leftarrow VC.VerSum_{pp}(C,sum,\Lambda_{sum})$：sum verification算法，可由任意client运行。输入为public parameters $pp$、commitment值 $C$、opened和值 $sum$以及proof $\Lambda_{sum}$。
  验证：
  $e(C/g^{sum},g)=e(\Lambda_{sum}^1,g^{\alpha-1})\cdot e(\Lambda_{sum}^2,g^{\gamma})$
  是否成立，若成立，则输出 $1$，否则输出 $0$。

4.3 ZKVCS security analysis

• position binding security
  ZKVCS的Ver与VCS的Ver所验证的公式类似，均为 $e(C,g^{\alpha^{q-i}\beta^i})=e(g^{m_i\cdot \beta^i}, g^{\alpha^q})\cdot e(\Lambda_i,g)$ 。可采用类似3.2节position binding security的方式归谬法证明。
  所以在bilinear inverse assumption条件下，ZKVCS的position binding security可保证。

• sum binding security
  采用归谬法，证明思路如下：
  
  
  因此，在bilinear $q$-strong Diffie-Hellman assumption条件下，ZKVCS的sum binding security可保证。

• concise security
  ZKVCS的VC.Com的输出 $C$、VC.Open的输出 $\Lambda_i$均为one single element in $\mathcal{G}_1$。而VC.OpenSum的输出 $\Lambda_{sum}$均为2个 elements in $\mathcal{G}_2$。都与vector size $q$无关。满足concise定义要求。

• zero-knowledge opening security
  证明如下：（根本思路是simulator $\mathcal{S}$知道trapdoor $\alpha,\beta,\gamma$信息，可伪造 $Q(x,y,z)=\mathcal{R}(x,z)\cdot x^{q-i}y^i-m_i\cdot x^q\cdot y^i$，使得 $\mathcal{R}(x,z)\cdot x^{q-i}y^i=m_i\cdot x^q\cdot y^i+Q(x,y,z)$恒成立。）
  

• zero-knowledge sum opening security
  证明如下：（根本思路是simulator $\mathcal{S}$知道trapdoor $\alpha,\beta,\gamma$信息，可伪造 $\Lambda_{sum}^1=\frac{\mathcal{R}(x,z)-\mathcal{R}(1,0)-\delta}{x-1}, \Lambda_{sum}^2=\frac{\delta}{z}$ 使得 $\mathcal{R}(x,z)-\mathcal{R}(1,0)=(x-1)\cdot\Lambda_{sum}^1+z\cdot \Lambda_{sum}^2$恒成立）