将一个整数分解为2的幂次的拆分数

题目：https://acm.ecnu.edu.cn/problem/3034/

一、开始思考

找了一波规律，然后发现了如果n是奇数，那么f(n)=f(n-1)

然后去搜索了一下拆分数，发现一个讲述了求正整数的所有拆分数的，和这个有些类似。引入一个拆分的组合中的最大数m，由此可以分为最大数包括这个m的组合与最大数不包括m的组合。f(n,m)表示和为n，最大数为m的拆分数。

f(n,m) = f(n,m-1) + f(n-m,m)

f(n,m-1)表示最大数肯定不是m的组合数； f(n-m,m)表示最大数肯定是m的组合数。

类似的，对于本题可以得到推导式：

f(n,m) = f(n,m/2) + f(n-m,m)

对于n == m时：

f(n,m) = f(n,m/2) + 1

所有的情况有：

if(n == 1 或者 m == 1)

　　f(n,m) = 1

if(n < m)

　　f(n,m) = f(n,n)

if(n == m)

　　f(n,m) = f(n,m/2) + 1

else:

　　f(n,m) = f(n,m/2) + f(n-m,m)

写代码时，注意这个m始终要保证是2的幂次数。

版本1：

/**
    求拆分数的递归实现
*/
#include<bits/stdc++.h>
using namespace std;
//求得不大于x的最大的，可以由2的幂次得到的数
int getV(int x){
    int t,cnt;
    t = x;
    cnt = 0;
    while(t!=0){
        t>>=1;
        cnt++;
    }
    cnt--;
    return (1<<cnt);
}
//核心递归计算
int f_cal(int m,int n){
    if(m == 1|| n == 1)
        return 1;
    if(m < n){
        return f_cal(m,getV(m));
    }else if(n == m){
        return 1 + f_cal(m,getV(n/2));
    }
    //肯定有 n  和肯定没有n的组成
    return f_cal(m,getV(n/2)) + f_cal(m-n,n);
}
int main(){
    int T;
    //cal();
    cin >> T;
    int n,m;
    for(int i = 0;i < T;i++){
        cin >> m;
        n = getV(m);
        //n = getVM(m);
        cout << "case #" << i << ":" << endl;
        cout << f_cal(m,n) << endl;
        //cout << mm[m][n] << endl;
    }
    return 0;
}

会超时的。

二、优化

记忆化处理一下：

版本2：

/**
    求拆分数的递归实现
*/
#include<bits/stdc++.h>
using namespace std;
unsigned long long mm[1000001][21];

const int MN = 1000000000;
//求得幂次
int getVM(int x){
    int t,cnt;
    t = x;
    cnt = 0;
    while(t!=0){
        t>>=1;
        cnt++;
    }
    cnt--;
    return cnt;
}
//循环计算
void cal(){
    for(int i = 0;i < 1000001;i++){
        mm[i][0] = 1;
    }
    for(int i = 0;i < 21;i++){
        mm[1][i] = 1;
    }
    for(int i = 2;i < 1000001;i++){
        for(int j = 1;j < 21;j++){
            if(i < (1 << j)){
                mm[i][j] = mm[i][getVM(i)];
            }else if(i == (1 << j)){
                mm[i][j] = (mm[i][j-1] % MN + 1) % MN;
            }else{
                mm[i][j] = (mm[i][j-1] % MN + mm[i - (1<<j)][j] % MN) % MN;
            }
        }
    }
}

int main(){
    int T;
    cal();
    cin >> T;
    int n,m;
    for(int i = 0;i < T;i++){
        cin >> m;

        n = getVM(m);
        cout << "case #" << i << ":" << endl;
        //cout << f_cal(m,n) << endl;
        cout << mm[m][n] % MN << endl;
    }
    return 0;
}

这个代码已经AC了。看完代码会发现，为什么我会模1000000000？？？我在分析错误样例时发现，有的正确答案正好是我的答案的后半部分！？？！？？！我突然有了大胆的假设》《

查了一下这个题，讨论区都是，有模？。。竟然是真的

加上这个神奇的模

顺利AC

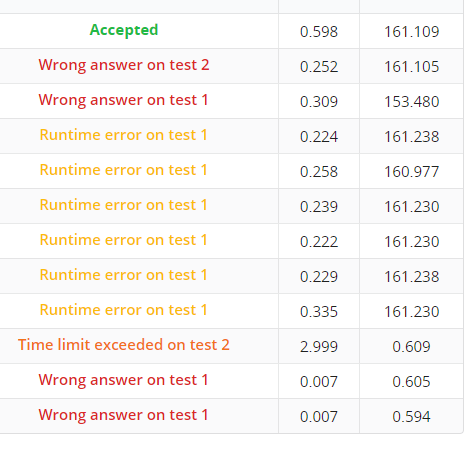
啥？为什么re了这么多次？因为，我在之前递归版本上直接记忆化，它就RE，不知道为啥。我不信这个邪，多交了几次，结果评测机赢了。

三、简化代码

在讨论区发现，有一个一维数组就解决了的！学习了一下。它的分配是根据组合中有没有1，重点就在于对这个的证明了。很完美。链接在下--

　　【转】原文链接：https://blog.csdn.net/zhang20072844/java/article/details/17033931

改进效果：

版本3：

/**
    求拆分数的递归实现
*/
#include<bits/stdc++.h>
using namespace std;
unsigned long long mm[1000001];

const int MN = 1000000000;

//循环计算
void cal(){
    mm[0] = 1;
    for(int i = 1;i < 1000001;i++){
        if(i%2){
            mm[i] = mm[i-1];
        }else{
            //分为含有1和不含有1的组合
            mm[i] = (mm[i-1] + mm[i/2])%MN;
        }
    }
}

int main(){
    int T;
    cal();
    cin >> T;
    int n,m;
    for(int i = 0;i < T;i++){
        cin >> m;
        cout << "case #" << i << ":" << endl;
        //cout << f_cal(m,n) << endl;
        cout << mm[m] % MN << endl;
    }
    return 0;
}

将一个整数分解为2的幂次的拆分数

猜你喜欢