1. 时间复杂度

1.1 时间复杂度的种类 Big O Notation

O(1)-Constant Complexity 常数复杂度
O(log n)- Logarithmic Complexity 对数复杂度
O(n)-Linear Complexity 线性时间复杂度
O(n^2)-N Square Complexity 平方
O(n^3)-N cubic Complexity 立方
O(2^n)-Exponential Growth 指数
O(n!)-Factorial 阶乘

[ˌekspəˈnenʃl], [ˌlɒɡəˈrɪðmɪk] , [fækˈtɔːriəl] , [kəmˈpleksəti]
注意：

O 是复杂度函数 O(？(n)) 代表是 函数调用次数和n的数学关系
只关注与 n的数学关系而不关注于n的系数，因此O(1) 代表可能运算了1次，2次，或者x次但都是常数. O(n)可能运算了n次，2n次或者xn次, 我们并不关注.
在程序中我们只关注 最高复杂度的运算
复杂度是对一个函数而言的, 因此我们关注当给定一个特定的n时(n可能为二叉树节点数目或类似的) 该程序第调用次数与n有着怎样的数学关系(而不是执行多少次, 我们不关注系数)
时间复杂度的高低从到下依次递增(当n较大时)

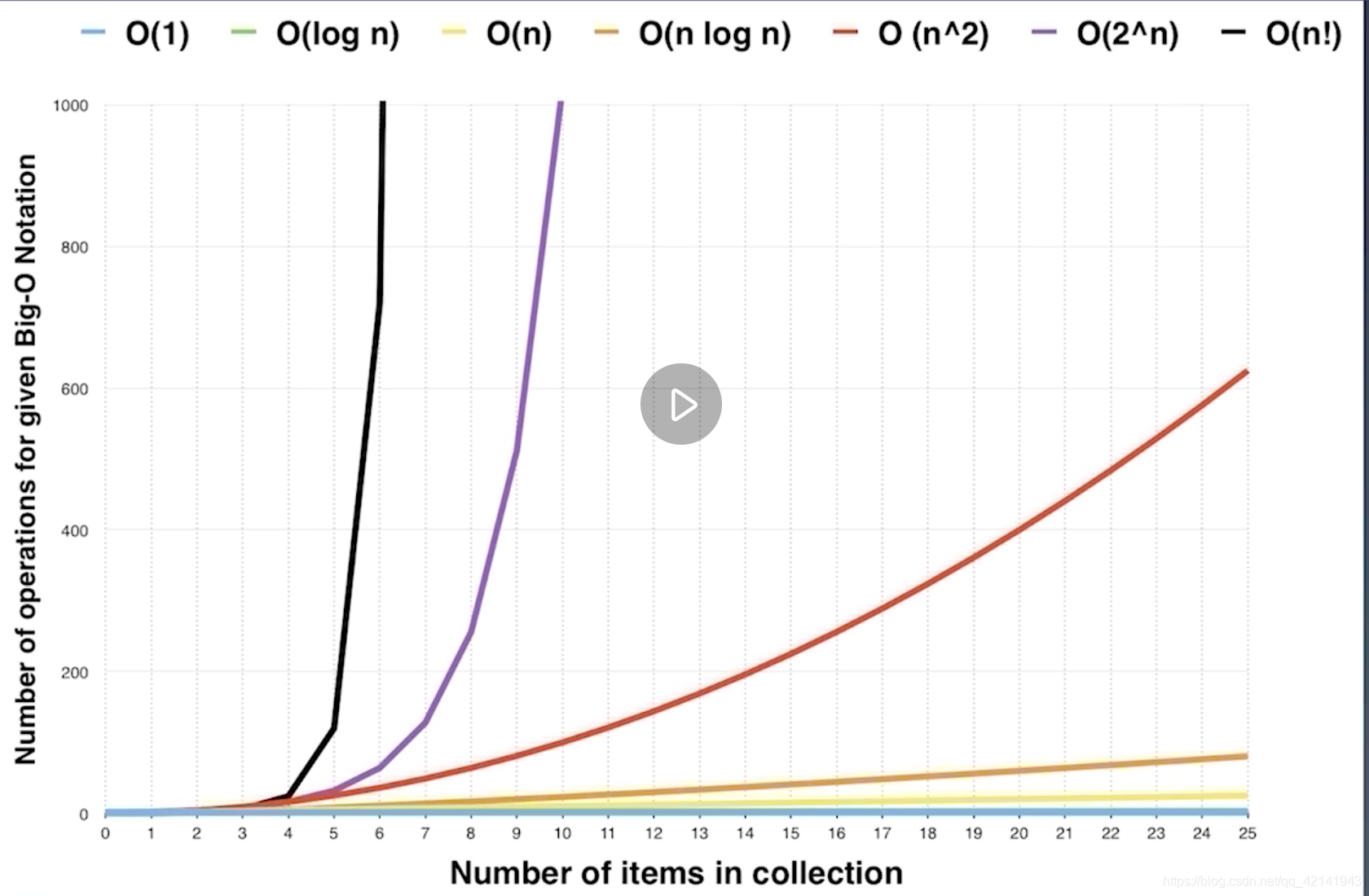
1.2 简单的时间复杂度分析

1.21. 常数复杂度

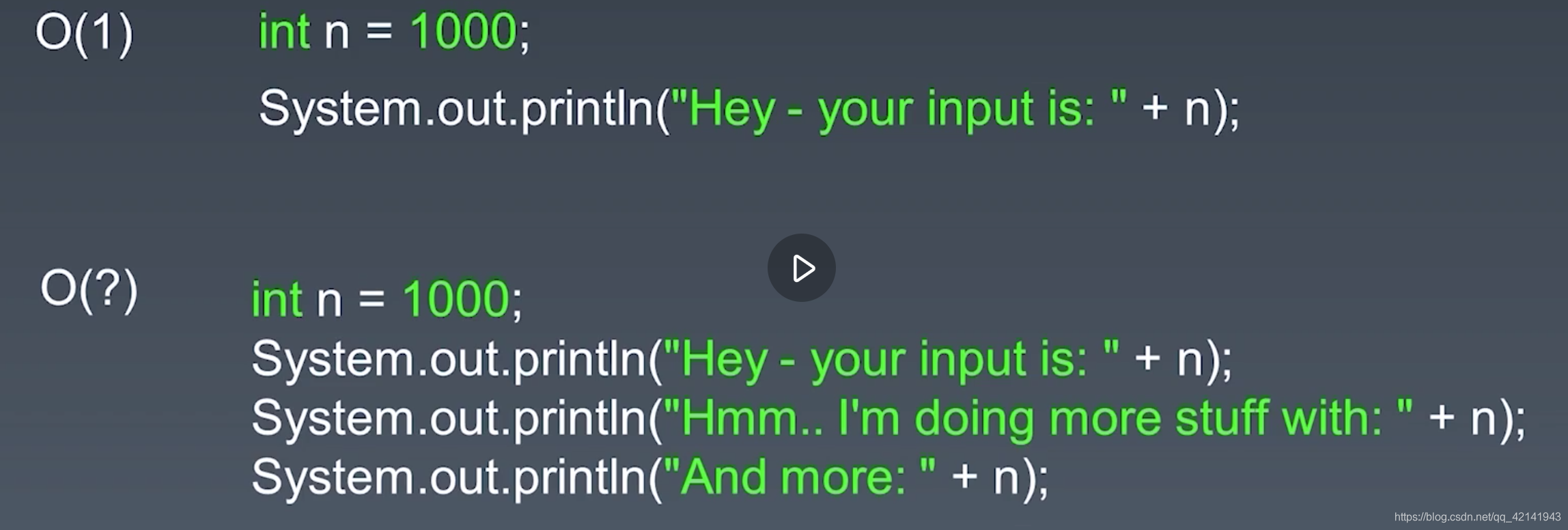
在这里插入图片描述

若把System.out.println当做函数的话，我们的目的是去判断该函数和n的关系
很明显和n几乎没有关系第一段运行1次的二段运行三次. 因此第一段第二段代码的时间复杂度均为-常数时间复杂度即O(1)(我们关注的是数学关系而不是精确数目) 因为函数和n之间的关系为常数关系, 即n的数目不会影响函数调用次数

1.22 Linear Complexity 和 Square Complexity

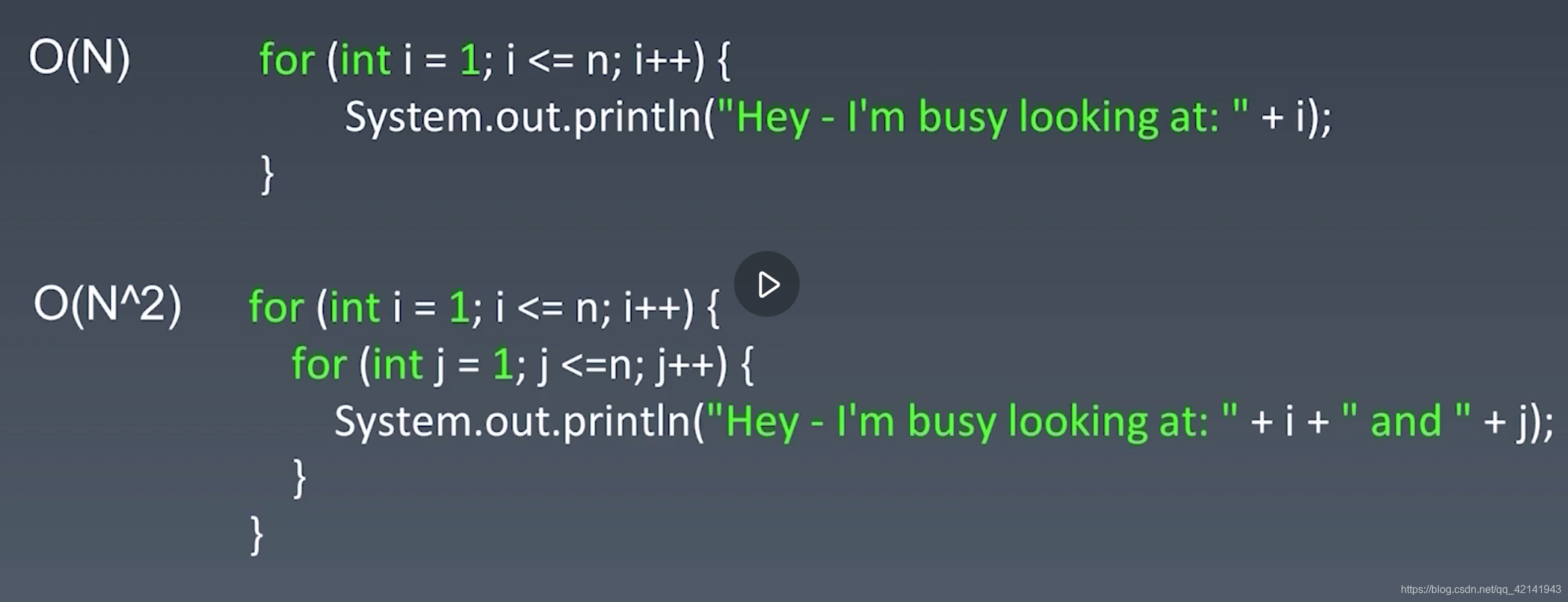
在这里插入图片描述

第一段代码很显然函数于n的关系为线性的，因为n为多少次for循环就执行了多少次，所以这里函数与n的关系为线性的复杂度为O(n)
第二段代码函数执行了n*n次，第一个n是外循环，第二个n是内循环，因此函数调用次数与n的关系为n^2因此复杂度为O( n ^2)
如果第二个函数中两个function是并列的那么函数的调用关系与n的关系为调用数为2n，因此时间复杂度为O(n)也就是线性复杂度(不关心系数)
如果是ijk的三层嵌套的话自然而然就变成了O(n^3).

1.23 Logarithmic Complexity 和 Exponential Growth

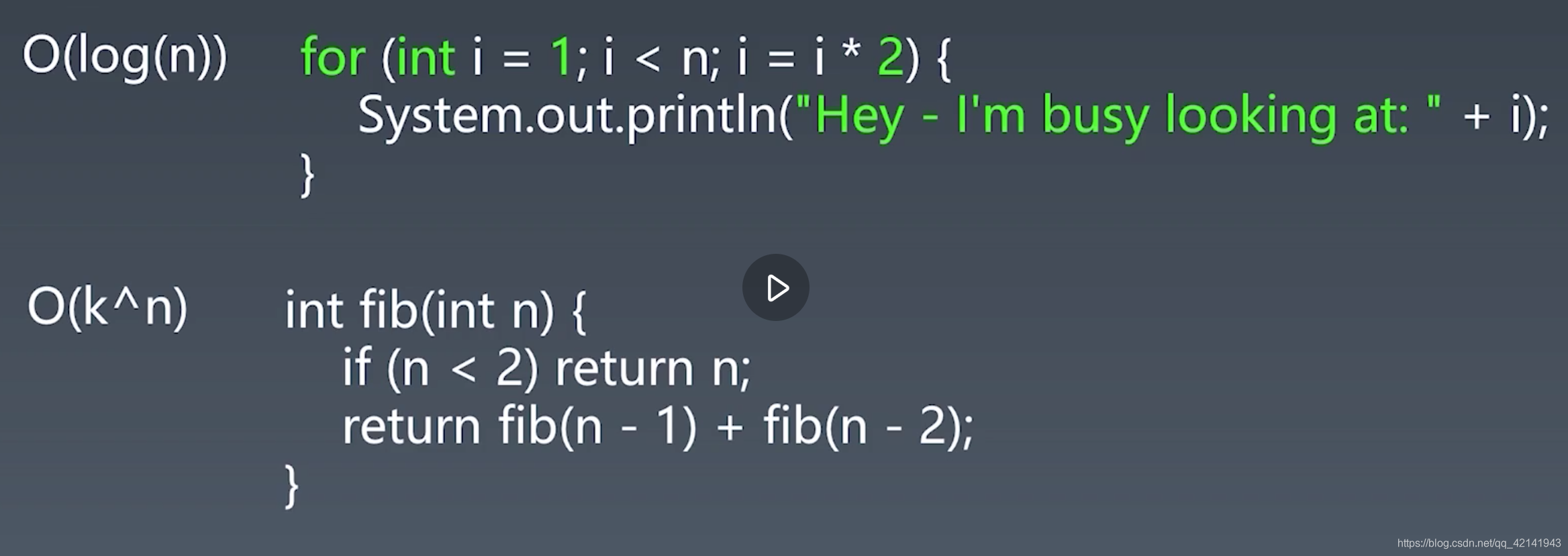
在这里插入图片描述

看一下结束条件, 和i的增长条件很自然得出i和n之间的关系即
i=log2(n), 而i刚好就是迭代次数也就是调用次数，因此调用次数与n的关系为调用次数=log2(n)，时间复杂度为对数复杂度
第二段代码, fib是斐波那契数列，n代表的是斐波那契数列中第n个数，n=0,fib(0)=0, fib(1)=1 有了这两项后就可以用递归的方式算出后续的. 在这里给出一个思路每一步都要调用前两步(包括2不包括0，1)因此首先算多少步会调用下面两步: n-2+1=n-1, 最后再加上最上面的那个即为2^(n-1)+1. 因此很明显时间复杂度为指数.

递归的时间复杂度当n较大是很高的因此用循环可能能变为线性如上.

1.3 递归的时间复杂度求解-Master Theory

1.31 主定理-Master Theory

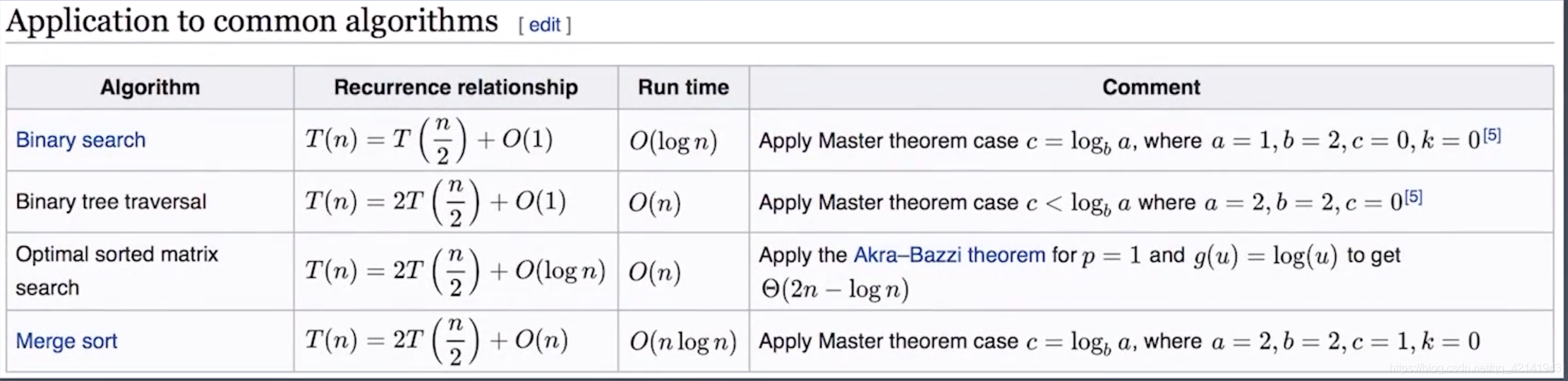
在这里插入图片描述

Binary Search-二分查找: 在一个有序数列里找到目标数，每次一分为二因此他的关系如图所示. 或者换言之, 从最底层扩容扩容i次一定等于数组长度n，i恰好就是正序的时候的查找次数, 二扩容每次扩两倍因此2^i=n 因此i=log2n.
Binary tree traversal-二叉树遍历：每个节点访问一次且仅访问一次因此为常数
Optimal sorted matrix-二维排好序的矩阵的二分查找: 为常数(一维数组为对数)
Merge sort-归并排序: 为nlogn. 二分法为查找归并为排序.

1.32 常考情形

复杂度为O(n)的
二叉树的前中后序排列
时间复杂度为O(n)其中n为节点个数，可以说是根据主定理，也可以说是每个节点访问一次且仅访问一次，因此调用次数一定线性与节点个数.
图的遍历
DFS深度优先和BFS广度优先搜索算法.
上面给的4种主定理常用情景.

2. 空间复杂度

2.1 基本概念

和存储数据有关:

数组的长度
一位数组根据传入的n空间复杂度就是O(n).
二维数组即矩阵方阵的情况下就是O(n^2).
递归的深度
递归的最深深度就是空间复杂度, 如果递归里又开了数组那么两者间的最大值就是空间复杂度.

2.2 实战

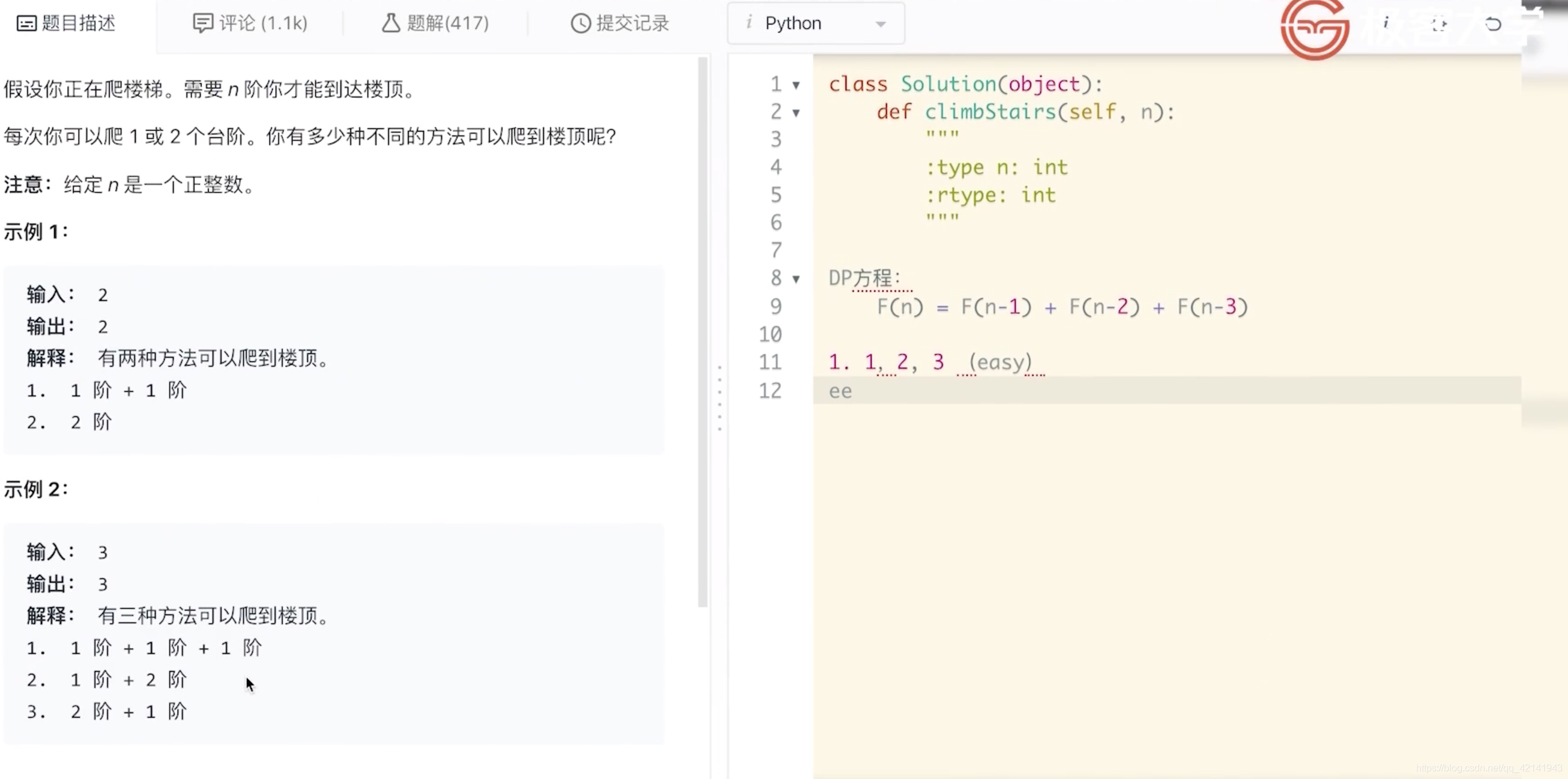
在这里插入图片描述
爬楼梯问题的两种解法

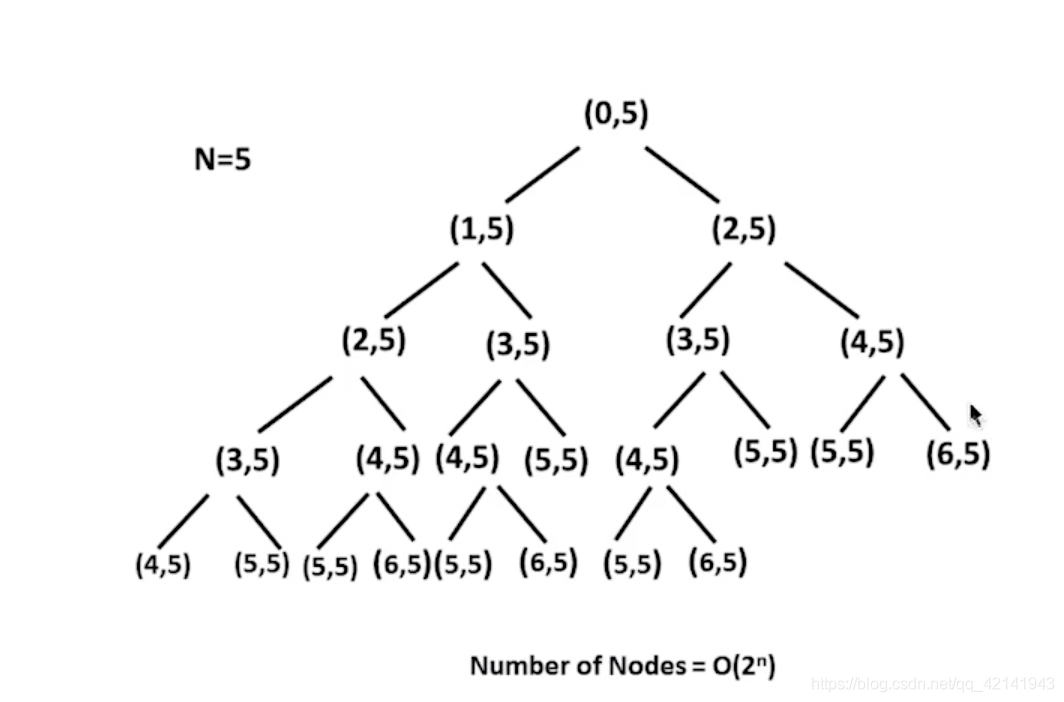
暴力法左边上一阶右边上两阶，一次扩充为2因此为2的n次方的时间复杂度，而最深深度肯定为一层层上为n因此空间复杂度为O(n).

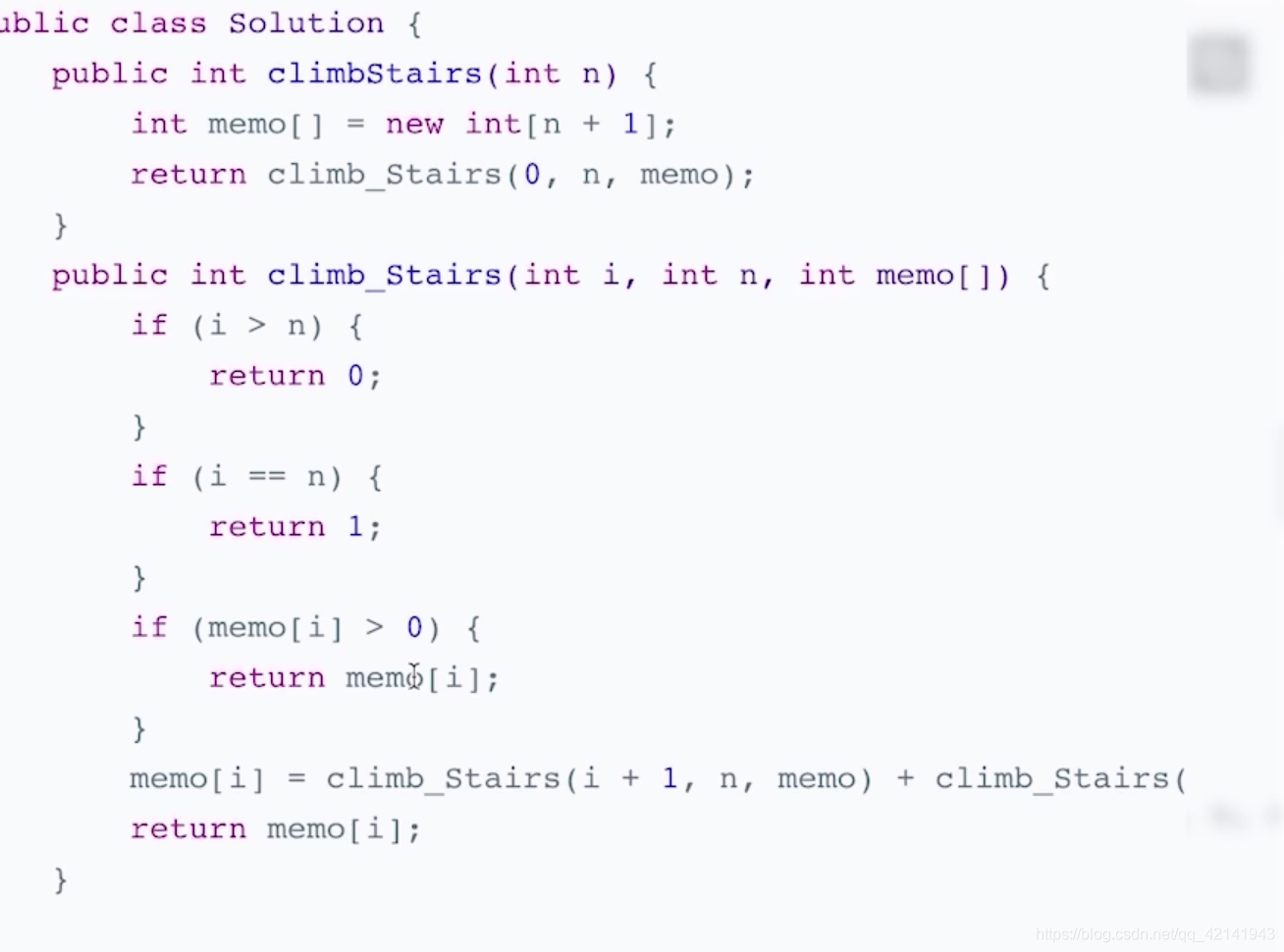
这里给递归中加入了一个数组用于存储计算过的值因此时间复杂度降为O(n)因为每个n对应的爬楼梯方法都只计算1次. 然而由于引入了数组空间复杂度却变了,数组的空间复杂度为O(n), 递归的空间复杂度也是O(n)因此总体来说还是O(n).