机器学习--Fisher线性判别

Fisher判别法介绍

Fisher判别法是判别分析的方法之一，它是借助于方差分析的思想，利用已知各总体抽取的样品的p维观察值构造一个或多个线性判别函数y=l′x其中l= (l1，l2…lp)′，x= (x1，x2，…，xp)′，使不同总体之间的离差(记为B)尽可能地大，而同一总体内的离差(记为E)尽可能地小来确定判别系数l=(l1，l2…lp)′。数学上证明判别系数l恰好是|B-λE|=0的特征根，记为λ1≥λ2≥…≥λr>0。所对应的特征向量记为l1，l2，…lr，则可写出多个相应的线性判别函数，在有些问题中，仅用一个λ1对应的特征向量l1所构成线性判别函数y1=l′1x不能很好区分各个总体时，可取λ2对应的特征向量l′2建立第二个线性判别函数y2=l′2x，如还不够，依此类推。有了判别函数，再人为规定一个分类原则(有加权法和不加权法等)就可对新样品x判别所属 [1] 。
Fisher判别法是根据方差分析的思想建立起来的一种能较好区分各个总体的线性判别法，由Fisher在1936年提出。该判别方法对总体的分布不做任何要求。
Fisher判别法是一种投影方法，把高维空间的点向低维空间投影。在原来的坐标系下，可能很难把样品分开，而投影后可能区别明显。一般说，可以先投影到一维空间(直线)上，如果效果不理想，在投影到另一条直线上(从而构成二维空间)，依此类推。每个投影可以建立一个判别函数 [2] 。

Fisher线性判别

Fisher分类器也叫Fisher线性判别（Fisher Linear Discriminant），或称为线性判别分析（Linear Discriminant Analysis，LDA）。LDA有时也被称为Fisher’s LDA。最初于1936年，提出Fisher线性判别，后来于1948年，进行改进成如今所说的LDA。
Fisher的基本思想是：
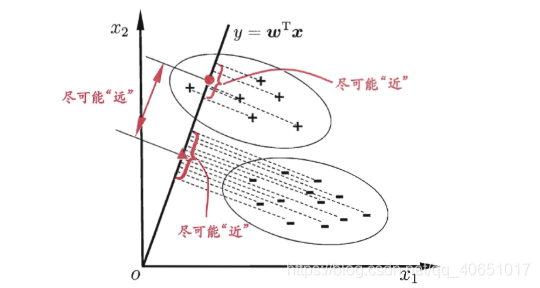
训练时，将训练样本投影到某条直线上，这条直线可以使得同类型的样本的投影点尽可能接近，而异类型的样本的投影点尽可能远离。要学习的就是这样的一条直线。
预测时，将待预测数据投影到上面学习到的直线上，根据投影点的位置来判断所属于的类别。

线性判别函数的一般形式可表示成

g(X)= $W^T$X+ $w_0$
​
其中

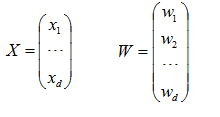
Fisher选择投影方向W的原则，即使原样本向量在该方向上的投影能兼顾类间分布尽可能分开，类内样本投影尽可能密集的要求。

Fisher准则函数的定义

几个必要的基本参量：

1. 在d维X空间
   （1）各类样本的均值向量mi
   
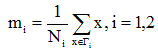
   （2）样本类内离散度矩阵Si和总样本类内离散度矩阵Sw
   
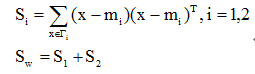
   其中Sw是对称半正定矩阵，而且当N>d时通常是非奇异的。（半正定矩阵：特征值都不小于零的实对称矩阵；非奇异矩阵：矩阵的行列式不为零）
   （3）样本类间离散度矩阵Sb
   
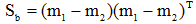
   Sb是对称半正定矩阵。
2. 在一维Y空间
   （1）各类样本的均值
   
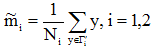
   （2）样本类内离散度 和总样本类内离散度
   
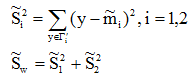
   我们希望投影后，在一维Y空间中各类样本尽可能分得开些，即希望两类均值之差越大越好，同时希望各类样本内部尽量密集，即希望类内离散度越小越好。
   Fisher准则函数定义
   

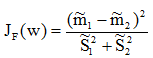
由各类样本的均值可推出：

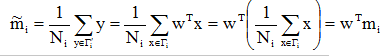
这样，Fisher准则函数JF(w)的分子可写成：

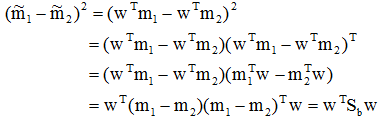
python代码实现

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt 
import seaborn as sns
path=r'./Iris.xls'
df = pd.read_csv(path, header=0)
Iris1=df.values[0:50,0:4]
Iris2=df.values[50:100,0:4]
Iris3=df.values[100:150,0:4]
m1=np.mean(Iris1,axis=0)
m2=np.mean(Iris2,axis=0)
m3=np.mean(Iris3,axis=0)
s1=np.zeros((4,4))
s2=np.zeros((4,4))
s3=np.zeros((4,4))
for i in range(0,30,1):
    a=Iris1[i,:]-m1
    a=np.array([a])
    b=a.T
    s1=s1+np.dot(b,a)    
for i in range(0,30,1):
    c=Iris2[i,:]-m2
    c=np.array([c])
    d=c.T
    s2=s2+np.dot(d,c) 
    #s2=s2+np.dot((Iris2[i,:]-m2).T,(Iris2[i,:]-m2))
for i in range(0,30,1):
    a=Iris3[i,:]-m3
    a=np.array([a])
    b=a.T
    s3=s3+np.dot(b,a) 
sw12=s1+s2
sw13=s1+s3
sw23=s2+s3
#投影方向
a=np.array([m1-m2])
sw12=np.array(sw12,dtype='float')
sw13=np.array(sw13,dtype='float')
sw23=np.array(sw23,dtype='float')
#判别函数以及T
#需要先将m1-m2转化成矩阵才能进行求其转置矩阵
a=m1-m2
a=np.array([a])
a=a.T
b=m1-m3
b=np.array([b])
b=b.T
c=m2-m3
c=np.array([c])
c=c.T
w12=(np.dot(np.linalg.inv(sw12),a)).T
w13=(np.dot(np.linalg.inv(sw13),b)).T
w23=(np.dot(np.linalg.inv(sw23),c)).T
#print(m1+m2) #1x4维度  invsw12 4x4维度  m1-m2 4x1维度
T12=-0.5*(np.dot(np.dot((m1+m2),np.linalg.inv(sw12)),a))
T13=-0.5*(np.dot(np.dot((m1+m3),np.linalg.inv(sw13)),b))
T23=-0.5*(np.dot(np.dot((m2+m3),np.linalg.inv(sw23)),c))
kind1=0
kind2=0
kind3=0
newiris1=[]
newiris2=[]
newiris3=[]
for i in range(29,49):
    x=Iris1[i,:]
    x=np.array([x])
    g12=np.dot(w12,x.T)+T12
    g13=np.dot(w13,x.T)+T13
    g23=np.dot(w23,x.T)+T23
    if g12>0 and g13>0:
        newiris1.extend(x)
        kind1=kind1+1
    elif g12<0 and g23>0:
        newiris2.extend(x)
    elif g13<0 and g23<0 :
        newiris3.extend(x)
#print(newiris1)
for i in range(29,49):
    x=Iris2[i,:]
    x=np.array([x])
    g12=np.dot(w12,x.T)+T12
    g13=np.dot(w13,x.T)+T13
    g23=np.dot(w23,x.T)+T23
    if g12>0 and g13>0:
        newiris1.extend(x)
    elif g12<0 and g23>0:
       
        newiris2.extend(x)
        kind2=kind2+1
    elif g13<0 and g23<0 :
        newiris3.extend(x)
for i in range(29,49):
    x=Iris3[i,:]
    x=np.array([x])
    g12=np.dot(w12,x.T)+T12
    g13=np.dot(w13,x.T)+T13
    g23=np.dot(w23,x.T)+T23
    if g12>0 and g13>0:
        newiris1.extend(x)
    elif g12<0 and g23>0:     
        newiris2.extend(x)
    elif g13<0 and g23<0 :
        newiris3.extend(x)
        kind3=kind3+1
correct=(kind1+kind2+kind3)/60
print("样本类内离散度矩阵S1：",s1,'\n')
print("样本类内离散度矩阵S2：",s2,'\n')
print("样本类内离散度矩阵S3：",s3,'\n')
print('-----------------------------------------------------------------------------------------------')
print("总体类内离散度矩阵Sw12：",sw12,'\n')
print("总体类内离散度矩阵Sw13：",sw13,'\n')
print("总体类内离散度矩阵Sw23：",sw23,'\n')
print('-----------------------------------------------------------------------------------------------')
print('判断出来的综合正确率：',correct*100,'%')

我们还可以采用贝叶斯、BP神经网络、K-means等算法做鸢尾花数据集（Iris）线性分类
有兴趣的小伙伴可以在网上查找相关文章进行了解！！