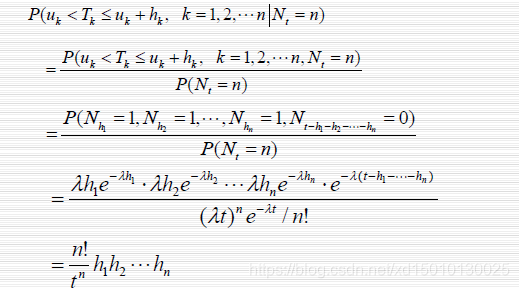第四章泊松过程2

1泊松过程的等价定义

1.1定义

1. $N_0=0$
2. N是平稳的独立增量过程
   对于很小的h，有
3. $P\{N_{t+h}-N_t=1\}=\lambda h+o(h)$
4. $P\{N_{t+h}-N_t=0\}=1-\lambda h+o(h)$
   

1.2定理

1. 泊松过程必满足“0-1”律
2. 如果计数过程满足独立平稳增量且满足“0-1”律，则该过程为泊松过程

1.3例题

让这个例题卖个萌

解：

1. $T_{100}$
2. $E[T_{100}]=n/\lambda=100/5=20$
3. $\tau$服从指数分布， $f(\tau)=\lambda e^{-\lambda\tau}$
4. $E[\tau_n]$

2泊松过程到达的条件分布

2.1仅有一个点到达的情况

设 $N=\{N_t,t\geq 0\}$服从泊松分布，那么在 $N_t=1$的条件下，过程的第一个随机点到达的时间 $T_1$服从 $[0,t_1]$上的均匀分布即
$P(T_1<s|N_t=1)=s/t$
证明：
$P(T_1<s|N_t=1)=\frac{P(T_1<s,N_t=1)}{P(N_t=1)}=\frac{P(N_s=1,N_t-N_s=0)}{P(N_t=1)}=\lambda se^{-\lambda s}e^{-\lambda (t-s)}/\lambda te^{-\lambda t}=s/t$

2.2更一般的情况

设 $N=\{N_t,t\geq 0\}$服从泊松分布，那么在 $N_t=n$的条件下，随机点的n个到达时刻 $T_1<T_2<...<T_n$有以下联合概率密度函数：
$p(u_1,u_2,...,u_n)=\frac{n!}{t^n}$
证明：

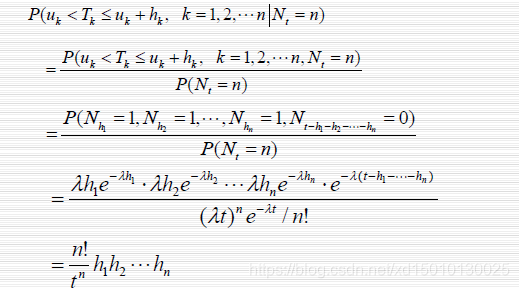
所以 $p(u_1,u_2,...,u_n)=\frac{n!}{t^n}$

2.3例题