一、单位根序列(非平稳序列)
当 d=0 时,ARIMA(p,d,q)模型是平稳的。模型的可逆性只与模型移动平均部分的算子方程的根有关,只要算子方程 的根在单位圆外,模型就是可逆的。反之,如果d≠0,算子方程有单位根,原序列非平稳。
算子方程为:Φ(B)(1 - B)d = 0 的根,其中Φ(B为下列等式。

与AR模型区别,自回归系数等于1则为单位根模型。若检测发现该模型属于单位根序列,不能直接进行回归,而需要进行差分或其他处理。
检验自回归系数是否为1方式:
- 回归方式
1)不带趋势的单位根检验
library(foreign) ; library(dynlm)
inven <- read.dta("http://fmwww.bc.edu/ec-p/data/wooldridge/inven.dta")
# variable to test: y =log(gdp)
inven$y <- log(inven$gdp)
inven.ts <- ts(inven)
# summary out of ADF regression
summary(dynlm( d(y) ~ L(y) + L(d(y)) + trend(inven.ts),data = inven.ts))
summary(dynlm( d(y) ~ L(y) + L(d(y)) ,data = inven.ts))
# automated ADF test using tseries :
library(tseries)
adf.test(inven$y , k =1) # adf检验该序列是否为单位根,
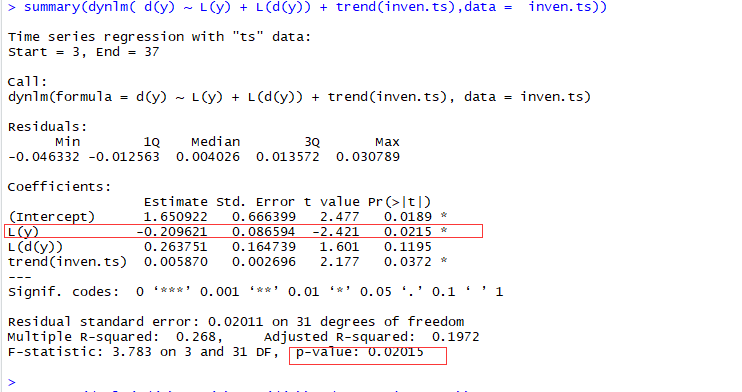
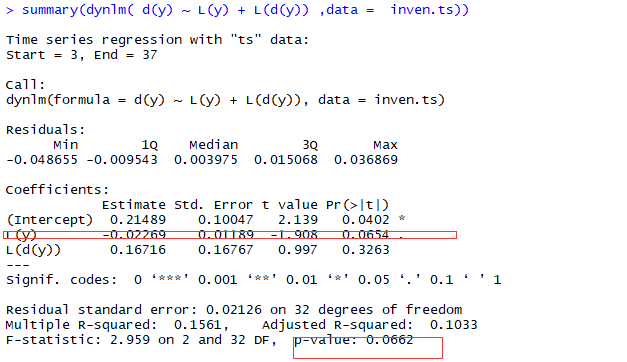
结果发现带趋势项的因变量的一阶差分项更显著,同时对y差分后Estimate项越接近0表示方程越好,同时在5%的水平adf检验的t值在-3.14,而-2.4521大于此值,不显著,说明存在单位根,其不是个平稳的序列。
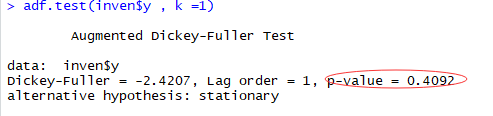
观察adf检验p值也得出不能拒绝原假设,存在单位根。
2)谬误回归
2个序列回归,可能会存在很强的显著性,但此显著性本质上不存在任何意义。
比如自建2个随机游走之间可能存在相关性,说其存在相关性,此为谬误回归。原因为此2个序列均为随机游走序列,均不平稳。
n <- 50
e <- rnorm(n)
a <- rnorm(n)
# independent random walks
x <- cumsum(a)
y <- cumsum(e)
#plot
plot(x , type = 'l' , lty=1, lwd =1)
lines(y, lty=2, lwd=2)
legend("topright" , c("x","y") , lty = c(1,2),lwd = c(1,2))
summary(lm(y~x))

- 对2个序列差分处理后,证明不存在显著性了

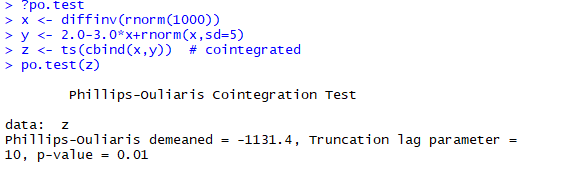
- po.test()检测
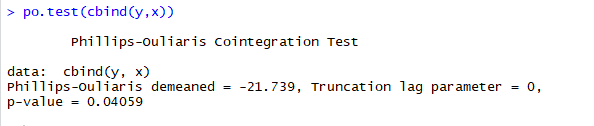
观察p值,大于0.05,则不能拒绝y与x相关是一个谬误回归
通过文档的例子,当y和x存在一定的关系是,p值小于0.05,证明不存在谬误回归