一、前言

线性分组码包括一大类的纠错编码在内，有汉明码、循环码、LDPC码等等，之前了解这些编码也是在网上搜搜资料，看看博客这样去学习，在网上搜索资料的时候发现一个问题，例如在看很多人写的汉明码博客时，很多人都一味的去追求“通俗易懂”，讲汉明码的构造和码字长度、怎么去校验和纠错等等方法时，很多都是直接拿个方法就来用，并没有从数学原理上去分析为什么校验位要选择哪些哪些位的组合，校验位为什么要放在码字的哪个哪个位置等等，我之前也是一脸的迷惑，虽然我知道要怎么去构造，怎么去用，但是为什么要这么构造，似乎只能说是因为我看到别人说要这么用，所以就这么用，然后发现这么用确实可以，构造方法很巧妙，为什么这么巧妙呢？怎么想到的呢？不知道。其实不懂得背后的真正原理，也只是看看热闹而已。纠错码是属于通信原理那一部分的范畴的，具体来说是《信息论与编码》课本上讲的东西，上学的时候没认真去学，因为工作需要，认为自己需要掌握这部分的知识，所以希望能从原理上去理解纠错编码，于是开始在网上搜各种各样的《信息论与编码》课程重新再自学一遍，在B站搜到了国防科技大学的信息论与编码课程，真是相见恨晚，我也不喜欢看各种各样的公式，但是这些理论就是需要数学公式的推导和证明，于是硬着头皮去学习了，相比于其他课程，这门课程涉及到的公式已经算是很简单的了，而且纠错码、压缩算法等等都是很实用的，说不定哪天项目上就能用上，就算没用上，在学习的过程中也为自己在很多方面的想法拓宽了思路，收益甚多。学习这些内容需要有基本的高数和线性代数基础。

二、纠错码的作用

假设我们要编码的数据有k位，用M来表示，称为信息位。由于要在编码后实现自动纠错的功能，所以需要添加一些额外的数据位来完成一些校验的算法，我们称这些额外添加的数据位为校验位（也称为冗余位），假设校验位长度为r，那么经过编码算法之后会生成一个长度为n=k+r位的数据，我们称为码字，用C来表示，如下图：

将我们原始的数据M经过编码算法编码为码字C后，我们将码字C发送到接收端，由于信息发送出去到接收端接收过程中，可能由于种种原因导致码字C中的某些数据位出错，所以接收端接收到的是错误的数据，我们假设为R，如下图：

由于我们传送的数据是经过精心编码后的数据，它比原始的数据要更加的长，经过解码算法的运算，即使存在错误我们也能够巧妙的识别并且算出原来正确的数据是什么，如下图：

二、线性分组码的定义

1、定义

线性分组码是一类很广泛的纠检错码，其码字的构造遵循严格的数学公式，而且都是线性的运算，所以这一类的码统称为线性分组码，线性分组码可以概括为如下的一个线性映射：

前面的映射函数指的是线性性质的映射，后面的GF(2)指的是伽罗华域，通俗来讲就是所有的数据位要么取0，要么取1，就是数据是二进制的形式。

描述一个线性分组码一般有个简便的记法，叫(n, k)线性分组码，k是原始数据的长度，n是原始数据经过编码后的码字长度。

2、鉴别

（1）判断下面的(5, 2)分组码是否为线性分组码

（M）信息组	（C）码字
00	11000
01	10101
10	01110
11	00011

由上面线性分组码的公式定义，我们直接令a和b为0，那么f(0) = 0，说明信息组元素全部为0的时候对应的码字也全0，但是上面信息组全0的时候对应的码字为11000，所以不符合线性性质，不是线性分组码。另外从这个推论还可以知道，线性分组码存在全0的码字，而且全0的信息组对应这个全0的码字。

其实上面的信息组（M）对应的码字（C）关系可以由如下公式来表示：

在二进制中的逻辑运算中，异或运算是线性的，而取反运算是非线性的，所以这个分组码的生成中存在非线性的运算过程，自然就不会是线性分组码了。

（2）判断下面的(5, 2)分组码是否为线性分组码

（M）信息组	（C）码字
00	00000
01	01011
10	10101
11	11110

将信息组进行各种各样的线性组合，得到的码字都会是这4个中的其中一个，所以是线性分组码。这里也得出一个结论，线性分组码的任何两个码字相加后得到的是另外一个码字。也就是说上面的4个码字，随便取两个相加（这里的二进制相加溢出后为0，而且不进位），得到的结果还是这4个码字中的其中一个。

这里再分析一个问题，我们的信息位有2位，有4中组合方式；码字对应也有4个，而且这4个码字是定死的，但是码字有5位，对于二进制来说5个比特可以表示2^5 = 32种状态，所以“浪费”了32 - 4 = 28种状态没去用，能用的码字称为可用码组，不能用的码字称为不可用码组。把码字理解为一个5维的向量，那么信息组就是一个2维的向量，可以使用的码字因为只有4种状态可以用，所以是5维向量空间中的一个二维子空间。推广来说：（n, k）线性分组码是一个n维线性空间的k维子空间。

三、生成矩阵

上面的推论已经描述了，（n, k）线性分组码是一个n维线性空间的k维子空间，n位的码字C由k位的信息组M经过一个线性映射来生成，我们把C看做一个n维的向量， $\vec{g}$ 看n维向量空间中的其中一个向量，那么有如下的公式：

上面的所有的 $\vec{g}$ 向量之间都不是线性相关的，其实就是k个n维向量空间中的基底，由这k个向量之间进行任意的线性组合，可以构成2^k种不同的码字。这些码字是与2^k个信息组一一对应的。

公式中的所有m是什么在使用过程中是确定的，C是对应生成的码字，所以只有 $\vec{g}$ 向量是不确定的，所以构造线性分组码的过程主要是去找k个线性无关的向量。再把上面的公式用矩阵运算来表达：

总的可以抽象写成：C = MG 的形式。C为1*n的码字矩阵，M为1*k的信息组矩阵，G为k*n的生成矩阵。生成矩阵G展开如下：

接下来分析一下生成矩阵的行和列代表什么意思。每一行是n维的，是一个基底，这k行就是k个基底，每一个码字都是由这k行的线性组合构成的，所以这里每一行其实也是2^k个码字中的一个码字。每一列是k维的，代表一个码字中对应位的生成规则，其实就是说明该码字中的这一位是由信息组的哪些位经过异或运算来得到的。

这里又引出了一个问题，原理上来说生成矩阵G是由k个线性不相关的n维向量构成的，那么其实G的每一行互相换下位置又可以得到一个新的矩阵，每一列互相换下位置又可以得到一个新的矩阵，那么G可以有很多种形式了？没错，这些都是可以使用的生成矩阵，而且有一点要注意，进行行变换的话不会改变码字空间，也就是原来会生成哪些码字，变换后的矩阵依然用的是这些码字；如果采用列变换的话会改变原来的码字空间，之前的一些可用码字会变为不可用码字，有些不可用码字会变为可用码字。为什么会这样呢？很好解释，行变换会改变码字中的每个位的生成规则，是k行中的某些行进行调换，而信息组有2^k个虽然哪一个信息组对应哪一个码字的规则可能会变化，但是总的来说会是之前的码字集合，这k个位置具有对称性；列变换打乱了n列的相对位置，也会改变码字中的每个位的生成规则，但是不具有k个位置的对称性，所以码字空间会改变。

对于同一个线性分组码，有那么多的生成矩阵，其实它们的纠错性能是一样的，那么为了好描述，所以约定了一个叫“系统码”的概念，规定了将生成矩阵G化成下面的形式：

系统码由两个子矩阵I和P构成，I是k*k的单位阵，P是k*r的矩阵，其实系统码也不是唯一的，把P矩阵中的列互相换一换就又不一样了。

大家肯定会疑惑为什么非要化成这种形式，因为化成这种形式有一个很大的好处，下面会说到。

四、校验矩阵

一般设计一个线性分组码都是先设计校验矩阵的，记为H，校验矩阵确定后，线性分组码的纠错能力就确定了。用上面线性分组码的鉴别中举的例（2）来具体说明什么是校验矩阵。

（M）信息组	（C）码字
00	00000
01	01011
10	10101
11	11110

由上面的生成规则可以得出三个方程：

把东西都移到左边来（二进制的模2加法和减法都是一样的效果，所以减法全部用加法表示）：

由线性代数的基础知识，可以把方程组写成矩阵的形式，如下：

把最左边的矩阵称为校验矩阵（一致校验矩阵），记为H，上面的式子可以简化写成 $H{C}^T = 0^T$ ，变化一下写成 $CH^{T}=0$ 。校验矩阵实质上就是一个校验方程组的系数矩阵，其中的每一行表示一个约束方程，每一列表示某位码元的受约束情况。可以把接收到的码字R（C 在传输中出了错变成 R）进行以上运算，如果结果为0矩阵，则传输过程中没有出现错误，否则就出现了错误。说白了就是检查这三个方程还能不能满足，不能满足说明出错了。

当然，校验矩阵H把行和列随便换换就又可以得到不同的校验矩阵了，那么又约定一个标准的校验矩阵形式如下：

五、生成矩阵和校验矩阵的关系

我们拿上面的例（2）来分析，在上面已经得出了校验矩阵H如下：

生成矩阵G是k*n维的，校验矩阵H是r*n维的，根据矩阵乘法的性质G是可以和 $H^{T}$ 相乘的，那么这两个矩阵相乘有什么意义呢？上面已经说了G的每一行都是一个码字，H的每一行表示一个约束方程，G和 $H^{T}$ 相乘的过程其实就是G的每一行和H的每一行相乘，G中的每一行相当于是方程的解，H相当于是方程组，就跟数学解方程是一样的，如果方程的解全对的话当然满足方程组的所有校验方程，G的每一行乘H的每一行当然得到的结果是0，即G和 $H^{T}$ 相乘后得一个k*r维的全0矩阵。如下公式：

因为校验矩阵可以写成两部分的形式即 $Q_{rk}$ 和 $I_{r}$ ，生成矩阵也可以写成两部分的形式即 $I_{k}$ 和 $P_{kr}$ ，所以可以推出 $Q_{rk}$ 和 $P_{kr}$ 互为转置矩阵的关系，即：

那么校验矩阵和生成矩阵的关系就出来了，比方说我们设计好了一个标准校验矩阵，可以直接推出对应的生成矩阵，如下：

对于例（2）来说，生成矩阵如下：

大家可以根据C = MG的关系去验证一下看下G的结果是否正确。

六、线性分组码的译码

上面讲的都是怎么去编码，知道编码的方法后，我们可以用编码后的码字进行信道的传输（具体什么传输方式不管），然后接收端收到的码字可能有些比特位发生了错误（翻转），怎么去译码而得到正确的结果呢？

（1）标准阵列式译码

标准阵列式译码需要构造一个包含所有码字（可用码字和不可用码字都包含在内的 $2^{n}$ 个码字）的码表，码表的每一列在译码时都译为列首的那个可用码字，是一种最大似然译码，具体方法举个例子。

有下面的（4,2）线性分组码，各个码字的生成规则如下：

当信息元 $(M_{1},M_{0})$ 分别为（00）、（01）、（10）、（11）时，对应的码字为（0000）、（0111）、（1010）、（1101），列出如下的一个表格：

	$C^{(0)}$	$C^{(1)}$	$C^{(2)}$	$C^{(3)}$
可用码组	0000	0111	1010	1101

接下来选一个译码码字以外的含1个数最少的禁用码字，我们先选（1000），按照1在最左边的规则去优先选择，将它排在 $C_{0}$ 这一列的下面，然后 $C_{1}$ 、 $C_{2}$ 、 $C_{3}$ 这三列都用第一行的译码码字与（1000）进行异或运算得到各自第二行的禁用码字，如下表所示：

	$C^{(0)}$	$C^{(1)}$	$C^{(2)}$	$C^{(3)}$
可用码组	0000	0111	1010	1101
禁用码组	1000	1111	0010	0101

接下来再选取一个当前表中没有的含1个数最少的禁用码字，为（0100），将它放在 $C_{0}$ 列的第三行，，然后其余3列如之前类似操作，得到如下的表格：

	$C^{(0)}$	$C^{(1)}$	$C^{(2)}$	$C^{(3)}$
可用码组	0000	0111	1010	1101
禁用码组	1000	1111	0010	0101
禁用码组	0100	0011	1110	1001

接下来再选取（0001）做类似操作，为什么不选0010呢，因为0010在表中已经有了，所以就不选了。如下表：

	$C^{(0)}$	$C^{(1)}$	$C^{(2)}$	$C^{(3)}$
可用码组	0000	0111	1010	1101
禁用码组	1000	1111	0010	0101
	0100	0011	1110	1001
	0001	0110	1011	1100

到这里， $2^{n}$ = $2^{4}$ = 16个码字就已经全部列在表中了，加入在经过信道传输后，我们接受到一个码字R为（1111），我们就译码为列首的可用码字（0111），接受到R为（1100）同理译码为（1101）。不难发现，其实在每一列中，列首的码字和其余码字其实都只有一个比特位不同而已，不同列的码字和列首码字最少都有两个比特位不同，这个译码原理就很简单了，就是接收到的码字R和哪个可用码字“长得最像”，就译码为哪个可用码字，这就是最大似然译码的原理。

这里再介绍一个概念，在数学中，上表中的可用码组称为“子群”，对应产生的禁用码组称为“陪集”， $C_{0}$ 这一列是“陪集”的第一列，称为“陪集首”。

回到实际应用的问题上来，用标准阵列式译码的方法，接收端想要译码，我们至少需要在内存中构造一个 $2^{n}$ 大小的表格来存放这些译码的映射关系，当然，你可能会说你想到了一个比较简单的存储的办法，我们先不考虑这个，在实际应用中的线性分组码取的n是很大的几百上千，2的指数次方这个数字有多大完全不敢想，存表方法肯定是不实用了，怎么办呢？

（2）伴随式译码

在上面讲生成矩阵和校验矩阵的时候已经介绍了它们之间有个关系如下：

其实每一个可用码字C都满足这样的关系即 $CH^{T} = 0$ ，所以我们在接收到码字R后，去和 $H^{T}$ 做矩阵乘法，如果得到的向量是0向量，那么这个码字R是可用的码字，那么表示接收正确没有在传输过程中出现错误，如果不是0向量，那么肯定是出错了。那么接下来要解决的一个问题是，我知道出错了，但是我要怎么知道是哪个位出错了呢？

接下来引入一个伴随式的概念：

R是1*n维的向量，H是r*n维的向量，那么S是1*r维的向量。即 $S = (S_{r-1},...,S_{1},S_{0})$ 。为了计算上例中的伴随式S，我们先写出校验矩阵H如下：

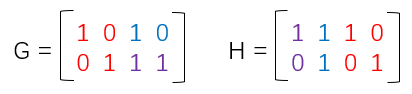
然后我们用标准阵列译码表中的每个码字都和校验矩阵的转置相乘，会发现每一行的伴随式S其实都是相同的，为什么会这样呢？其实这是必然的。

接下来再引入一个概念：C是发送端的原始码字，R是经过信号传输后的加入了一些错误的码字，那么其实可以把信道传输中加入的错误定义为E，于是C、R和E之间存在着如下的关系：

根据这个式子可以得到新的伴随式为：

从上式得出一个结论，伴随式S只与错误图样E和校验矩阵H有关，和具体发送端传了什么码字过来是没有任何关系的。对应到标准阵列式译码表上，其实“陪集首”就是这里所说的错误图样E，陪集首后面的列都是与陪集首相异或运算后得到的，相当于是在码字中引入这个错误图样，即每一行的错误图样都是一样的，又因为伴随式只与错误图样有关，所以证明了每一行的码字生成的伴随式是一样的，我们整理成如下的表格：

	$C^{(0)}$	$C^{(1)}$	$C^{(2)}$	$C^{(3)}$	S
可用码组	0000	0111	1010	1101	00
禁用码组	1000	1111	0010	0101	10
	0100	0011	1110	1001	11
	0001	0110	1011	1100	01

所以到这里我们就明白了根据接收到的码字R和校验矩阵相乘可以得到伴随式S，由S又可以推出错误图样E，知道了错误图样就知道了哪个比特位出错了，于是将这个比特位翻转过来，就得到了正确的码字。

伴随式译码其实还是描述了标准阵列译码的过程，只是伴随式译码不需要再去存储这张大表格了，得以在实际中运用，所以线性分组码的译码基本都是采用伴随式译码，伴随式译码也是一种最大似然译码。

这里再说一点，细心的朋友可能会发现，上面的例子中，如果码字 $C(C_{3}C_{2}C_{1}C_{0})$ 中的 $C_{1}$ 出现了翻转，岂不是不能纠正？是的，的确纠正不了，我们可以算一下伴随式是（10），接收端会认为是 $C_{3}$ 出错了，于是译码错误。这就涉及到目前这个（4,2）线性分组码的纠错能力的问题了，这个在下一篇博客里面详细介绍。

心城追梦

原创文章 22 获赞 29 访问量 1万+

关注私信

纠错码专题——线性分组码（1）

目录