一、前言

本文是在我的上一篇博客基础上展开的描述，上一篇介绍了线性分组码的概念、生成矩阵和校验矩阵，简单的举了几个例子，在最后的一个（4,2）线性分组码例子上，码字 $C_{1}$ 如果出现了错误是无法纠正的，原因是该线性分组码的纠错能力的限制，这一篇详细说明其中的原理，过程中会尽量多举例子，查资料过程中找到了一个写的很棒的PPT，附在文末的资料里了。

二、线性分组码的最小距离、检错和纠错能力

想要了解线性分组码的检错和纠错能力，即一个已知的线性分组码，怎么知道能纠正多少个错误？能检查出多少个错误？就必须要理解下面提到的概念。

1、汉明重量

汉明重量W：码字中非0码元符号的个数，称为该码字的汉明重量。在二元线性码中，码字重量就是码字中“1”的个数。同时，线性分组码中非0码字重量的最小值叫做该码的最小重量。举个例子：一个码字U=0011101，那么这个码字的汉明重量为4。

2、汉明距离

在 (n,k)线性码中，两个码字 U、V 之间对应码元位上符号取值不同的个数，称为码字 U、V 的汉明距离。举个例子：(7,3) 码的两个码字 U=0011101,V=0100111之间第2、3、4和6位不同。因此，码字 U 和 V 的汉明距离为4。

3、最小距离

在 (n,k) 线性码的码字集合中，任意两个码字间汉明距离的最小值，叫做码的最小距离，一般记为 $d_{min}$ ，在线性分组码的研究中，该参数极为重要，直接影响纠检错能力。码的最小距离越大，码的抗干扰能力就越强。举个例子：

（M）信息组	（C）码字
00	00000
01	01011
10	10101
11	11110

上面为（5,2）线性分组码的信息元和码字的对应关系，可以知道整个码字空间只有这4个码字，我们两两码字之间算一下汉明距离，比较了 $C_{4}^{2}=6$ 次之后可以知道最小汉明距离为3。其实不用去比较那么多次的，因为上一篇博客已经介绍过了，每两个码字相加之后得到的向量其实还是另外一个码字，而两个码字相加后新码字中“1”的个数其实就是它们之间的汉明距离，问题就被转化成了求所有码字中最少1的个数，当然全0的码字不能算在里面，所以一眼看上去，01011和10101这两个码字中含“1”的个数都是3，都是最少的，所以最小距离 $d_{min}=3$ 。

4、汉明球

为什么弄个汉明球的概念进来，因为这便于理解线性分组码的纠检错能力的最本质原理。一个码字C我们可以理解是三维空间中的一个点，以t为半径可以绕着该点围出一个三维球体，我们称这个球为汉明球。一个线性分组码有很多的码字，每一个码字都可以理解为三维空间中的一个点，每一个点都以t为半径围了一个球体，而且这些球体在三维空间中没有任何相接触（相交）的部分，任意两个汉明球不相交最大程度取决于任意两个码字之间的最小汉明距离dmin，如下图：

5、检错能力和纠错能力的定义

（1）检错能力：一个线性码能检出长度≤l 个码元的任何错误图样，称码的检错能力为 l。

（2）纠错能力：线性码能纠正长度≤t 个码元的任意错误图样，称码的纠错能力为 t。

（3）最小距离与纠错能力：(n,k) 线性码能纠 t 个错误的充要条件是码的最小距离为：

即：

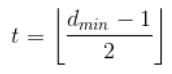
其中 $\left \lfloor X \right \rfloor$ 表示对X向下取整数。为什么是这样的呢？还是看这个图：

假定 $d_{min}=5$ ，那么图中两个点V和U的距离为5，在不想交的情况下，围绕着这两个点以整数t为半径画两个圆，这两个圆的最大半径t为多少呢？肯定是2，因为V和U相当于是线性分组码的两个合法码字，它们连线中间的4个点相当于是码字出错后的一些不合法码字，那么当这些不合法的码字离V的距离小于等于2的时候（在V球内），我们译码为码字V，同理当接收到的码字落在U球内时，我们译码为码字U，这样假定发送端发送的码字是V，然后错了两个bit的数据之后到发送端变成了R，V和R的距离为2，所以我们把R译码为V，就达到了把错误纠正回来的目的了。

（4）最小距离与检错能力：(n,k) 线性码能够发现 l 个错误的充要条件是码的最小距离为

我们还拿这个图举例子，但是进行一点改动，点U的位置变了：

假定 $d_{min}=3$ ，V和U的距离为3，那么只要接收到的码字R不和V或者U点重合，落在了它们之间的两个点上了，先不管最后译码成谁，只要不和V或U重合就一定是出错了，所以达到了检错的目的，检错能力是2。

再来个例子：

假定 $d_{min}=4$ ，那么V和U两个点间的距离为4，它们中间还有三个点，假设码字V错了3个bit变成R，也还离U的距离为1，可以被检测出来出错了。对U来说也是一样的。

（5）最小距离与检、纠错能力：(n,k) 线性码能纠 t 个错误，并能发现 l 个错误 (l>t) 的充要条件是码的最小距离为

当 (n,k) 线性码的最小距离 dmin 给定后，可按实际需要灵活安排纠错的数目。例如，对 dmin=8 的码，可用来纠3检4错，或纠2检5错，或纠1检6错，或者只用于检7个错误。

三、解决实验中的问题

下面我们来解决上一篇博客中最后遗留下来的问题，为什么 $C_{1}$ 位出错了会纠不回来？原题是这样的：

一个（4，2）线性分组码的生成矩阵和校验矩阵如下：

所有合法码字 $C_{3}C_{2}C_{1}C_{0}$ 如下：

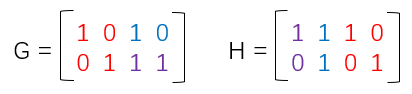
	$C^{(0)}$	$C^{(1)}$	$C^{(2)}$	$C^{(3)}$
可用码组	0000	0111	1010	1101

由本文介绍的知识知道1010这个码字的重量是非0码字外汉明距离最小的了为2，那么这个线性分组码的最小距离 $d_{min}=2$ ，即能纠0个错误，检1个错误。当然有人会有疑问？在使用过程中不是就 $C_{1}$ 出错了纠不了而已吗？其他1个错误的情况都能纠啊！这里要理清楚一个概念，一个码的纠错能力为t，是描述的在发生t个错误的所有情况下都必定能够纠正回来，但是上面这个分组码存在一个情况纠不了，所以不能说纠错能力为1。虽然纠不了，但是可以检测出来发生了错误，所以检测能力为1。

四、参考资料

线性分组码详解.ppt

链接：https://pan.baidu.com/s/1yTZxYOn2ct2QLlGBcARRxg 提取码：c7nx

心城追梦

原创文章 22 获赞 29 访问量 1万+

关注私信

纠错码专题——线性分组码的纠错能力

目录

一、前言

二、线性分组码的最小距离、检错和纠错能力

三、解决实验中的问题

四、参考资料

猜你喜欢