Crossing Number of Graphs 读书笔记

Page 3-9

1 The Conjectures of Zarankiewicz and Hills

说明： 个人笔记, 勿过度参考.
正文

1.1 Drawings with Crossings

In his “Perplexities” column for The Strand Magazine, Henry Dudeney posed a puzzle he called “Water, Gas, and Electricity”, accompanied by the illustration in Figure 1.1. Is it possible, he asked, that A, B, and C each have access to (W) ater, (G)as, and (E)lectricity, without their paths crossing?

We would now answer that a solution would require a planar drawing of a K3,3 which we know to be impossible by Kuratowski’s theorem (Appendix A reviews the basics of topological graph theory).

笔记：
这是交叉数的起源问题， $K_{3,3}$ 是否存在平面画法？简单的我们可以依据 Kuratowski’s theorem 知道不存在. 当然了，还可以借助一些平面图的不等式去证明.

那么， 何为 Kuratowski’s theorem ？

Kuratowski’s theorem
A finite graph is planar if and only if it does not contain a subgraph
that is a subdivision of K5 (the complete graph on five vertices)
or of K3,3 (complete bipartite graph on six vertices)

注：上述定理图的subdivision 定义：
In general, a subdivision of a graph G (sometimes known as an expansion[1]) is a graph resulting from the subdivision of edges in G. The subdivision of some edge e with endpoints {u,v} yields a graph containing one new vertex w, and with an edge set replacing e by two new edges, {u,w} and {w,v}.
For example, the edge e, with endpoints {u,v}:

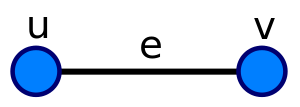
can be subdivided into two edges, e1 and e2, connecting to a new vertex w:

图的subdivision 是描述图论意义下图的同胚的含义的核心工具.
two graphs $G$ and $G'$ are homeomorphic if there is a graph isomorphism from some subdivision of $G$ to some subdivision of $G'$.

Henry Dudeney 也意识到这一点，于是他提供了另外一个次一点的方案。

显然： 这是一种退而求其次的办法，虽然各条路的确不交叉了，可是
c和 w 的路经过了A. 这也不符合愿意.
为了避免一些规定上不同导致的没必要的歧义，书本事先给出了详细的公认的规定。

正文

1. In a drawing of a graph, every vertex is assigned a different location, and edges are drawn as simple curves between the locations assigned to their end-points.
   每个顶点放在不同位置.

2. If two edges intersect finitely often, and an edge does not contain a point in its interior, then intersections between two curves are either a common endpoint, a crossing, or a touching point.
   边与边的交点分为3类. 第二类是本书重点研究的.
   

3. A drawing is normal, if every pair of edges has at most a finite number of intersections, there are no touching intersections, and no crossing belongs to more than two edges. We will always assume that drawings are normal, unless clearly stated otherwise.

要求： 1. 两条交叉的边交叉次数是有限的;
2 不存在 touching point
3 交叉点只能属于两条边. 不存在三条或者更多共一个交叉点.

Remark 1.1. Why do we not allow more than two edges crossing in a point? A possible answer is not necessary: ​​if k edges cross at the intersections (between two pairs of edges), and the same amount can be reached by slightly perturbing the edges (as observed by Tait [330] in 1877, see also Lemma A.23) If we want to count the points where multiple edges intersect as a single intersection, we get the concept of degenerate intersection number, which is the subject we do not pursue [248].

笔记：
如果 $k$ 条边共一个顶点， 那么我可以视为 $k$ 条边 两两相交退化情形，这是可以通过微小的调整做到的（Lemma A.23, 这种情况我们可以规避掉.

A drawing is good if edges do not have self-crossings (they are simple curves), and every pair of edges has at most one intersection (including a shared endpoint). In particular, adjacent edges do not cross, and independent edges cross at most once.
即下面三种不存在.

Normal 画法第三类图可以出现，因为他要求地是有限次即可.

正文：

Definition 1.2 (Crossing Number).
The crossing number, cr(D), of a drawing D is the number of crossings in D.
The crossing number, cr(G), of a graph G is the smallest cr(D) of any drawing D of G. We say a drawing D of G is cr-minimal, or that D realizes cr(G), if cr(D) = cr(G).

Lemma 1.3. I
If a drawing is not good, we can redraw it so it becomes good, the crossing number of the drawing decreases, and redrawn edges are routed arbi-trarily close to edges of the original drawing. In particular, every cr-minimal drawing of a graph is good.

笔记：
Lemma 1.3. 说明下面道理。 如何把不好的画法变成好的画法。
如果图不是好画法，我们可以对其进行重新绘制，使其变得良好，使得图的交叉数减少，并且重新绘制的边沿任意方向布线，十分接近原始图的边。 特别是，每个 cr 最小的图形绘制都是好的。

Proof. Suppose D is a drawing of G which is not good.

1. If D has a self-crossing, it can be removed by locally rerouting the edge close to the self-crossing; see Figure 1.3. (We could also short-cut the edge at the self-crossing; this is fine for the purposes of this proof, but sometimes we need to keep all pieces of an edge to satisfy some other condition.)
   
   自环消除，两种方法，一种自然非常近的分开，第二种直接去掉，如下图所示：但是有时候为了保证边的曲线尽可能都保存不被损坏，采用第一种.

2.