在分类问题中,你要预测的变量
y
y
y Logistic Regression ) 的算法。
我们从二元的分类问题开始讨论。
我们将因变量(dependent variable )可能属于的两个类分别称为负向类(negative class )和正向类(positive class ),则因变量
y
∈
0
,
1
y\in {0,1 \\}
y ∈ 0 , 1
但对于线性回归问题来说,函数的输出值可能大于1也可能小于0。所以不可能实现。所以我们研究逻辑回归。
在Classification 中我们提到怎么使分类器的输出值在0和1之间,由此我们提出一个假设:
h
θ
(
x
)
=
g
(
θ
T
X
)
∈
[
0
,
1
]
h_\theta(x)=g(\theta^TX)\in[0,1]
h θ ( x ) = g ( θ T X ) ∈ [ 0 , 1 ]
其中:
X
X
X
g
g
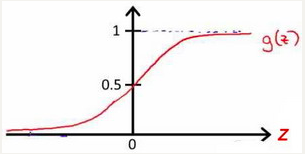
g logistic function )是一个常用的逻辑函数为S 形函数(Sigmoid function ),公式为:
g
(
z
)
=
1
1
+
e
−
z
g\left( z \right)=\frac{1}{1+{{e}^{-z}}}
g ( z ) = 1 + e − z 1
扫描二维码关注公众号,回复:
11068925 查看本文章
h
θ
(
x
)
h_\theta \left( x \right)
h θ ( x ) estimated probablity )即
h
θ
(
x
)
=
P
(
y
=
1
∣
x
;
θ
)
h_\theta \left( x \right)=P\left( y=1|x;\theta \right)
h θ ( x ) = P ( y = 1 ∣ x ; θ )
x
x
x
h
θ
(
x
)
=
0.7
h_\theta \left( x \right)=0.7
h θ ( x ) = 0 . 7
y
y
y
y
y
y
P
(
y
=
1
∣
x
;
θ
)
+
P
(
y
=
0
∣
x
;
θ
)
=
1
P\left( y=1|x;\theta \right)+P\left( y=0|x;\theta \right)=1
P ( y = 1 ∣ x ; θ ) + P ( y = 0 ∣ x ; θ ) = 1
在逻辑回归中,我们预测:
当
h
θ
(
x
)
>
=
0.5
{h_\theta}\left( x \right)>=0.5
h θ ( x ) > = 0 . 5
y
=
1
y=1
y = 1
当
h
θ
(
x
)
<
0.5
{h_\theta}\left( x \right)<0.5
h θ ( x ) < 0 . 5
y
=
0
y=0
y = 0
根据上面绘制出的 S 形函数图像,我们知道当
z
=
0
z=0
z = 0
g
(
z
)
=
0.5
g(z)=0.5
g ( z ) = 0 . 5
z
>
0
z>0
z > 0
g
(
z
)
>
0.5
g(z)>0.5
g ( z ) > 0 . 5
z
<
0
z<0
z < 0
g
(
z
)
<
0.5
g(z)<0.5
g ( z ) < 0 . 5
又
z
=
θ
T
x
z={\theta^{T}}x
z = θ T x
θ
T
X
>
=
0
{\theta^{T}}X>=0
θ T X > = 0
y
=
1
y=1
y = 1
θ
T
X
<
0
{\theta^{T}}X<0
θ T X < 0
y
=
0
y=0
y = 0
现在假设我们有一个模型:
并且参数
θ
\theta
θ
−
3
+
x
1
+
x
2
≥
0
-3+{x_1}+{x_2} \geq 0
− 3 + x 1 + x 2 ≥ 0
x
1
+
x
2
≥
3
{x_1}+{x_2} \geq 3
x 1 + x 2 ≥ 3
y
=
1
y=1
y = 1
x
1
+
x
2
=
3
{x_1}+{x_2} = 3
x 1 + x 2 = 3
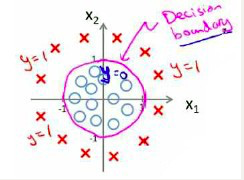
假使我们的数据呈现这样的分布情况,怎样的模型才能适合呢?
因为需要用曲线才能分隔
y
=
0
y=0
y = 0
y
=
1
y=1
y = 1
h
θ
(
x
)
=
g
(
θ
0
+
θ
1
x
1
+
θ
2
x
2
+
θ
3
x
1
2
+
θ
4
x
2
2
)
{h_\theta}\left( x \right)=g\left( {\theta_0}+{\theta_1}{x_1}+{\theta_{2}}{x_{2}}+{\theta_{3}}x_{1}^{2}+{\theta_{4}}x_{2}^{2} \right)
h θ ( x ) = g ( θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 1 2 + θ 4 x 2 2 )
我们可以用非常复杂的模型来适应非常复杂形状的判定边界。
对于线性回归模型,我们定义的代价函数是所有模型误差的平方和。理论上来说,我们也可以对逻辑回归模型沿用这个定义,但是问题在于,当我们将
h
θ
(
x
)
=
1
1
+
e
−
θ
T
x
{h_\theta}\left( x \right)=\frac{1}{1+{e^{-\theta^{T}x}}}
h θ ( x ) = 1 + e − θ T x 1 non-convexfunction )。
这意味着我们的代价函数有许多局部最小值,这将影响梯度下降算法寻找全局最小值。
线性回归的代价函数为:
J
(
θ
)
=
1
m
∑
i
=
1
m
1
2
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
2
J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{\frac{1}{2}{{\left( {h_\theta}\left({x}^{\left( i \right)} \right)-{y}^{\left( i \right)} \right)}^{2}}}
J ( θ ) = m 1 i = 1 ∑ m 2 1 ( h θ ( x ( i ) ) − y ( i ) ) 2
J
(
θ
)
=
1
m
∑
i
=
1
m
C
o
s
t
(
h
θ
(
x
(
i
)
)
,
y
(
i
)
)
J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{{Cost}\left( {h_\theta}\left( {x}^{\left( i \right)} \right),{y}^{\left( i \right)} \right)}
J ( θ ) = m 1 i = 1 ∑ m C o s t ( h θ ( x ( i ) ) , y ( i ) )
C
o
s
t
(
h
θ
(
x
(
i
)
,
y
(
i
)
)
=
1
2
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
2
=
{
−
l
g
(
h
θ
(
x
)
)
i
f
y
=
1
−
l
g
(
1
−
h
θ
(
x
)
)
i
f
y
=
0
Cost(h_\theta(x^{(i)},y^{(i)})=\frac{1}{2}(h_\theta(x^{(i)})-y^{(i)})^2=\begin{cases}-lg(h_\theta(x))&if&y=1 \\-lg(1-h_\theta(x))&if&y=0\end{cases}
C o s t ( h θ ( x ( i ) , y ( i ) ) = 2 1 ( h θ ( x ( i ) ) − y ( i ) ) 2 = { − l g ( h θ ( x ) ) − l g ( 1 − h θ ( x ) ) i f i f y = 1 y = 0
所以:
C
o
s
t
(
h
θ
(
x
(
i
)
,
y
(
i
)
)
=
−
y
×
l
g
(
h
θ
(
x
)
)
−
(
1
−
y
)
×
l
g
(
1
−
h
θ
(
x
)
)
Cost(h_\theta(x^{(i)},y^{(i)})=-y\times lg\left( {h_\theta}\left( x \right) \right)-(1-y)\times lg\left( 1-{h_\theta}\left( x \right) \right)
C o s t ( h θ ( x ( i ) , y ( i ) ) = − y × l g ( h θ ( x ) ) − ( 1 − y ) × l g ( 1 − h θ ( x ) )
带入代价函数得到:
J
(
θ
)
=
1
m
∑
i
=
1
m
[
−
y
(
i
)
log
(
h
θ
(
x
(
i
)
)
)
−
(
1
−
y
(
i
)
)
log
(
1
−
h
θ
(
x
(
i
)
)
)
]
J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{[-{{y}^{(i)}}\log \left( {h_\theta}\left( {{x}^{(i)}} \right) \right)-\left( 1-{{y}^{(i)}} \right)\log \left( 1-{h_\theta}\left( {{x}^{(i)}} \right) \right)]}
J ( θ ) = m 1 i = 1 ∑ m [ − y ( i ) log ( h θ ( x ( i ) ) ) − ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ]
J
(
θ
)
=
−
1
m
∑
i
=
1
m
[
y
(
i
)
log
(
h
θ
(
x
(
i
)
)
)
+
(
1
−
y
(
i
)
)
log
(
1
−
h
θ
(
x
(
i
)
)
)
]
J\left( \theta \right)=-\frac{1}{m}\sum\limits_{i=1}^{m}{[{{y}^{(i)}}\log \left( {h_\theta}\left( {{x}^{(i)}} \right) \right)+\left( 1-{{y}^{(i)}} \right)\log \left( 1-{h_\theta}\left( {{x}^{(i)}} \right) \right)]}
J ( θ ) = − m 1 i = 1 ∑ m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ]
证明如下:
Repeat {
θ
j
:
=
θ
j
−
α
∂
∂
θ
j
J
(
θ
)
\theta_j := \theta_j - \alpha \frac{\partial}{\partial\theta_j} J(\theta)
θ j : = θ j − α ∂ θ j ∂ J ( θ ) simultaneously update all )
求导后得到:
Repeat {
θ
j
:
=
θ
j
−
α
1
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
\theta_j := \theta_j - \alpha \frac{1}{m}\sum\limits_{i=1}^{m}{{\left( {h_\theta}\left( \mathop{x}^{\left( i \right)} \right)-\mathop{y}^{\left( i \right)} \right)}}\mathop{x}_{j}^{(i)}
θ j : = θ j − α m 1 i = 1 ∑ m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) (simultaneously update all )
J
(
θ
)
=
−
1
m
∑
i
=
1
m
[
y
(
i
)
log
(
h
θ
(
x
(
i
)
)
)
+
(
1
−
y
(
i
)
)
log
(
1
−
h
θ
(
x
(
i
)
)
)
]
J\left( \theta \right)=-\frac{1}{m}\sum\limits_{i=1}^{m}{[{{y}^{(i)}}\log \left( {h_\theta}\left( {{x}^{(i)}} \right) \right)+\left( 1-{{y}^{(i)}} \right)\log \left( 1-{h_\theta}\left( {{x}^{(i)}} \right) \right)]}
J ( θ ) = − m 1 i = 1 ∑ m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ]
h
θ
(
x
(
i
)
)
=
1
1
+
e
−
θ
T
x
(
i
)
{h_\theta}\left( {{x}^{(i)}} \right)=\frac{1}{1+{{e}^{-{\theta^T}{{x}^{(i)}}}}}
h θ ( x ( i ) ) = 1 + e − θ T x ( i ) 1
y
(
i
)
log
(
h
θ
(
x
(
i
)
)
)
+
(
1
−
y
(
i
)
)
log
(
1
−
h
θ
(
x
(
i
)
)
)
{{y}^{(i)}}\log \left( {h_\theta}\left( {{x}^{(i)}} \right) \right)+\left( 1-{{y}^{(i)}} \right)\log \left( 1-{h_\theta}\left( {{x}^{(i)}} \right) \right)
y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) )
=
y
(
i
)
log
(
1
1
+
e
−
θ
T
x
(
i
)
)
+
(
1
−
y
(
i
)
)
log
(
1
−
1
1
+
e
−
θ
T
x
(
i
)
)
={{y}^{(i)}}\log \left( \frac{1}{1+{{e}^{-{\theta^T}{{x}^{(i)}}}}} \right)+\left( 1-{{y}^{(i)}} \right)\log \left( 1-\frac{1}{1+{{e}^{-{\theta^T}{{x}^{(i)}}}}} \right)
= y ( i ) log ( 1 + e − θ T x ( i ) 1 ) + ( 1 − y ( i ) ) log ( 1 − 1 + e − θ T x ( i ) 1 )
=
−
y
(
i
)
log
(
1
+
e
−
θ
T
x
(
i
)
)
−
(
1
−
y
(
i
)
)
log
(
1
+
e
θ
T
x
(
i
)
)
=-{{y}^{(i)}}\log \left( 1+{{e}^{-{\theta^T}{{x}^{(i)}}}} \right)-\left( 1-{{y}^{(i)}} \right)\log \left( 1+{{e}^{{\theta^T}{{x}^{(i)}}}} \right)
= − y ( i ) log ( 1 + e − θ T x ( i ) ) − ( 1 − y ( i ) ) log ( 1 + e θ T x ( i ) )
所以:
∂
∂
θ
j
J
(
θ
)
=
∂
∂
θ
j
[
−
1
m
∑
i
=
1
m
[
−
y
(
i
)
log
(
1
+
e
−
θ
T
x
(
i
)
)
−
(
1
−
y
(
i
)
)
log
(
1
+
e
θ
T
x
(
i
)
)
]
]
\frac{\partial }{\partial {\theta_{j}}}J\left( \theta \right)=\frac{\partial }{\partial {\theta_{j}}}[-\frac{1}{m}\sum\limits_{i=1}^{m}{[-{{y}^{(i)}}\log \left( 1+{{e}^{-{\theta^{T}}{{x}^{(i)}}}} \right)-\left( 1-{{y}^{(i)}} \right)\log \left( 1+{{e}^{{\theta^{T}}{{x}^{(i)}}}} \right)]}]
∂ θ j ∂ J ( θ ) = ∂ θ j ∂ [ − m 1 i = 1 ∑ m [ − y ( i ) log ( 1 + e − θ T x ( i ) ) − ( 1 − y ( i ) ) log ( 1 + e θ T x ( i ) ) ] ]
=
−
1
m
∑
i
=
1
m
[
−
y
(
i
)
−
x
j
(
i
)
e
−
θ
T
x
(
i
)
1
+
e
−
θ
T
x
(
i
)
−
(
1
−
y
(
i
)
)
x
j
(
i
)
e
θ
T
x
(
i
)
1
+
e
θ
T
x
(
i
)
]
=-\frac{1}{m}\sum\limits_{i=1}^{m}{[-{{y}^{(i)}}\frac{-x_{j}^{(i)}{{e}^{-{\theta^{T}}{{x}^{(i)}}}}}{1+{{e}^{-{\theta^{T}}{{x}^{(i)}}}}}-\left( 1-{{y}^{(i)}} \right)\frac{x_j^{(i)}{{e}^{{\theta^T}{{x}^{(i)}}}}}{1+{{e}^{{\theta^T}{{x}^{(i)}}}}}}]
= − m 1 i = 1 ∑ m [ − y ( i ) 1 + e − θ T x ( i ) − x j ( i ) e − θ T x ( i ) − ( 1 − y ( i ) ) 1 + e θ T x ( i ) x j ( i ) e θ T x ( i ) ]
=
−
1
m
∑
i
=
1
m
y
(
i
)
x
j
(
i
)
1
+
e
θ
T
x
(
i
)
−
(
1
−
y
(
i
)
)
x
j
(
i
)
e
θ
T
x
(
i
)
1
+
e
θ
T
x
(
i
)
]
=-\frac{1}{m}\sum\limits_{i=1}^{m}{{y}^{(i)}}\frac{x_j^{(i)}}{1+{{e}^{{\theta^T}{{x}^{(i)}}}}}-\left( 1-{{y}^{(i)}} \right)\frac{x_j^{(i)}{{e}^{{\theta^T}{{x}^{(i)}}}}}{1+{{e}^{{\theta^T}{{x}^{(i)}}}}}]
= − m 1 i = 1 ∑ m y ( i ) 1 + e θ T x ( i ) x j ( i ) − ( 1 − y ( i ) ) 1 + e θ T x ( i ) x j ( i ) e θ T x ( i ) ]
=
−
1
m
∑
i
=
1
m
y
(
i
)
x
j
(
i
)
−
x
j
(
i
)
e
θ
T
x
(
i
)
+
y
(
i
)
x
j
(
i
)
e
θ
T
x
(
i
)
1
+
e
θ
T
x
(
i
)
=-\frac{1}{m}\sum\limits_{i=1}^{m}{\frac{{{y}^{(i)}}x_j^{(i)}-x_j^{(i)}{{e}^{{\theta^T}{{x}^{(i)}}}}+{{y}^{(i)}}x_j^{(i)}{{e}^{{\theta^T}{{x}^{(i)}}}}}{1+{{e}^{{\theta^T}{{x}^{(i)}}}}}}
= − m 1 i = 1 ∑ m 1 + e θ T x ( i ) y ( i ) x j ( i ) − x j ( i ) e θ T x ( i ) + y ( i ) x j ( i ) e θ T x ( i )
=
−
1
m
∑
i
=
1
m
y
(
i
)
(
1
+
e
θ
T
x
(
i
)
)
−
e
θ
T
x
(
i
)
1
+
e
θ
T
x
(
i
)
x
j
(
i
)
=-\frac{1}{m}\sum\limits_{i=1}^{m}{\frac{{{y}^{(i)}}\left( 1\text{+}{{e}^{{\theta^T}{{x}^{(i)}}}} \right)-{{e}^{{\theta^T}{{x}^{(i)}}}}}{1+{{e}^{{\theta^T}{{x}^{(i)}}}}}x_j^{(i)}}
= − m 1 i = 1 ∑ m 1 + e θ T x ( i ) y ( i ) ( 1 + e θ T x ( i ) ) − e θ T x ( i ) x j ( i )
=
−
1
m
∑
i
=
1
m
(
y
(
i
)
−
e
θ
T
x
(
i
)
1
+
e
θ
T
x
(
i
)
)
x
j
(
i
)
=-\frac{1}{m}\sum\limits_{i=1}^{m}{({{y}^{(i)}}-\frac{{{e}^{{\theta^T}{{x}^{(i)}}}}}{1+{{e}^{{\theta^T}{{x}^{(i)}}}}})x_j^{(i)}}
= − m 1 i = 1 ∑ m ( y ( i ) − 1 + e θ T x ( i ) e θ T x ( i ) ) x j ( i )
=
−
1
m
∑
i
=
1
m
(
y
(
i
)
−
1
1
+
e
−
θ
T
x
(
i
)
)
x
j
(
i
)
=-\frac{1}{m}\sum\limits_{i=1}^{m}{({{y}^{(i)}}-\frac{1}{1+{{e}^{-{\theta^T}{{x}^{(i)}}}}})x_j^{(i)}}
= − m 1 i = 1 ∑ m ( y ( i ) − 1 + e − θ T x ( i ) 1 ) x j ( i )
=
−
1
m
∑
i
=
1
m
[
y
(
i
)
−
h
θ
(
x
(
i
)
)
]
x
j
(
i
)
=-\frac{1}{m}\sum\limits_{i=1}^{m}{[{{y}^{(i)}}-{h_\theta}\left( {{x}^{(i)}} \right)]x_j^{(i)}}
= − m 1 i = 1 ∑ m [ y ( i ) − h θ ( x ( i ) ) ] x j ( i )
=
1
m
∑
i
=
1
m
[
h
θ
(
x
(
i
)
)
−
y
(
i
)
]
x
j
(
i
)
=\frac{1}{m}\sum\limits_{i=1}^{m}{[{h_\theta}\left( {{x}^{(i)}} \right)-{{y}^{(i)}}]x_j^{(i)}}
= m 1 i = 1 ∑ m [ h θ ( x ( i ) ) − y ( i ) ] x j ( i )
C
o
s
t
(
h
θ
(
x
(
i
)
,
y
(
i
)
)
=
=
{
−
l
g
(
h
θ
(
x
)
)
i
f
y
=
1
−
l
g
(
1
−
h
θ
(
x
)
)
i
f
y
=
0
Cost(h_\theta(x^{(i)},y^{(i)})==\begin{cases}-lg(h_\theta(x))&if&y=1 \\-lg(1-h_\theta(x))&if&y=0\end{cases}
C o s t ( h θ ( x ( i ) , y ( i ) ) = = { − l g ( h θ ( x ) ) − l g ( 1 − h θ ( x ) ) i f i f y = 1 y = 0
h
θ
(
x
)
{h_\theta}\left( x \right)
h θ ( x )
C
o
s
t
(
h
θ
(
x
)
,
y
)
Cost\left( {h_\theta}\left( x \right),y \right)
C o s t ( h θ ( x ) , y )
这样构建的
C
o
s
t
(
h
θ
(
x
)
,
y
)
Cost\left( {h_\theta}\left( x \right),y \right)
C o s t ( h θ ( x ) , y )
y
=
1
y=1
y = 1
h
θ
(
x
)
{h_\theta}\left( x \right)
h θ ( x )
y
=
1
y=1
y = 1
h
θ
(
x
)
{h_\theta}\left( x \right)
h θ ( x )
h
θ
(
x
)
{h_\theta}\left( x \right)
h θ ( x )
y
=
0
y=0
y = 0
h
θ
(
x
)
{h_\theta}\left( x \right)
h θ ( x )
y
=
0
y=0
y = 0
h
θ
(
x
)
{h_\theta}\left( x \right)
h θ ( x )
h
θ
(
x
)
{h_\theta}\left( x \right)
h θ ( x )
Python 代码实现:
import numpy as np
def cost ( theta, X, y) :
theta = np. matrix( theta)
X = np. matrix( X)
y = np. matrix( y)
first = np. multiply( - y, np. log( X* theta. T) )
second = np. multiply( ( 1 - y) , np. log( 1 - X* theta. T) )
return np. sum ( first - second) / ( len ( X) )
Logistic regression cost function:
KaTeX parse error: Got function '\sum' with no arguments as argument to '\underset' at position 61: …{\underset{i=1}\̲s̲u̲m̲}Cost(h_\theta(…
这个式子可以合并成:
C
o
s
t
(
h
θ
(
x
)
,
y
)
=
−
y
×
l
o
g
(
h
θ
(
x
)
)
−
(
1
−
y
)
×
l
o
g
(
1
−
h
θ
(
x
)
)
Cost\left( {h_\theta}\left( x \right),y \right)=-y\times log\left( {h_\theta}\left( x \right) \right)-(1-y)\times log\left( 1-{h_\theta}\left( x \right) \right)
C o s t ( h θ ( x ) , y ) = − y × l o g ( h θ ( x ) ) − ( 1 − y ) × l o g ( 1 − h θ ( x ) )
C
o
s
t
(
h
θ
(
x
)
,
y
)
=
−
y
×
l
o
g
(
h
θ
(
x
)
)
−
(
1
−
y
)
×
l
o
g
(
1
−
h
θ
(
x
)
)
Cost\left( {h_\theta}\left( x \right),y \right)=-y\times log\left( {h_\theta}\left( x \right) \right)-(1-y)\times log\left( 1-{h_\theta}\left( x \right) \right)
C o s t ( h θ ( x ) , y ) = − y × l o g ( h θ ( x ) ) − ( 1 − y ) × l o g ( 1 − h θ ( x ) )
=
−
1
m
∑
i
=
1
m
[
y
(
i
)
log
(
h
θ
(
x
(
i
)
)
)
+
(
1
−
y
(
i
)
)
log
(
1
−
h
θ
(
x
(
i
)
)
)
]
=-\frac{1}{m}\sum\limits_{i=1}^{m}{[{{y}^{(i)}}\log \left( {h_\theta}\left( {{x}^{(i)}} \right) \right)+\left( 1-{{y}^{(i)}} \right)\log \left( 1-{h_\theta}\left( {{x}^{(i)}} \right) \right)]}
= − m 1 i = 1 ∑ m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ]
我们要求出
min
J
(
θ
)
\min J(\theta)
min J ( θ )
,
另
外
,
我
们
假
设
的
输
出
,
实
际
上
就
是
这
个
概
率
值
:
,另外,我们假设的输出,实际上就是这个概率值:
, 另 外 , 我 们 假 设 的 输 出 , 实 际 上 就 是 这 个 概 率 值 :
x
x
x
为
参
数
,
为参数,
为 参 数 ,
y
=
1
y=1
y = 1
我们要使
min
J
(
θ
)
\min J(\theta)
min J ( θ )
θ
j
:
=
θ
j
−
α
1
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
{\theta_j}:={\theta_j}-\alpha \frac{1}{m}\sum\limits_{i=1}^{m}{({h_\theta}({{x}^{(i)}})-{{y}^{(i)}}){x_{j}}^{(i)}}
θ j : = θ j − α m 1 i = 1 ∑ m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i )
其中这个和线性回归的梯度下降在形式上一致,但是假设却是不一致的,其中线性回归的假设函数是
h
θ
(
x
)
=
θ
T
X
=
θ
0
x
0
+
θ
1
x
1
+
θ
2
x
2
+
.
.
.
+
θ
n
x
n
{h_\theta}\left( x \right)={\theta^T}X={\theta_{0}}{x_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+...+{\theta_{n}}{x_{n}}
h θ ( x ) = θ T X = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n
h
θ
=
1
1
+
e
−
θ
T
X
h_\theta=\frac{1}{1+e^{-\theta^TX}}
h θ = 1 + e − θ T X 1
当使用梯度下降法来实现逻辑回归时,我们有这些不同的参数$\theta
,
就
是
,就是
, 就 是
θ
1
{\theta_{1}}
θ 1
θ
2
{\theta_{2}}
θ 2
θ
n
{\theta_{n}}
θ n for循环 来更新这些参数值,理想情况下,我们更提倡使用向量化的实现,可以把所有这些
n
n
n
octave。。。
在上面中,我们讨论的是二分类问题,当多分类问题时,怎么办呢?
我们可以在多分类中提取一个类,并作为正类,其余作为负类。进行逻辑回归,由此可以把与其他类区分出来,所以对各个类操作可以把所有的类区分开来。
为了能实现这样的转变,我们将多个类中的一个类标记为正向类(
y
=
1
y=1
y = 1
h
θ
(
1
)
(
x
)
h_\theta^{\left( 1 \right)}\left( x \right)
h θ ( 1 ) ( x )
y
=
2
y=2
y = 2
h
θ
(
2
)
(
x
)
h_\theta^{\left( 2 \right)}\left( x \right)
h θ ( 2 ) ( x )
h
θ
(
i
)
(
x
)
=
p
(
y
=
i
∣
x
;
θ
)
h_\theta^{\left( i \right)}\left( x \right)=p\left( y=i|x;\theta \right)
h θ ( i ) ( x ) = p ( y = i ∣ x ; θ )
i
=
(
1
,
2
,
3....
k
)
i=\left( 1,2,3....k \right)
i = ( 1 , 2 , 3 . . . . k )
最后,在我们需要做预测时,我们将所有的分类机都运行一遍,然后对每一个输入变量,都选择最高可能性的输出变量。
总之,我们已经把要做的做完了,现在要做的就是训练这个逻辑回归分类器:
h
θ
(
i
)
(
x
)
h_\theta^{\left( i \right)}\left( x \right)
h θ ( i ) ( x )
i
i
i
y
=
i
y=i
y = i
x
x
x
x
x
x
h
θ
(
i
)
(
x
)
h_\theta^{\left( i \right)}\left( x \right)
h θ ( i ) ( x )
,
即
,即
, 即



![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QP9Fv0PO-1581090656051)(https://img.vim-cn.com/84/3fb0dbd3fc2144ee394f5447dfe10f220e5423.png)]](https://img-blog.csdnimg.cn/20200207235231630.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-D7fwLZyd-1581090656052)(https://img.vim-cn.com/eb/19287d43de640d859224a2c83f6fa6403483ba.png)]](https://img-blog.csdnimg.cn/2020020723525369.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7B8YFPvX-1581090656054)(https://img.vim-cn.com/77/7e96f7e199a6212699947a2974ecfe7ba2f25e.png)]](https://img-blog.csdnimg.cn/20200207235421997.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jfC2OsjK-1581090656055)(https://img.vim-cn.com/dd/414020abe286b46d33b2b86ac655f0fdb57240.png)]](https://img-blog.csdnimg.cn/20200207235452741.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQzMzA5Mjg2,size_16,color_FFFFFF,t_70)
