最短路径算法

Floyd-Warshall（弗洛伊德算法）

弗洛伊德算法的原理是动态规划，用于计算两点之间的最短路径。该算法的优点在于极其简单，代码仅几行。缺点是时间复杂度高O(n^{3)，空间复杂度Ω(n}2)

算法描述

算法用于比较图结构中两个顶点间所有可能的路径。点集合设为V(1…k)，求点i，点j中间经过k的最短距离D(i,j,k)

最短路径经过点k。D(i,j,k)=D(i,k,k-1)+D(k,j,k-1)。此时中间点集合V(1…k-1)
最短路径不经过点k。D(i,j,k)=D(i,j,k-1)。此时中间点集合V(1…k-1)

代码实现

public class FloydWarshall {

    public static void shortestPath(int[][] originWeight) {
        int[][] shortestWeight = new int[originWeight.length][originWeight.length];
        for (int i = 0; i < originWeight.length; i++) {
            for (int j = 0; j < originWeight.length; j++) {
                // 如果不经过k点的最短路径
                shortestWeight[i][j] = originWeight[i][j];
                for (int k = 0; k < originWeight.length; k++) {
                    int edgeWeightStartMiddle = originWeight[i][k];
                    int edgeWeightMiddleEnd = originWeight[k][j];
                    // 发现经过k点的最短路径比不经过k点的最短路径更短。更新最短路径
                    if (shortestWeight[i][j] > edgeWeightStartMiddle + edgeWeightMiddleEnd) {
                        shortestWeight[i][j] = edgeWeightStartMiddle + edgeWeightMiddleEnd;
                        System.out.print(String.format("点%s与点%s之间最小权重路径插入点%s;", i, j, k));
                    }
                }
                System.out.println(String.format("点%s与点%s之间最小权重为：%s", i, j, shortestWeight[i][j]));
            }
        }
    }

    /**
     * 初始化构建图（邻接矩阵形式）
     * @param size : 矩阵大小
     */
    public static int[][] init(int size){
        int[][] originWeight = new int[size][size];
        Random random = new Random();
        for (int i = 0; i < size; i++) {
            for (int j = 0; j < size; j++) {
                // 点i至点j这条边的权重（路径长度）
                originWeight[i][j] = random.nextInt(size * size);
            }
        }
        return originWeight;
    }

    public static void main(String[] args) {
        int[][] matrixGraph = init(4);
        PrintUtil.print2DimensionArray(matrixGraph);
        shortestPath(matrixGraph);
    }

}

执行结果

[(0-0:8),(0-1:8),(0-2:13),(0-3:13),(1-0:14),(1-1:15),(1-2:8),(1-3:5),(2-0:15),(2-1:7),(2-2:9),(2-3:3),(3-0:5),(3-1:1),(3-2:2),(3-3:1),]

点0与点0之间最小权重为：8
点0与点1之间最小权重为：8
点0与点2之间最小权重为：13
点0与点3之间最小权重为：13
点1与点0之间最小权重路径插入点3;点1与点0之间最小权重为：10
点1与点1之间最小权重路径插入点3;点1与点1之间最小权重为：6
点1与点2之间最小权重路径插入点3;点1与点2之间最小权重为：7
点1与点3之间最小权重为：5
点2与点0之间最小权重路径插入点3;点2与点0之间最小权重为：8
点2与点1之间最小权重路径插入点3;点2与点1之间最小权重为：4
点2与点2之间最小权重路径插入点3;点2与点2之间最小权重为：5
点2与点3之间最小权重为：3
点3与点0之间最小权重为：5
点3与点1之间最小权重为：1
点3与点2之间最小权重为：2
点3与点3之间最小权重为：1
Process finished with exit code 0

Dijkstra（迪克斯特拉算法）

算法描述

原理：戴克斯特拉算法（也叫迪克斯特拉算法）使用了广度优先搜索解决赋权有向图的单源最短路径问题。
算法版本：戴克斯特拉的原始版本是找到两个顶点之间的最短路径，但是更常见的变体固定了一个顶点作为源节点然后找到该顶点到图中所有其它节点的最短路径，产生一个最短路径树
复杂度：最初的戴克斯特拉算法不采用最小优先级队列，时间复杂度是O(V^2)(其中V为图的顶点个数)。通过斐波那契堆实现的戴克斯特拉算法时间复杂度是O(E+V*log(V)) (其中E是边数) 。对于不含负权的有向图，这是目前已知的最快的单源最短路径算法
在这里插入图片描述

代码实现

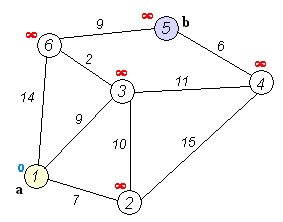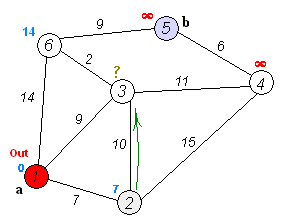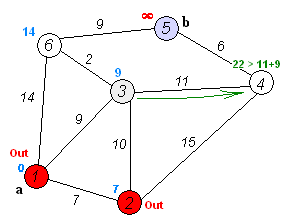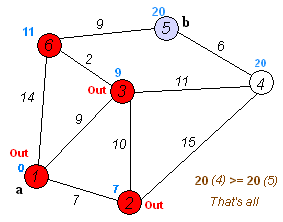
图片来源于网络：https://zh.wikipedia.org/wiki/File:Dijkstra_Animation.gif
所有顶点的边
顶点1：1->2,1->3,1->6
顶点2：2->3,2->4
顶点3：3->6,3->4
顶点4：4->5
顶点5：无
顶点6：6->5
在这里插入图片描述

package org.gallant.shortest.path;

import com.google.common.collect.Lists;
import java.util.List;
import java.util.PriorityQueue;
import lombok.Builder;
import lombok.Data;

/**
 * @author 会灰翔的灰机
 * @date 2020/2/12
 */
public class DijkstraWithPriorityQueue {

    /**
     * 起点到终点的最短路径
     * start，end分别为点的下标
     */
    public static void shortestPath(List<List<Node>> graph, int start, int end) {
        List<Node> allPathStarts = graph.get(start);
        if (allPathStarts != null && allPathStarts.size() > 0) {
            int leastWeight = Integer.MAX_VALUE;
            for (int i = 0; i < allPathStarts.size(); i++) {
                List<Integer> currentPath = Lists.newArrayList(start);
                int pathLeastWeight = shortestPathRelaxation(graph, allPathStarts.get(i), end, currentPath);
                System.out.println(currentPath);
                if (pathLeastWeight < leastWeight) {
                    leastWeight = pathLeastWeight;
                }
            }
            System.out.println("leastWeight:"+leastWeight);
        }
    }

    public static int shortestPathRelaxation(List<List<Node>> graph, Node startNode, int end, List<Integer> currentPath) {
        int leastWeight = startNode.weight;
        currentPath.add(startNode.num);
        if (startNode.num == end) {
            return startNode.weight;
        }
        List<Node> allPathStarts = graph.get(startNode.num);
        if (allPathStarts != null && allPathStarts.size() > 0) {
            PriorityQueue<Node> priorityQueue = new PriorityQueue<>(allPathStarts);
            Node leastWeightNode = priorityQueue.poll();
            if (leastWeightNode != null) {
                leastWeight += shortestPathRelaxation(graph, leastWeightNode, end, currentPath);
            }
        }
        return leastWeight;
    }

    /**
     * 初始化构建图（邻接链表形式）
     */
    public static List<List<Node>> init(){
        List<List<Node>> originWeight = Lists.newArrayList();
        for (int i = 0; i < 7; i++) {
            originWeight.add(Lists.newArrayList());
        }
        originWeight.get(1).addAll(Lists.newArrayList(
                Node.builder().num(2).weight(7).build(), Node.builder().num(3).weight(9).build(), Node
                        .builder().num(6).weight(14).build()));
        originWeight.get(2).addAll(Lists.newArrayList(
                Node.builder().num(3).weight(10).build(), Node.builder().num(4).weight(15).build()));
        originWeight.get(3).addAll(Lists.newArrayList(
                Node.builder().num(6).weight(2).build(), Node.builder().num(4).weight(11).build()));
        originWeight.get(4).addAll(Lists.newArrayList(Node.builder().num(5).weight(6).build()));
        originWeight.get(6).addAll(Lists.newArrayList(Node.builder().num(5).weight(9).build()));
        return originWeight;
    }

    public static void main(String[] args) {
        List<List<Node>> listGraph = init();
        System.out.println(listGraph);
        shortestPath(listGraph, 1, 5);
    }

    @Data
    @Builder
    private static class Node implements Comparable<Node> {
        private Integer num;
        private Integer weight;

        @Override
        public int compareTo(Node o) {
            return weight - o.weight;
        }
    }

}

Bellman–Ford（贝尔曼-福特）

算法描述

它的原理是对图进行次松弛(迭代法)操作与迪克斯特拉算法类似，区别在于它将邻接链表节点的每一种可能均做了计算，得到所有可能的最短路径，所以复杂度更高。O(V^2)，V为顶点个数。其优于迪克斯特拉算法的方面是边的权值可以为负数、实现简单，缺点是时间复杂度过高。但算法可以进行若干种优化，提高效率。
在这里插入图片描述

代码实现

代码实现依然按照迪克斯特拉案例中的gif图的结构实现

package org.gallant.shortest.path;

import com.google.common.collect.Lists;
import java.util.List;
import lombok.Builder;
import lombok.Data;

/**
 * @author 会灰翔的灰机
 * @date 2020/2/12
 */
public class BellmanFord {

    /**
     * 起点到终点的最短路径
     * start，end分别为点的下标
     * 目前是一个顶点至另一个顶点的场景，复杂度为1*边数，计算所有顶点复杂度则为：（顶点数-1）*边数
     */
    public static void shortestPath(List<List<Node>> graph, int start, int end, int currentWeight, List<Integer> currentPath) {
        currentPath.add(start);
        if (start == end) {
            System.out.println(currentPath+"="+currentWeight);
        }
        // 取出顶点的所有边
        List<Node> allPathStarts = graph.get(start);
        if (allPathStarts != null && allPathStarts.size() > 0) {
            // 遍历每个顶点计算所有可能路径的最小代价
            for (int i = 0; i < allPathStarts.size(); i++) {
                shortestPath(graph, allPathStarts.get(i).num, end, allPathStarts.get(i).weight + currentWeight, Lists.newArrayList(currentPath));
            }
        }
    }

    /**
     * 初始化构建图（邻接链表形式）
     */
    public static List<List<Node>> init(){
        List<List<Node>> originWeight = Lists.newArrayList();
        for (int i = 0; i < 7; i++) {
            originWeight.add(Lists.newArrayList());
        }
        originWeight.get(1).addAll(Lists.newArrayList(Node.builder().num(2).weight(7).build(), Node.builder().num(3).weight(9).build(), Node.builder().num(6).weight(14).build()));
        originWeight.get(2).addAll(Lists.newArrayList(Node.builder().num(3).weight(10).build(), Node.builder().num(4).weight(15).build()));
        originWeight.get(3).addAll(Lists.newArrayList(Node.builder().num(6).weight(2).build(), Node.builder().num(4).weight(11).build()));
        originWeight.get(4).addAll(Lists.newArrayList(Node.builder().num(5).weight(6).build()));
        originWeight.get(6).addAll(Lists.newArrayList(Node.builder().num(5).weight(9).build()));
        return originWeight;
    }

    public static void main(String[] args) {
        List<List<Node>> listGraph = init();
        System.out.println(listGraph);
        shortestPath(listGraph, 1, 5, 0, Lists.newArrayList());
    }

    @Data
    @Builder
    private static class Node {
        private Integer num;
        private Integer weight;
    }

}

执行结果

[[], [Dijkstra.Node(num=2, weight=7), Dijkstra.Node(num=3, weight=9), Dijkstra.Node(num=6, weight=14)], [Dijkstra.Node(num=3, weight=10), Dijkstra.Node(num=4, weight=15)], [Dijkstra.Node(num=6, weight=2), Dijkstra.Node(num=4, weight=11)], [Dijkstra.Node(num=5, weight=6)], [], [Dijkstra.Node(num=5, weight=9)]]
[1, 2, 3, 6, 5]=28
[1, 2, 3, 4, 5]=34
[1, 2, 4, 5]=28
[1, 3, 6, 5]=20
[1, 3, 4, 5]=26
[1, 6, 5]=23
显然最短路径是20，对应的路径为：1->3->6->5

SPFA（Shortest Path Faster Algorithm）

算法描述

对于Bellman-Ford算法的队列优化算法
SPFA 最坏情况下复杂度和朴素 Bellman-Ford 相同，为 O(VE)。V：顶点，E：边

代码实现

同Dijkstra实现，原理是对于Bellman-Ford算法增加一个优先级队列减少冗余计算。
一个基于欧氏几何距离的SPFA算法。红线是当前状态下的各条最短路径。蓝线表示松弛发生的地方。下图取自：https://zh.wikipedia.org/zh-hans/%E6%9C%80%E7%9F%AD%E8%B7%AF%E5%BE%84%E5%BF%AB%E9%80%9F%E7%AE%97%E6%B3%95
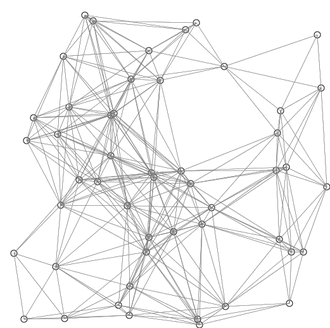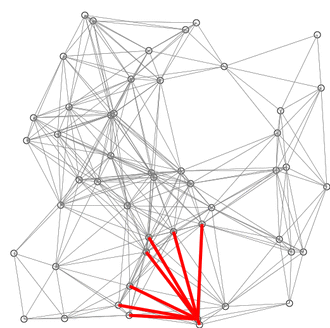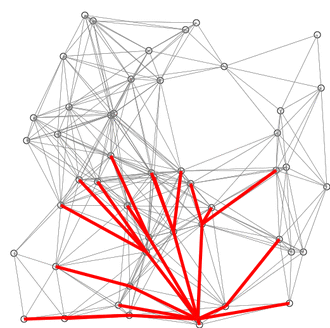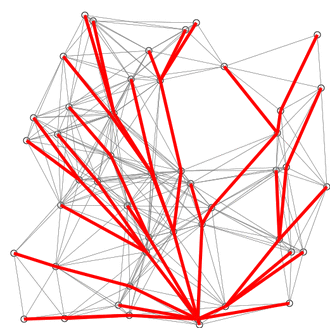
在这里插入图片描述

总结

Floyd-Warshall算法实现可以说是最为简单，可以解决负权边问题。
Dijkstra算法实现较复杂，时间复杂度低，不能解决负权边问题。但是博客中给出的实现方式解决了负权问题。
Bellman算法时间较复杂，变形很多，时间复杂度较高但是可以通过各种方式优化。可以解决负权边问题。

负权边问题的常见应用解决金额类问题。金额有收入支出正负之分。
正权边问题的常见应用解决路径类问题

会灰翔的灰机

发布了91 篇原创文章 · 获赞 103 · 访问量 3万+

私信关注

Floyd-Warshall、Dijkstra、Bellman–Ford、SPFA

Floyd-Warshall（弗洛伊德算法）

算法描述

代码实现

执行结果

Dijkstra（迪克斯特拉算法）

算法描述

代码实现

Bellman–Ford（贝尔曼-福特）

算法描述

代码实现

执行结果

SPFA（Shortest Path Faster Algorithm）

算法描述

代码实现

总结

猜你喜欢