本篇介绍的LL(1)分析,这是一种自上而下分析的方法,第一个 L 表示从左向右扫描,
第二个 L 表示分析过程是最左推导,(1)表示每次只向前看一个符号进行分析
关于语法描述的概念
本文中,若无特别说明,小写字母[a-z]表示终结符,α、β等∈(VT∪VN)*,ABCD等表示非终结符
自上而下分析
- 从文法的开始符号出发,向下推导。推出句子
- 根据输入串,从文法开始符号(根结点)出发,自上而下地为输入串建立语法树
eg:
有语法:S → xAy A → ** | *
从左向右扫描输入串,取到 x 进行匹配时,分析文法开始符号 S 的产生式,只有一个 S → xAy,
那么只能将 S 推导为句型 xAy,继续由 xAy 来匹配输入串,
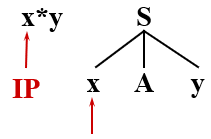
输入符号(终结符)x 与 当前句型中的 x 相匹配,则继续用 Ay 匹配剩下的输入串 *y
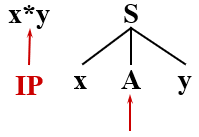
对符号 * 进行匹配,遇到非终结符 A,分析 A 可进行的推导,A → ** | *
按照先后顺序,先尝试 A → **,则现在的的分析树变成
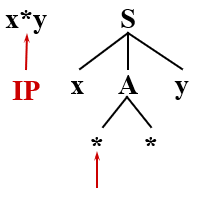
很好,我们使 * 得到了匹配,继续匹配
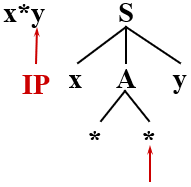
哟吼,完蛋,非终结符 * 是无法匹配 y 的,匹配失败
但是我们还有另外一条路 A → * 没试呢
回到刚刚 A 没有展开,* 等待匹配的状态,将 A 推导为 *
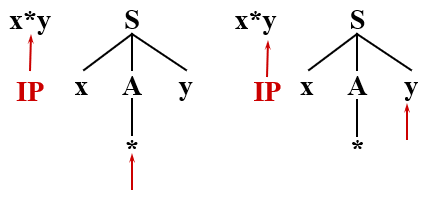
* 得到匹配后,y 也匹配成功,输入串结束且匹配成功,语法分析结束
这就是LL(1)的推导过程
那么,这种匹配方式就存在一些限制
回溯问题
这是一个非终结符具有多个产生式候选带来的问题
当一个非终结符用某个候选式进行匹配时,匹配成功可能是暂时的
如果要遍历所有匹配的可能,在每个多候选式终结符进行匹配时,就要记录下当前等待匹配
的符号的位置、当前推导句型中非终结符的位置,和该非终结符选择的产生式的序号
某次匹配失败后,舍弃某些分析结果,回溯到上一个岔路口,走下一条路尝试
回溯会导致语法分析的效率问题,
此外,最终分析失败时,没法确定应该在哪个岔路口抛出错误
还有一个上述推导示例没有反映出来的死循环问题
文法左递归问题
假设有文法:S → xAy A → A* | *
非终结符 A 的产生式是以 A 开头的串,称为左递归
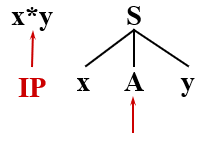
在上述匹配过程中,就会进入到 A 的左递归的产生式的无限循环中,连回溯的机会都莫得
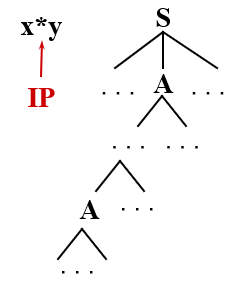
因此要消除文法的左递归,并避免回溯
消除左递归
存在左递归 P → Pα1 | Pα2 |…| Pαm | β1 |…| βn
(每个α都不等于ε,每个β都不以P开头)
观察上式,易知 P 推导出的句型为 (β1 |…| βn)(α1 | α2 |…| αm)*
通过以下方法将左递归转化为右递归(易知右递归不会进入无限循环)
P → (β1 |…| βn)P/
P/ → α1P/ | α2P/ |…| αmP/ | ε
例,有如下文法G(E):
E → E + T | T
T → T * F | F
F → (E) | i
消除左递归后
E → TE/
E/ → + TE/ | ε
T → FT/
T/ → * FT/ | ε
F → (E) | i
但是有一种特殊的左递归需要注意
S → Qc | c
Q → Rb | b
R → Sa | a
看起来没有显式的左递归,实际上暗藏玄机
S → Qc | c ⇒ S → Rbc | bc | c ⇒ S → Sabc | abc | bc | c,实际上 S、Q、R 都是左递归的
显然这种间接的左递归也需要消除
下面给出一种左递归消除算法,使用这个算法的前提条件如下:
- 不含以 ε 为右部的产生式
- 不含有回路 (非终结符 P 经一次或若干次推导再次得到 P)
实际上,这两个条件并不苛刻,大多数文法都可以满足
将文法 G 当前所有的非终结符按某种顺序排列 P1,P2,P3,……,Pn;
并按此顺序将 Pi 改造成 Pi → a | Pi+1 | Pi+2 | … | Pn ,具体做法是{
将所有的 Pi → Pjγ 的规则改写成 Pi → ( δ1 | δ2 | … | δn )γ ,其中 j < i,且 Pj → δ1 | δ2 | … | δn
然后消除 Pi 里的直接左递归,得到形如 Pi → a | Pi+1 | Pi+2 | … | Pn 的 Pi
}
消除左递归后的文法规则中可能有一些无法到达,删除它们
另外,由于初始排列顺序的不同,最终消除左递归后的得到的文法规则可能不同,但是它们产生的语言是一样的(证明略)
消除回溯
消除回溯即是要保证,匹配某个符号时,可选择的候选式是唯一的、准确的,
若输入串是合法的句子,所选推导一定可以使输入串分析成功;如果分析不成功,则输入串一定不是合法句子
那么在匹配符号 a 时,非终结符 P 仅有一个产生式可以推导出以 a 开头的串,就是我们需要的情况
FIRST集合
由上面的想法,对不含左递归的文法 G 所有非终结符的每个候选 α 定义终结首符集FIRST集合如下
FIRST(α) = { a | α ⇒* a…,a ∈ VT },即FIRST(α)中的符号均是候选 α 可以推导出的串的第一个终结符
特别是,若 α ⇒* ε,规定 ε ∈ FIRST(α)
那么上述想法用FIRST集合的概念描述就是
非终结符 A 的任何两个不同的候选 αi、αj,有FIRST(αi) ∩ FIRST(αj) = ∅
当使用 A 去匹配输入符号 a 时,若某FIRST(α)中包含a,就选择 A 的候选式 α
斯巴拉西,但是如何保证 FIRST(αi) ∩ FIRST(αj) = ∅ 呢?
有提取左公共因子算法如下
若关于 A 的语法规则符合如下形式:A → δβ1 | δβ2 | … | δβn | δ | γ1 | γ2 | … | γm
则提取左公因子 A → δA/ | γ1 | γ2 | … | γm,A/ → β1 | β2 | … | βn | ε |
继续检查 A 与 A/ 的候选式是否可以继续提取
反复提取左公共因子(包括新引入的非终结符),就可以使得所有候选首符集两两不相交
现在我们已经得到不含有左递归、对于任何输入符号都能确定唯一推导过程的文法
然而,还是有一种情形会使我们的推导有不确定性
考虑如下文法
S → AB
A → a | ε
B → aC
C → ……
当匹配输入串 ab…… 时,取到输入符号 a,将 S 推导为 AB 后,
出现了无法确定推导过程的情形:
- 将 A 推导为 a ,a 匹配成功,进行下一单词的匹配
- 将 A 推导为 ε,用 B 去匹配 a ,再继续进行推导
注意我们是无回溯的,当然不能有岔路
FOLLOW集合
为了确定化这种情况(FOLLOW集合的作用:判断能不能将非终结符推导为 ε ),定义FOLLOW集如下
FOLLOW(A) = { a | S ⇒*…Aa…,a ∈ VT },有些输入串以 # 作为结束标志,因此若 S ⇒*…A,规定 # ∈ FOLLOW(A)
若某个非终结符 A 的候选首符集FIRST(αi)包含 ε,则要求FIRST(αi)∩FOLLOW(A) = ∅
也就是说,如果某个等待匹配的输入符号 a,不属于此时的非终结符 A 的FIRST集合,就会有三种情况
- A 的候选首符集均不包含 ε,a 匹配失败,a 此时在输入串中导致语法错误
- A 的某个候选首符集包含 ε,且 a ∈ FOLLOW(A),则将 A 推导为 ε,继续由 A 后的推导串来匹配 a
- A 的某个候选首符集包含 ε,且 a ∉ FOLLOW(A),a 匹配失败,a 此时在输入串导中致语法错误
okk,罗里吧嗦这么多,终于把适用于LL(1)分析的文法的限制条件讲完辽
再总结一遍
- 文法不含左递归
- 文法中每一个非终结符 A 的各个产生式的候选首符集不相交,即若 A → α1 | α2 | … | αn
FIRST(αi)∩FIRST(αj) = ∅,i ≠ j - 对于文法中的每个非终结符 A,若它的某个候选首符集包含 ε,则 FIRST(αi)∩FOLLOW(A) = ∅
一个文法,先消除左递归,再提取公共左因子,得到的文法 G 若满足以上条件,
则称文法 G 为LL(1)文法,可以进行LL(1)分析
LL(1)分析的过程如下:
假设当前等待匹配的符号为 a,进行匹配的非终结符为A,A 的所有产生式为 A → α1 | α2 | … | αn,
- 若 a ∈ FIRST(αi),则将 A 推导为 αi,a得到匹配,斯巴拉西,继续分析下一个符号 ①
- 若 a ∉ FIRST(αi)
- 若 ε ∈ FIRST(αi),且 a ∈ FOLLOW(A),则将 A 推导为 ε,a 交给 A 后面的串匹配 ②
- 否则,匹配失败,a 此时在输入串中是语法错误 ③
如果这个文法是LL(1)文法,则每一步都能且只能在①②③中确定,每一步都只有一种情况。这就是LL(1)分析
妙呀
构造FIRST集合和FOLLOW集合
还有一个问题没有解决,判断文法是否是LL(1)文法,以及分析过程中都要用到FIRST集合和FOLLOW集合
FIRST集合
按照FIRST集合的定义,FIRST(α) = { a | α ⇒* a…,a ∈ VT }
将 α 分情况讨论
- α = X,X ∈ VT∪VN
- α = X1X2…Xn,Xi ∈ VT∪VN
通过反复扫描产生式,运用以下规则构造FIRST集合,直到每个FIRST(α)不再变化
构造每个文法符号的FIRST集合
对于每一个X∈VT∪VN,
- 若X∈VT,则FIRST(X) = { X };
- 若X∈VN,
- 若产生式形如 X → a…,则把 a 加入到FIRST(X)中;
若 X → ε 也是产生式,则把 ε 也加入到FIRST(X)中; - 若 X → Y… 是一个产生式,且 Y∈VN,则把FIRST(Y)中的所有非 ε 元素加入到FIRST(X)中;
- 若 X → Y1Y2…Yi-1Yi…Yk,Y1 ~ Yi-1 都是非终结符,
若FIRST(Y1) ~ FIRST(Yi-1)均含有 ε,即 Y1…Yi-1 ⇒* ε,则将FIRST(Yi)加入FIRST(X);
若所有 FIRST(Y) 均含有 ε,即 Y1Y2…Yi-1Yi…Yk ⇒* ε,则将 ε 加入FIRST(X);
- 若产生式形如 X → a…,则把 a 加入到FIRST(X)中;
构造任何符号串 α 的FIRST集合
对于文法 G 的任何符号串 α = X1X2…Xn 构造集合FIRST(α),
- 将FIRST(X1) - {ε} 加入FIRST(α);
- 若FISRT(X1) ~ FIRST(Xi-1)均包含 ε,则将FIRST(Xi) - {ε} 加入FIRST(α);
- 若FISRT(X1) ~ FIRST(Xn)均包含 ε,则将 ε 加入FIRST(α);
构造FOLLOW集合
首先是FOLLOW集合的定义 FOLLOW(A) = { a | S ⇒* …Aa…,a ∈ VT }
反复使用以下规则,对文法 G 的每个非终结符A构造FOLLOW(A),直至每个FOLLOW不再变化为止
- 将输入串结束标志 # 加入文法的开始符号S对应的FOLLOW(S)中
- 若 A → αBβ 是一个产生式,则把 FIRST(β) - {ε} 加入到FOLLOW(B)中
- 若 A → αB 是一个产生式,或 A → αBβ 是一个产生式而 β ⇒* ε(即 ε ∈ FIRST(β)),则把 FOLLOW(A)加入到FOLLOW(B)中
注意上述步骤中,α、β ∈ (VT ∩ VN)*,B ∈ VN
例:文法G(E)为
E → TE/
E/ → + TE/ | ε
T → FT/
T/ → * FT/ | ε
F → (E) | i
则文法 G 的FIRST集合与FOLLOW集合为
FIRST(E) = { (,i } FOLLOW(E) = { #,) }
FIRST(E/) = { +,ε } FOLLOW(E/) = { #,) }
FIRST(T) = { (,i } FOLLOW(T) = { +,#,) }
FIRST(T/) = { *,ε } FOLLOW(T/) = { +,#,) }
FIRST(F) = { (,i } FOLLOW(F) = { *,+,#,) }
消除左递归、提取公共左因子后,再构造这个文法的FIRST集合和FOLLOW集合,
判断其是否为LL(1)文法,若是,则可以使用LL(1)的分析方法进行语法分析
2019/8/10
