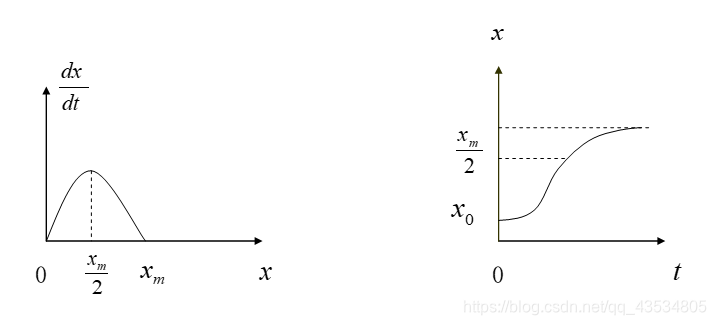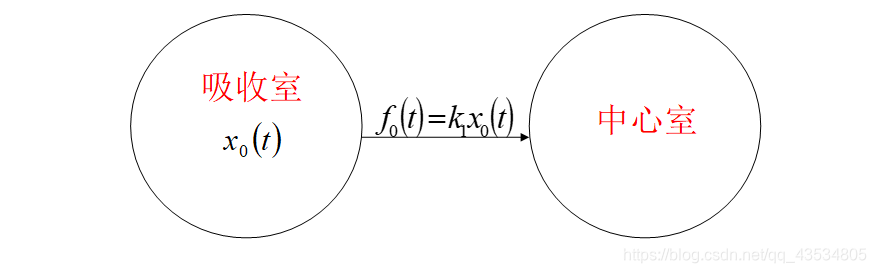第二章:微积分方法建模
overview:
涉及连续的变量,可以用微积分求解,求得解析式便于下一步分析。有些离散的变量也可以演变成连续变量进行求解。当我们描述实际对象的某些特性随时间(或空间)而演变的过程,分析它的变化规律,预测它的未来性态时,通常要建立对象的动态模型。建模时首先要根据建模目的和对问题的具体分析作出简化假设,然后按照对象内在的或可以类比的其它对象的规律列出微分方程,求出方程的解并将结果翻译回实际对象,就可以进行描述、分析或预测了。
2.1飞机降落曲线
飞机降落时,其曲线是一条三次抛物线,如下图:

水平速度为常数u,出于安全考虑,飞机的垂直加速度不得超过g/10,已知飞行高度h,要求在坐标原点降落,求开始下降点x0允许的最小值。
求曲线解析式
设飞机降落曲线为:
y=ax3+bx2+cx+d
依据假设可知:
y(0)=0,y(x0)=h,y′(0)=0,y′(x0)=0,带入上式可得:
⎩⎪⎪⎨⎪⎪⎧y(0)=d=0,y′(0)=c=0,y(x0)=ax3+bx2+cx+d=h,y′(x0)=3ax2+2bx0+c=0x=0
所以:
a=−x032h,b=x023h,c=0,d=0
其曲线为:
y=−x02h(x02x3−3x2)
求最佳着陆点
飞机垂直速度是y关于时间t的导数:
dtdy=−x02h(x06x2−6x)dtdx
其中,
dtdx是飞机水平速度,所以
dtdx=u,则:
dtdy=−x026hu(x0x2−x)
垂直加速度为:
dt2d2y=−x026hu(x02x−1)dtdx=−x026hu2(x02x−1)
设
a(x)=dt2d2y,则:
∣a(x)∣=x026hu2∣x02x−1∣,x∈[0,x0]
所以,垂直加速度最大值为:
max∣a(x)∣=x026hu2,x∈[0,x0]
由于题目限制:
max∣a(x)∣≤10g,所以:
x0≥ug60h
,此为
x0的最小值。
2.2经济增长模型
发展经济、增加生产有两个重要因素,一是增加投资(扩大厂房、购买设备、技术革新等),二是增加劳动力。恰当调节投资增长和劳动力增长的关系,使增加的产量不致被劳动力的增长抵消,劳动生产率才能不断提高,从而真正起到发展经济的作用。为此,需要分析产量、劳动力和投资之间变化规律,从而保证经济正常发展。
假设:
Q(t)——地区、部门、企业在某时间t的产量
L(t)——地区、部门、企业在某时间t的劳动力
K(t)——地区、部门、企业在某时间t的资金
Z(t)——每个劳动力在某时间t所占有的产量(劳动力生产率)
道格拉斯(Douglas)生产函数
由于我们只关心产量、劳动力、投资的相对增长,而不是绝对量,所以定义:
产量指数:
iQ(t)=Q(0)Q(t),劳动力指数:
iL(t)=L(0)L(t),投资指数:
iK(t)=K(0)K(t) (1)
令:
ξ(t)=lniK(t)iL(t),
ψ(t)=lniK(t)iQ(t) (2)
根据统计数据,散点
(ξ,ψ)在直角坐标系下的图像大致为:
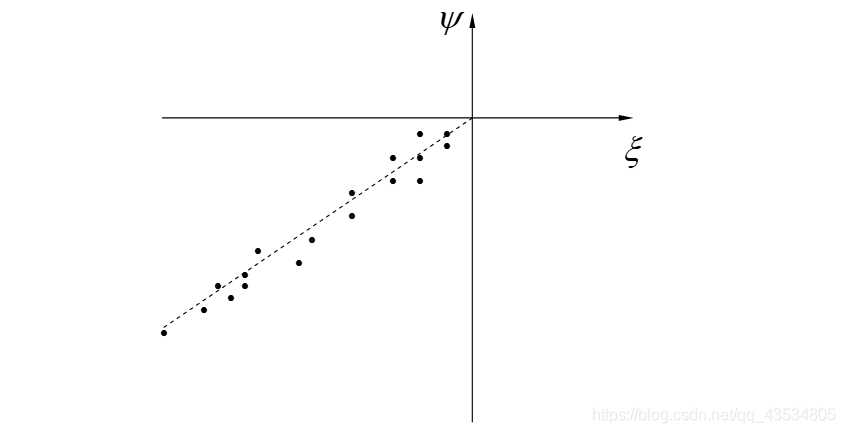
由图可知,大多数的点处在一条经过原点的直线附近,故
ξ和
ψ有如下关系:
ψ=γξ(0<γ<1) (3)
带入上式可得:
iQ(t)=iLγ(t)iK1−γ(t) (4)
记
a=Q(0)L−γ(0)K1−γ(0),则由(1)和(4)可知:
Q(t)=aLγ(t)K1−γ(t) (5)
式(5)就是经济学中著名的Douglas生产函数,它表明产量余劳动力、投资之间的关系,即:
QQ˙=γLL˙+(1−γ)KK˙ (6)
其中
Q˙、
L˙、
K˙表示Q、L、K关于t的导数。
这个函数表明,相对增长量,
QQ˙、
LL˙、
KK˙之间呈线性关系,当
γ→1时产量增长主要依靠劳动力增长,当
γ→0时产量增长主要依靠投资。亦称
γ为产量对劳动力的弹性系数
劳动生产率增长条件
定义劳动生产率
Z(t)=L(t)Q(t),则
ZZ˙=QQ˙−LL˙,将(6)代入
Z(t)可得:
ZZ˙=(1−γ)(KK˙−LL˙) (7)
由(7)可见,只要
KK˙>LL˙就能保证
ZZ˙>0,即劳动生产率的提高需要由投资的相对增长大于劳动力的相对增长为前提条件。
2.3存贮模型
原料、商品的存贮问题,存的太多,存贮费用过高;存的太少,无法及时满足需求。目的:制定最有存贮策略,即:多长时间顶一次货,每次顶多少货,才能使总费用最小。
模型一
模型假设
- 每次订货费用为
C1,每天每吨货物贮存费用为
C2(已知)
- 每天货物的需求量r吨为已知
- 订货周期为T天,每次订货Q吨,当贮存量降到0时订货立即到达。
模型建立
订货周期、订货量余每天的需求量存在关系:
Q=rT
订货以后贮存量
q(t)均匀地下降,即
q(t)=Q−rt,如下图:
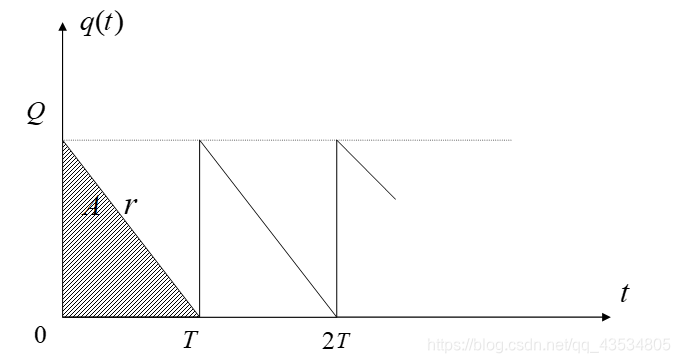
则一个订货周期的费用:
{订货费:C1,存贮费:∫0Tq(t)dt=21C2QT=21C2rT2
即:
C(T)=C1+21C2rT2
则一个订货周期每天的费用为:
C(T)=TC1+21C2rT
模型求解
令
dTdC=0,可求得:
T=RC22c1
进而:
Q=C22C1r
此模型称为经济订货批量公式,简称EOQ公式
模型二 允许缺货的存贮模型
模型假设
- 每次订货费用为
C1,每天每吨货物贮存费用
C2(已知)
- 每天的货物需求量r吨(已知)
- 订货周期为T天,订货量Q,允许缺货,每天每吨货物缺货费
C3(已知)
模型建立
缺货时的存储量q视为负值,则
q(t)的图像如下,货物在
t=T1时用完,于时
Q=rT1
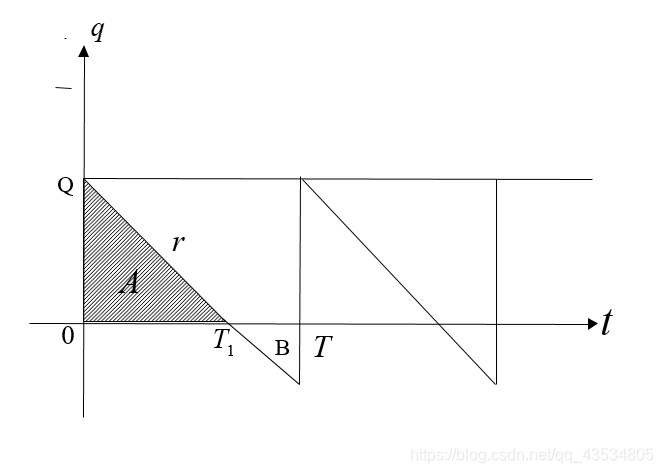
则一个订货周期内总费用为:
⎩⎪⎨⎪⎧订货费:C1,存贮费:∫0T1q(t)dt=21C2QT1=21C2rQ2,缺货费:∫T1T∣q(t)∣dt=2C3r(T−T1)2=2rC3(rT−Q)2
即:
C(T,Q)=C1+21C2Q2r1+2r1C3(rT−Q)2
则平均每天的费用为:
C(T,Q)=TC(T,Q)=TC1+2rTC2Q2+2rTC3(rT−Q)2
模型求解
{∂T∂C=0∂Q∂C=0
求出T、Q的最优解,分别记为
T′、Q′
T′=rC22C1C3C2+C3
,Q′=C22C1rC2+C3C3
分析
令
μ=C3C2+C3
,与模型一相比,有:
T′=μT,Q′=μQ
显然,T’ > T,Q’ < Q,即在允许缺货时应增大订货周期,减少订货批次;当缺货非
C3相对于存贮费
C2而言越大时,
μ越小,T’和Q’越接近T和Q。
2.4城市人口统计模型
模型一(估算城市现有人口)
城市人口密度常用
P(r)=r2+ab或者
P(r)=ae−br(a,b>0)来近似表示,其中r是距城中心的距离。则计算距离市中心C区域内的人口数N可以这样:从城市中心画一条射线,把这条线上从0到C之间n等分,每小区间长度为
Δr,每小区间确定一个圆环,第j个圆环面积为从城市中心为:
πrj2−πrj−12=πrj2−π(rj−Δr)2=2πrjΔr−π(Δr)2≈2πrjΔr
(Δr很小)
第j个圆环上的人口数近似为
P(rj)2πrjΔr,所以:
N≈∑j=1nP(rj)2πrjΔr
令
n→∞时,
N=∫0CP(r)2πrdr
模型二(预测城市未来人口)
P(t)表示t时刻的城市人口数量,人口变化手下面规则的影响:
- t时刻的净增长人口以每年r(t)的比率增加
- 在一段世界内,由于自然死亡和人口迁移,
T1时刻的人口数
P(T1)的一部分在
T2时刻仍然存在,用
h(T2−T1)P(T1)来表示,这里
0<h(T2−T1)<1,
T2−T1是这段时间的长度。
把(0,T]时间划分为n等分,每个小区间长度为
Δt。
假设初始时刻人口为P(0),到时刻T将只剩h(T)P(0)。当
Δt很小的时候,从
tj−1到
tj,净增长的人口比率近似为常数
r(tj)。这段时间净增的人口数近似为
r(tj)Δt,在
tj时刻的人口到T时刻只剩
h(T−tj)r(tj)Δt。所以在T时刻的总人口数近似为:
P(T)≈h(T)P(0)+∑j=1nh(T−tj)r(tj)Δt
令
n→∞,得:
P(T)=h(T)P(0)+∫0Th(T−t)r(t)dt
2.7古生物年代确定
主要思路:
C14的半衰期为5568年,根据
C14的蜕变减少量的变化来判断生物的死亡时间。
模型假设
- 地球周围大气的
C14可以认为不变,现代生物和古代生物体内的
C14蜕变速度一致。
- 由原子物理学,
C14的蜕变速度与该时刻的
C14含量成正比。
模型建立
记,
x(t)代表t时刻生物体内
C14的含量。由假设可知:
dtdx=−kx,k>0(1)
(1)的通解为
x(t)=Ce−kt,设生物死亡时间为
t0,代入可知,
C=x0,于时:
x(t)=x0e−kt(2)
记
C14的半衰期为T,则有:
x(T)=2x0(3)
将(3)代入(2)可得
k=Tln2,故可解得:
t=ln2Tlnx(t)x0(4)
由于
x0和x(t)难以测量,故使用另一种方法求t:
对(2)两边求导:
x′(t)=−x0ke−kt=−kx(t)
x′(0)=−kx(0)=−kx0
两式相除,可得:
x′(0)x′(t)=x(t)x0,代入(4)可得:
t=ln2Tlnx′(t)x′(0)
所以只需要测出标本
C14的平均蜕变速度(单位:次/分钟),即
x′(t),和现在的
C14的蜕变速度
x′(0),即可求出t。
2.8预测人口的增长
模型一:Malthhus指数增长模型
模型假设
1.某国/地区再t时刻的人口数x(t)为连续可微函数。
2.人口的增长率r是常数,即,单位时间人口的增长量与当时的人口成正比
模型建立
记
x0为初始时刻的人口,即
x(0)=x0
则从
t到
t+Δt内人口的增长量为:
x(t+Δt)−x(t)=rx(t)Δt
可导出下面的微分方程:
{dtdx=rxx(0)=x0
解得:
x(t)=x0ert,r>0
模型二:Logistic阻滞增长模型
模型假设
1.同模型一
2.当人口增加到一定数量后,增长率随着人口的继续增长而逐渐减少,且r(x)为x的线性函数
r(x)=r−sx,其中r为x=0时的增长率,成为固有增长率。
3.自然资源和环境条件所能容纳的最大人口数量为
xm,称作最大人口容量
模型建立
当
x=xm时,增长率为0,即
r(xm)=0,进而:
S=xmr,所以:
r(x)=r(1−xmx)
其中的
r,xm是根据人口统计数据确定的常数,
xm常由经验决定(模型缺点:
xm不易轻易地得到)。
模仿模型一可得:
{dtdx=r(1−xmx)xx(0)=x0
解得:
x(t)=1+(x0xm)e−rtxm
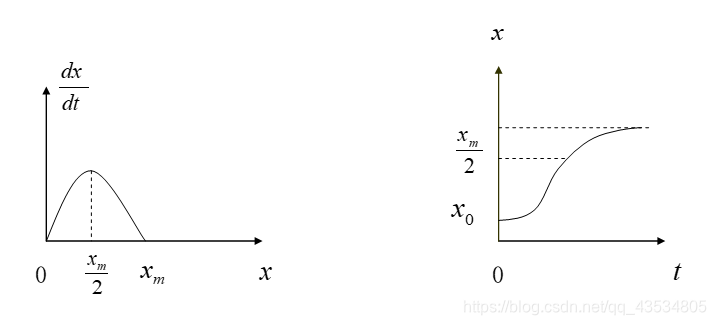
2.9药物在体内地分布与排除
模型背景
药物进入机体后,在随血液输送到各器官和组织的过程中,不断地被吸收、分布、代谢,最终排出体外。药物在血液中的浓度(
μg/mv)称血药浓度。血药浓度的大小直接影响到药物的疗效,浓度太低不能达到预期的治疗效果,浓度太高又可能导致中毒、副作用太强或造成浪费。
因此,研究药物在体内吸收、分布和排除的动态过程,对于新药研制时剂量的确定、给药方案设计等药理学和临床医学的发展具有重要的指导意义和实用价值。
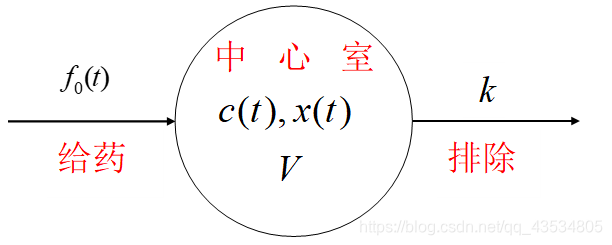
为了研究目的,将一个机体划分成若干个房室,每个房室是机体的一部分,比如中心室和周边室。在一个房室内药物呈均匀分布,而在不同的房室之间按一定规律进行转移。
模型假设
1.药物进入机体后,全部进入中心室(血液较丰富的心、肺、肾等器官和组织),中心室的容积在给药过程中保持不变;
2.药物从中心室排出体外,与排除的数量相比,药物的吸收可以忽略;
3.药物排除的速率与中心室的血药浓度成正比。
模型建立
f0(t):给药速度
c(t):中心室血药浓度
x(t):中心室药量
V:中心室容积
k:排除速率系数
求各种给药方式下血药浓度变化情况
上述变量有如下关系:
x˙=f0(t)−kx
即
x˙+kx=f0(x)
又
x(t)=Vc(t)
可得:
c˙(t)+kc(t)=Vf0(t)(1)
- 1.快速静脉注射(指数模型)
给药量为D,则初始条件
c(0)=VD,f0(t)=0
解得:
c(t)=VDe−kt(2)
- 2.恒速静脉注射
设持续时间为
τ,注射速率为
k0,则有:
当
(x≤t≤τ)时,
f0(t)=k0,初始条件为c(0)=0,
当
(t≥τ)时,
f0(t)=0,初始条件
c(τ)=Vkk0(1−e−kτ),所以(1)的解为:
c(t)={Vkk0(1−e−kt),0≤t≤τVkk0(1−e−kτ)e−k(t−τ),t≥τ(3)

- 3.口服或肌肉注射
在药物输入中心室之前先有一个将药物吸入血液的过程,可以看作有一个吸收室,药物由吸收室进入中心室,药物由吸收室进入中心室额转移速率系数记为
k1,给药量D,吸收室药量
x0(t)。则有:
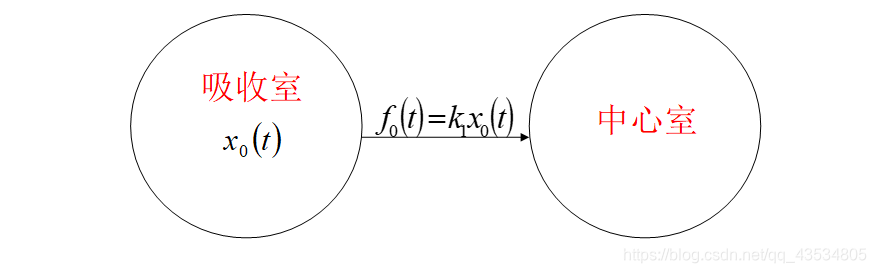
{x0˙=−k1x0x0(t)=D
上式可推出:
x0(t)=De−k1t
于时
f0(t)=k1De−k1t初始条件c(0)=0,(1)的解为:
c(t)=V(k1−k)k1D(e−kt−e−k1t),k1>k(4)
2.10导弹跟踪
背景
在发射导弹时刻(t=0),导弹位于坐标原点(0,0),飞机位于(a,b),飞机研平行于x轴的方向以常速
v0飞行。导弹在时刻t的位置为点(x,y),其速度为常值
v1,导弹在飞行过程中,按照制导系统时钟指向飞机。请确定导弹的飞行轨迹以及击中飞机所需的时间T。

模型建立与求解
首先建立导弹的运动方程。导弹飞行曲线在点M(x,y)处的切线方程为:
Y−y=dxdy(X−x)=dtdxdtdy(X−x)
其中(x,y)为切线上动点的坐标。由于点
A(xA,b)应位于切线上,且
xA=a+v0t,所以:
b−y=dtdxdtdy(a+v0t−x)
从而,导弹的飞行轨迹为:
{dtdx(b−y)=dtdy(a+v0−x)(1)(dtdx)2+(dtdy)2=v12(2)
由(1)可得:
dydx(b−y)=a+v0−x
两边对t求导,得:
d2yd2xdtdy(b−y)−dydxdtdy=v0−dtdx
即:
d2yd2xdtdy(b−y)=v0(3)
由(2)得:
(dtdy)2[1+(dtdydtdx)2]=v12
即:
dtdy=[1+(dydx)2]21v1
代入(3)可得导弹得运动方程:
d2yd2x(b−y)=λ[1+(dydx)2]21(4)
其中,
λ=v1v0,
又
x(0)=0,x(b)=a+v0T(在T时刻击中目标) (5)
接下来求(4)满足(5)的解:
设
p=dydx,则
dydp=dy2d2x,
(4)可化为:
dydp(b−y)=λ(1+p2)21(6)
ln[p+(1+p2)21]=−λln(b−y)+c1(7)
(6)的初始条件为
p(0)=ba,令
c1=ln(kbλ),则:
ln(p+1+p2
)=ln(b−y)−λ+ln(kbλ)=ln[(b−y)λkbλ]
p+1+p2
=(b−y)λkbλ
于时可以得到降阶方程:
dydx=21[(b−y)λkbλ−kbλ(b−y)λ]
其通解为:
x=21[(λ−1)(b−y)(λ−1)kbλ+(λ+1)kbλ(b−y)λ+1]+c(8)
根据初始条件x(0)=0,可得:
c=b[(1+k2)λ+k2−1]/2k(1−λ2)
所以导弹飞行轨迹方程为:
x=21[(λ−1)(b−y)(λ−1)kbλ+(λ+1)kbλ(b−y)λ+1]+b[(1+k2)λ+k2−1]/2k(1−λ2)
又由
x(b)=a+v0T得到导弹集中目标的时间为:
T=v0c−a=v1(1−λ2)a2+b2
−aλ(10)
2.11食饵-捕食者系统
一个包含两个群体的系统,其中一个群体紧密地依赖于另一个群体,成为食饵-捕食者系统。假设:x(t):t时刻食饵的数量;y(t):t时刻捕食者的数量。
如果各自独立生活,则:
{dtdx=λxdtdy=−μy(λ,μ>0)
如今两者生活在一起,则有:
{dtdx=(λ−αy)x(1)dtdy=−(μ−βx)y(2)(α,β>0)
上式称为Volterra-Lotka方程,初始条件为
x(0)=x0,y(0)=y0(1)/(2)可得:
dxdy=(λ−αy)x(βx−μ)y
可得通解:
−αy−βx+λlny+μlnx=lnc或
eαyyλeβxxμ=c
将初始条件代入,可得特解,是xoy面上的一条闭轨线
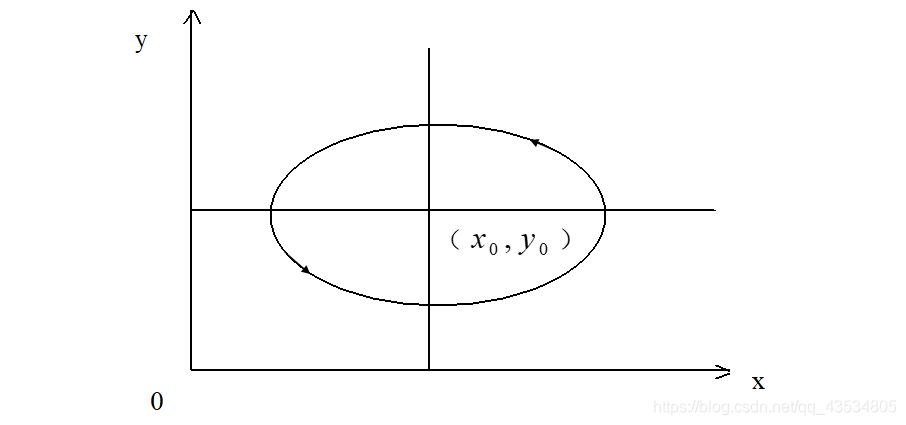
当食饵较多时,捕食者增多因而食饵必定减少,使得捕食者也随之减少,从而食饵又会增多。两者的数量如此起伏,周而复始,维持着生态平衡。
2.12传染病模型
背景
建立传染病模型的目的是描述传染过程、分析受感染人数的变化规律、预报高潮来到的时间。
为了简单起见,假设传播期间内所观察地区人数N不变,不计生死迁移,时间以天为单位。
模型一 SI模型
模型假设
- 1.人群分为健康者和病人,在t时刻这两类人所占比例分别为s(t),i(t),即s(t)+i(t)=1;
- 2.平均每个病人每天接触人数是常数
λ,即每个病人平均每天使得
λs(t)个健康者受感染变成病人,
λ称为日接触率。
模型建立
根据模型假设2,在T时刻,每个病人每天可以使得
λs(t)个健康者变成病人,病人人属为Ni(t),故每天新增
λNs(t)i(t)个患者,即:
Ndtdi=λNsi,假设t=0时患者比例
i0,可得模型:
{dtdi=λi(1−i)(1)i(0)=i0
式(1)的解为:
i(t)=1+(t01e−λt)1(2)
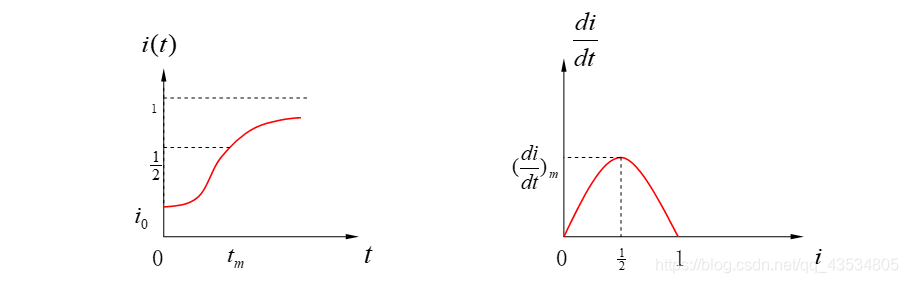
模型解释
- 1.当
i=21时,
dtdi达到最大值,此时
t=tm=λ−1ln(i01−1),也就是说,高潮到来时,
λ越大,则
tm越小。
- 2.当
t→∞时,
i→1此时所有的人都被感染,因为SI模型没有考虑治愈病人。
模型二 SIS模型
在SI模型的基础上引入治愈,对SI模型进行修正。
模型假设
- 1.同SI模型假设1
- 2.同SI模型假设2
- 3.病人每天被治愈的占病人总数的比例为
μ,称作日治愈率。
模型修正
SI模型可修正为,t时刻每天有
Niμ的病人转变为健康。
{dtdi=λi(1−i)−μi(3)i(0)=i0
(3)的解为:
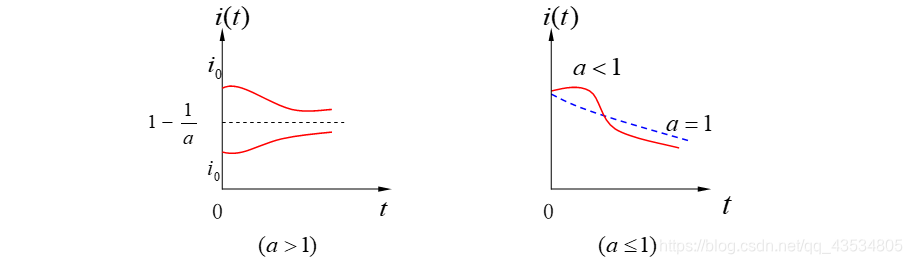
i(t)={[λ−μλ+(i01−λ−μλ)e−(λ−μ)t]−1,λ=μ(λt+i01)−1,λ=μ(4)
由(3)可以计算出使得
dtdi达到最大值的高潮时刻
tm(
dtdi的最大值
(dtdi)m在
i=2λλ−μ时达到)
记
a=μλ,可知:
i(∞)={1−a1,a>10,a≤1
SIR模型
模型假设
- 1.人群分为健康者、病人、移出者(病愈免疫者),三类人在t时刻在总人数N中占比例分别为s(t)、i(t)、r(t),即s(t)+i(t)+r(t)=1
- 2.病人日接触率为
λ,日治愈率为
μ,传染期间接触数
σ=μλ
模型建立
i(t)随t的变化规律同模型二,对于r(t):
Ndtdr=μNi,且dtds+dtdi+dtdr=0
于时可得模型:
⎩⎨⎧dtds=−λsidtdi=λsi−μi(5)s(0)=s0,i(0)=i0
从(5)中消去dt,结合
σ的实际意义,可得:
{dsdi=σs1−1(6)i∣s=s0=i0
(6)的解为:
i=(s0+i0)−s+σ1lns0s(7)
根据(5)(7)以及图像可分析s(t),i(t),r(t)的变化规律:
- 1.无论
s0,i0为多少,
i∞=0,即病人终将消失。
- 2.最终未被感染的健康者比例
s∞时方程
s0+i0−s∞+σ1lns0s∞=0(8)在
(0,σ1)内的单根。
- 3.若
s0>σ1,则当
s=σ1时,i(t)达到最大值
im=s0+i0−σ1(1+lnσs0),i(t)先增后减至0.
- 4.若
s0≤σ1,则
i(t)→0,s(t)→s∞。
模型解释
- 1.
σ1是一个阈值,当
s0>σ1时传染病会蔓延,
s0≤σ1时就不会蔓延
- 2.
σ=μλ表示
λ越小,
μ越大,
σ也越小,从而越有利。