Linear Algebra review - Inverse and transpose

摘要: 本文是吴恩达 (Andrew Ng)老师《机器学习》课程，第三章《线性代数回顾》中第19课时《逆和转置》的视频原文字幕。为本人在视频学习过程中记录下来并加以修正，使其更加简洁，方便阅读，以便日后查阅使用。现分享给大家。如有错误，欢迎大家批评指正，在此表示诚挚地感谢！同时希望对大家的学习能有所帮助。

In this video, I want to tell you about a couple of special matrix operations called the matrix inverse and the matrix transpose operation.

Inverse

Let's start by talking about matrix inverse, and as usual we'll start by thinking about how it relates to real numbers. In the last video, I sai that the number $1$ plays the role of the identity in the space of real numbers because $1$ times anything is equal to itself. It turns out that real numbers have this property that each number has an inverse. For example, given the number three, there exists some number, which happens to be three inverse. That number times three gives you back the identity element $1$ . And three inverse of course this is just one third. Now it turns out that in space of real numbers, not everything has an inverse. For example, the number zero does not have an inverse. In the next of this section, we'll try to compute the inverse of matrix.

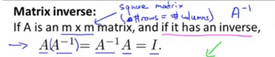
If A is an $m\times m$ matrix, and if it has an inverse, then the inverse is going to be written $A^{-1}$ . And $AA^{-1}=A^{-1}A=I$ , is going to give us back the identity matrix. Only matrices that are $m\times m$ for some value of $m$ have an inverse. So, a matrix is $m\times m$ , this is also called a square matrix. And it turns out only square matrices have inverses. So $A$ is a square matrix, so is $m\times m$ , and if it's inverse, then it satisfies this equation over here.

Let's take a look at a concrete example. Let's say I have a matrix $\begin{bmatrix} 3 & 4\\ 2 & 16 \end{bmatrix}$ . So this is a $2\times 2$ square matrix, and so this matrix could have an inverse. It turns out that, I happen to know the inverse of this matrix is $\begin{bmatrix} 0.4 & -0.1\\ -0.05 & 0.075 \end{bmatrix}$ . If I multiply them together, it turns out what I get is the $2\times 2$ identity matrix.

>> A = [3 4; 2 16]

A =

3 4
2 16

>> pinv(A)
ans =

0.400000 -0.100000
-0.050000 0.075000

>> inverseOfA = pinv(A)
inverseOfA =

0.400000 -0.100000
-0.050000 0.075000

# Note that those numbers off the diagonals are actually 0

>> A * inverseOfA
ans =

1.0000e+00 5.5511e-17
-2.2204e-16 1.0000e+00

>>

>> inverseOfA * A
ans =

1.00000 -0.00000
0.00000 1.00000

So how did I find this inverse? It turns out there is very good numerical software for taking a matrix and computing its inverse. Let me show you an example how I actually computed this inverse. And what I did was I used software called Octave. Let me quickly show you an example. Set my matrix $A$ to be equal to that matrix on the left ( $\begin{bmatrix} 3 & 4\\ 2 & 16 \end{bmatrix}$ ). And the software let me compute the $A^{-1}$ very easily.

In my definition of what the inverse of a matrix is, I had this caveat right?

Firstly it always must be a square matrix.
It turns out that if $A$ is say the matrix of all zeros, then this matrix $A$ also does not have an inverse, because there's no $A^{-1}$ matrix, that this matrix times some other matrix will give you an identity matrix.

And there are a few other matrices with properties similar to this, that also don't have an inverse. But it turns out that I don't want to go too deeply into what it means for a matrix have an inverse. But it turns out that for our machine learning application, this shouldn't be an issue. Or more precisely, for the learning algorithms, where this may be an issue, namely whether or not an inverse matrix appears. I will tell when we get to those learning algorithms, just what it means for an algorithm to have or not have an inverse, and how to fix it in case of end up working with matrices that don't have inverses. But the intuition if you want is that you can think of matrices that don't have an inverse that is somehow too close to zero in some sense.

So just to wrap up the terminology, matrix that don't have an inverse sometimes is called a singular matrix(奇异矩阵), or degenerate matrix(退化矩阵), So this matrix over here ( $\begin{bmatrix} 0 & 0\\ 0 & 0 \end{bmatrix}$ ) is an example of a matrix that is singular, or a matrix that is degenerate.

Transpose

Finally, the last special matrix operation is the matrix transpose. Suppose I have matrix $A$ . If I compute the transpose of $A$ , that's what I get on the right. This is a transpose, which is written $A^{T}$ . And the way you compute the transpose of matrix is as follows. To get a transpose, I wanna first take the first row of $A$ , $\begin{bmatrix} 1 & 2 & 0 \end{bmatrix}$ . That becomes the first column of this transpose. And then I'm going to take the second row of $A$ , $\begin{bmatrix} 3 & 5 & 9 \end{bmatrix}$ , and that becomes the second column of the matrix $A^{T}$ . Another way of thinking about how to compute transposes is as if you're taking this sort of $45$ degree axis, you're mirroring or you're flipping the matrix along that $45$ degree axis.

So here's the more formal definition of a matrix transpose. Let's say $A$ is a $m\times n$ matrix, and let's set $B= A^{T}$ , and we say $B$ equals $A^{T}$ like so. Then $B$ is going to be a $n\times m$ matrix, with the dimensions reversed. And moreover, $B_{ij}=A_{ji}$ .

For example, $B_{12}=A_{21}$ , which is equal to $3$ .

<end>

王彩旗

发布了41 篇原创文章 · 获赞 12 · 访问量 1306

私信关注