本人CSDN博客专栏:https://blog.csdn.net/yty_7
Github地址:https://github.com/yot777/
散点图的直观解决思路:更近
回到上一节:杨桃的Python机器学习5,我们最终得到了如下的散点图:

蓝色的点(标签为1)似乎都集中在图的左下部分,橙色的点(标签为0)似乎都集中在图的右上部分。
我们在散点图上再增加两个点A和B,想想他们的标签应该分别是什么?

同学们也许大概已经猜出来答案了:
点A和蓝色的点更近,应当是标签1
点B和橙色的点更近,应当是标签0
现在这个“更近”只是直观上的感觉,有没有更科学的计算呢?当然有!这就是欧式距离公式。
一维的距离度量
我们先以一维直线举例,如图:

如图所示,一维直线上有A和B两个点,A点在0的位置,B在5的位置。A点和B点的距离是:|AB|=|5-0|=5
现在增加一个C点在2的位置,请问C点离哪个点更近?
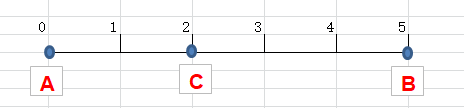
答案是显而易见的,计算两点之间的距离就能知道结果。
C点到A点的距离是:|CA|=|2-0|=|2|=2
C点到B点的距离是:|CB|=|2-5|=|-3|=3 (绝对值)
|CA| < |CB|,因此C点离A点更近。
一般的,两个点 在一维长度的距离公式就是
二维的距离度量
现在我们把问题稍微复杂一点,从一维直线拓展到二维平面,如图:

A点的位置坐标是(0, 0),B点的位置坐标是(3, 4),现在求AB之间的距离(即红线长度)是多少?
可能有同学一下子就看出来了:这不就是勾股定理嘛?勾三股四弦五!完全正确!具体计算如下:
也就是说,二维平面上两点的距离公式是:横坐标之差的平方,加上纵坐标之差的平方,再开根号即可。
现在,我们在上图增加一个C点,位置坐标是(5, 2),再分别求C点到A点和B点的距离(即蓝线和橙线长度):

将A点、B点、C点的坐标分别代入二维平面上两点的距离公式,即得:
|CB| < |CA|,因此C点离B点更近。
三维的距离度量
直接上公式吧,有兴趣的同学可以自己画图推导:
需要注意的是,三维距离公式只是在二维距离公式的基础上,增加了一个竖直方向的维度z
每个维度之间的距离仍然是计算差的平方,然后把所有维度的差的平方求和,最后开平方根。
千万不要以为三维就是开立方根啊!
n维的距离度量:欧式距离公式
当维度超过三维的时候,就很难用直观画图的形式展现出距离了。怎么计算呢?
第一步,我们需要把一维二维三维中点的坐标抽象成向量的表达形式,即
,
再次强调,向量用小写字母表示,矩阵用大写字母表示!
在之前一维举例中,,
,
在之前二维举例中,,
,
在三维中
推广到n维,距离公式是:
这就是欧式距离公式。
再回到本节最初的分类问题:

我们可以用欧式距离公式得到点A到散点图中每一个点的距离。
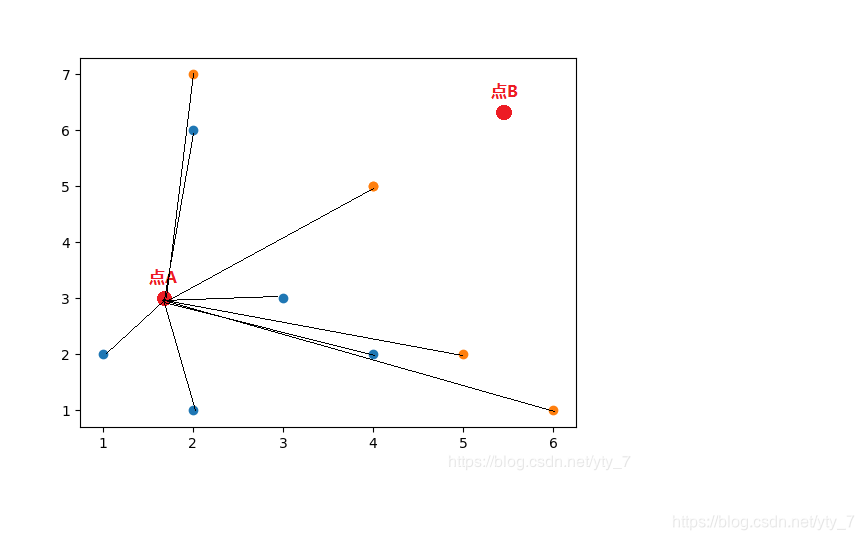
得到距离之后呢?请看下一节的讲解。
总结
散点图的直观解决思路:找距离更近的点。
欧式距离公式:
一维情况下:
二维情况下:
三维情况下:
本人CSDN博客专栏:https://blog.csdn.net/yty_7
Github地址:https://github.com/yot777/
如果您觉得本篇本章对您有所帮助,欢迎关注、评论、点赞!Github欢迎您的Follow、Star!
