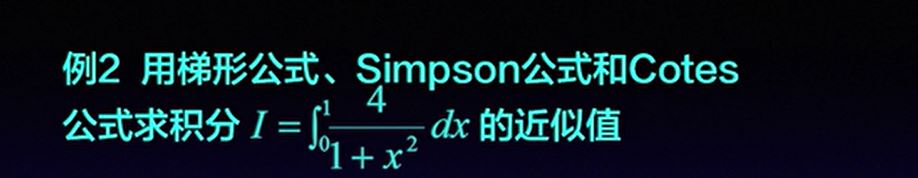HFUT.计算方法(一) - Chp6 数值积分(二)
目录
chp6.4 Newton-Cotes求积公式
Simpson公式
\[\int_{a}^{b} f(x) d x \approx \frac{b-a}{6}\left[f(a)+4 f\left(\frac{a+b}{2}\right)+f(b)\right]=S \tag{1} \]
Simpson公式或抛物线公式,记为\(S\).
容易证明Simpson公式对不高于三次的多项式精确成立,即
\[\int_{a}^{b} p_{3}(x) d x=\frac{b-a}{6}\left[p_{3}(a)+4 p_{3}\left(\frac{a+b}{2}\right)+p_{3}(b)\right] \tag{2} \]
-
求积误差:
构造三次多项式,使满足:
\[H_3(b) = f(b), H_{3}(b)=f(b), H_{3}\left(\frac{a+b}{2}\right)=f\left(\frac{a+b}{2}\right), H_{3}^{\prime}\left(\frac{a+b}{2}\right)=f^{\prime}\left(\frac{a+b}{2}\right) \]
\[f(x)-H_{3}(x)=\frac{f^{(4)}\left(\xi_{x}\right)}{4 !}(x-a)\left(x-\frac{a+b}{2}\right)^{2}(x-b), \quad \xi_{x} \in(a, b) \tag{3} \]
有:
$$\begin{aligned}
R[f] &=\int_{a}^{b} f(x) d x-\frac{b-a}{6}\left[f(a)+4 f\left(\frac{a+b}{2}\right)+f(b)\right] \
&=\int_{a}^{b} f(x) d x-\frac{b-a}{6}\left[H_{3}(a)+4 H_{3}\left(\frac{a+b}{2}\right)+H_{3}(b)\right] \
&=\int_{a}^{b} f(x) d x-\int_{a}^{b} H_{3}(x) d x \
&=\frac{1}{4 !} \int_{a}^{b} f{(4)}\left(\xi_{x}\right)(x-a)\left(x-\frac{a+b}{2}\right){2}(x-b) d x \
&=\frac{f^{(4)}(\eta)}{4 !} \int_{a}{b}(x-a)\left(x-\frac{a+b}{2}\right){2}(x-b) d x \
&=-\frac{(b-a)^{5}}{2880} f^{(4)}(\eta), \quad \eta \in(a, b)
\end{aligned}$$
Newton-Cotes公式
-
Newton-Cotes公式的截断误差
\[R[f]=\left\{\begin{array}{l} \frac{f^{(n+1)}(\eta)}{(n+1) !} \int_{a}^{b} \omega_{n+1}(x) d x \quad(n为奇数) \\\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \eta\in(a, b)\\\frac{f^{(n+2)}(\eta)}{(n+2) !} \int_{a}^{b} x \omega_{n+1}(x) d x \quad(n为偶数) \end{array}\right.\] -
代数精度
- n+1个节点的插值型求积公式至少具有n次代数精度
- n是偶数时 Newton-Cotes公式具有n+1次代数精度。
例题
- 例题1

- 例题2
解答
- 例题1解答

- 例题2解答