【机器学习】隐马尔可夫模型（上）——定义及相关概率计算

前言：隐马尔可夫模型（Hidden Markov Model, HMM）是可用于标注问题（即输入输出都是离散序列的监督学习问题）的统计学模型，描述由隐藏的马尔可夫链随机生成观测序列的过程，属于生成模型。本文首先介绍马尔可夫过程和隐马尔可夫模型的基本概念，然后分别叙述和实现隐马尔可夫模型的概率计算算法、学习算法以及预测算法。

一、马尔可夫过程
马尔可夫过程 (Markov Process)，因俄罗斯数学家安德烈 · 马尔可夫而得名，代表数学中具有马尔可夫性质的离散随机过程。该过程中，每个状态的转移只依赖于之前的 n 个状态，这个过程被称为1个 n 阶的模型，其中 n 是影响转移状态的数目。我们称该过程具有马尔可夫性或无后效性。通俗的说，在已经知道过程“现在”的条件下，其“将来”不依赖于“过去”。最简单的马尔科夫过程就是一阶过程，每一个状态的转移只依赖于其之前的那一个状态。注意这和确定性系统不一样，因为这种转移是有概率的，而不是确定性的。时间和状态都是离散的马尔可夫过程就称为马尔可夫链，记为$\{X_n=X(n), n=0,1,2,\cdots\}$，它可以看作时间集$T_1=\{0,1,2,\cdots\}$上对离散状态的马氏过程相继观察的结果。这些变量的取值范围，即它们所有可能取值的集合，被称为“状态空间”，记为$I=\{a_1, a_2, \cdots\}$。马尔可夫性通常可用条件分布律来表示：

$$P(X_{m+n}=a_j|X_{t_1}=a_{i_1}, X_{t_2}=a_{i_2},\cdots,X_m=a_i)=P(X_{m+n}=a_j|X_m=a_i)$$
这个条件概率称为马氏链在时刻 $m$处于状态 $a_i$条件下，在时刻 $m+n$转移到状态 $a_j$的 状态转移概率。通常情况下我们研究的是 $n=1$即单步转移的情况。一般来说，一个含有 $N$的状态的一阶过程有 $N^2$种状态转移。所有概率可以用一个 状态转移概率矩阵表示：
$$\begin{bmatrix} p_{11} & p_{12} & \cdots p_{1j}\cdots \\ p_{21} & p_{22} & \cdots p_{2j}\cdots \\ \vdots & \vdots & \vdots \\ p_{i1} & p_{i2} & \cdots p_{ij}\cdots \\ \vdots & \vdots & \vdots \\ \end{bmatrix}$$
该矩阵有约束条件： $p_{ij}\ge0$, $\sum_{j=1}^N p_{ij} = 1$, 即每一行元之和等于1.
然而，当马尔科夫过程不够强大的时候，我们又该怎么办呢？在某些情况下，马尔科夫过程不足以描述我们希望发现的模式。
例如，一个隐居的人可能不能直观的观察到天气的情况，但是民间传说告诉我们海藻的状态在某种概率上是和天气的情况相关的。在这种情况下我们有两个状态集合，一个可以观察到的状态集合（海藻的状态）和一个隐藏的状态（天气状况）。我们希望能找到一个算法可以根据海藻的状况和马尔科夫假设来预测天气的状况。
一个更现实的例子是语音识别，我们听到的声音是声带、喉咙和一起其他的发音器官共同作用的结果。这些因素相互作用，共同决定了每一个单词的声音，而一个语音识别系统检测的声音（可以观察的状态）是人体内部各种物理变化（隐藏的状态、引申一个人真正想表达的意思）产生的。
某些语音识别设备把内部的发音机制作为一个隐藏的状态序列，把最后的声音看成是一个和隐藏的状态序列十分相似的可以观察到的状态的序列。在这两个例子中，一个非常重要的地方是隐藏状态的数目和可以观察到的状态的数目可能是不一样的。在一个有3种状态的天气系统（sunny、cloudy、rainy）中，也许可以观察到4种潮湿程度的海藻（dry、dryish、damp、soggy）。在语音识别中，一个简单的发言也许只需要80个语素来描述，但是一个内部的发音机制可以产生不到80或者超过80种不同的声音。
在上面的这些情况下， 可以观察到的状态序列和隐藏的状态序列是概率相关的。于是我们可以将这种类型的过程建模为有一个 隐藏的马尔科夫过程和一个与这个隐藏马尔科夫过程概率相关的并且可以观察到的状态集合。这就是本文重点介绍的 隐马尔可夫模型。

二、隐马尔可夫模型的定义
隐马尔可夫模型 (Hidden Markov Model) 是一种统计模型，用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数，然后利用这些参数来作进一步的分析。下图是一个三个状态的隐马尔可夫模型状态转移图，其中x 表示隐含状态，y 表示可观察的输出，a 表示状态转换概率，b 表示输出概率：

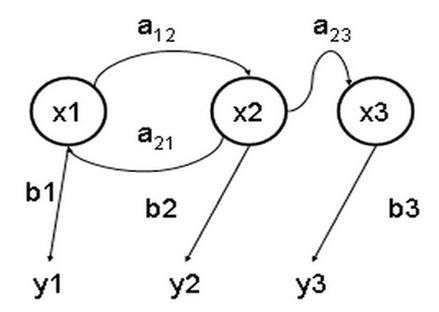
HMM的完整定义如下：
设$Q$是所有可能的状态的集合，$V$所有可能的观测结果的集合。

$$Q=\{q_1, q_2, \cdots , q_N\}, V=\{v_1, v_2, \cdots , v_N\}$$
其中N是可能的状态数，M是可能的观测数。
设 $I$是长度为 $T$的状态序列， $O$是对应的观测序列.
$$I=(i_1, i_2, \cdots , i_T), O=(o_1, o_2, \cdots , o_T)$$
$A$是状态转移矩阵： $A=[a_{ij}]_{N\times N}$
其中， $$a_{ij}=P(i_{t+1}=q_j|i_t=q_i), i=1,2,\cdots,N; j=1,2,\cdots,N$$
是在时刻 $t$处于状态 $q_i$的条件下在时刻 $t+1$转移到状态 $q_j$的概率。
B是观测概率矩阵： $$B=[b_j(k)]_{N\times M}$$
其中， $$b_j(k)=P(o_t=v_k|i_t=q_j), k=1,2,\cdots,M; j=1,2,\cdots ,N$$
是在时刻 $t$处于状态 $q_j$的条件下生成观测 $v_k$的概率。
$\pi$是初始状态概率向量： $\pi=(\pi_i)$
其中， $$\pi_i=P(i_1=q_i), i=1,2,\cdots,N$$
是时刻 $t=1$处于状态 $q_i$的概率。
隐马尔可夫模型由初始状态概率向量 $\pi$、状态转移概率矩阵 $A$和观测概率矩阵 $B$决定。 $\pi$和 $A$决定状态序列， $B$决定观测序列。因此，隐马尔可夫模型 $\lambda$可以用三元符号表示，即 $$\lambda=(A, B, \pi)$$
从定义知，HMM作了两个基本假设：
(1)齐次马尔可夫性假设，即假设隐藏的马尔可夫链在任意时刻 $t$的状态只依赖于其前一时刻的状态，与其他时刻的状态及观测无关，也与时刻 $t$无关。 $$P(i_t|i_{t-1}, o_{t-1}, \cdots, i_1, o_1)=P(i_t|i_{t-1}), t=1,2,\cdots,T$$
(2)观测独立性假设，即假设任意时刻的观测只依赖于该时刻的马尔可夫链的状态，与其他观测及状态无关。 $$P(o_t|i_T,o_T,i_{T-1},o_{T-1},\cdots,i_{t+1},o_{t+1},i_t,o_{t-1},\cdots,i_1,o_1)=P(o_t|i_t)$$
三、隐马尔可夫模型的3个基本问题
(1)概率计算问题。给定模型 $\lambda=(A,B,\pi)$和观测序列 $O=(o_1,o_2,\cdots,o_T)$，计算在模型 $\lambda$下观测序列 $O$出现的概率 $P(O|\lambda)$。
(2)学习问题。已知观测序列 $O=(o_1,o_2,\cdots,o_T)$，估计模型 $\lambda=(A,B,\pi)$的参数，使得在该模型下观测序列概率 $P(O|\lambda)$最大，即用极大似然估计的方法估计参数。
(3)预测问题，也称为解码(decoding)问题。已知模型 $\lambda=(A,B,\pi)$和观测序列 $O=(o_1,o_2,\cdots,o_T)$，求对给定观测序列条件概率 $P(I|O)$最大的状态序列 $I=(i_1,i_2,\cdots,i_T)$。即给定观测序列，求最有可能的对应状态序列。

四、概率计算算法
1.直接计算法
直接按照定义得到的计算公式是

$$P(O|\lambda)=\sum_{i_1,i_2,\cdots,i_T}\pi_{i_1}b_{i_1}(o_1)a_{i_1i_2}(o_2)\cdots a_{i_{T-1}i_T}b_{i_T}(o_T)$$
但是利用这条公式计算量非常大，概念上可行，实际上不可取。
2.前向算法
前向概率：给定隐马尔可夫模型 $\lambda$，定义到时刻 $t$部分观测序列为 $o_1,o_2,\cdots,o_t$且状态为 $q_i$的概率为前向概率，记作 $$\alpha_t(i)=P(o_1,o_2,\cdots,o_t,i_t=q_i|\lambda)$$
算法：
输入：HMM的参数 $\lambda$，观测序列 $O$；
输出：观测序列概率 $P(O|\lambda)$.
(1)初值 $$\alpha_1(t)=\pi_ib_i(o_1), i=1,2,\cdots,N$$
(2)递推：对 $t=1,2,\cdots,T-1$， $$\alpha_{t+1}(i)=\left[\sum_{j=1}^N\alpha_t(j)a_{ji}\right]b_i(o_{t+1}), i=1,2,\cdots,N$$
(3)终止 $$P(O|\lambda)=\sum_{i=1}^N\alpha_T(i)$$
相关证明可查阅相关论文。下面给出代码实现。
我们考虑盒子和球模型：总共有三个盒子，box1, box2, box3。每个盒子里面装着一定数量的红白两色小球。从这3个盒子中随机抽出一个，并从这个盒子随机抽出一个球，记录颜色后放回。如此进行下去便得到一个球的颜色的观测序列，例如 $O=\{red, write, red\}$。在这个过程中，观察者只能观测到球的颜色序列，观测不到球是从哪个盒子取出来的。这样就形成了一个简单隐马尔可夫模型。

class HMM:
    def __init__(self, pi, A, B):
        self.pi = pi
        self.A = A
        self.B = B
        self.M = B.shape[1]
        self.N = A.shape[0]

def forward(hmm, obs):
    T = len(obs)    # 观察序列长度
    N = hmm.N       # 隐藏层状态数
    alpha = matrix(zeros((N,T)))    # 前向概率
    alpha[:,0] = multiply(hmm.pi[:], hmm.B[:,observation.index(obs[0])])    # 初值 
    for t in range(1,T):    # 递推
            for n in range(0,N):
                alpha[n,t] = sum(alpha[:,t-1].T * hmm.A[:,n]) * hmm.B[n,observation.index(obs[t])]
    prob = sum(alpha[:,T-1])    # 计算观察序列概率
    return prob, alpha

测试代码如下：

if __name__ == "__main__":
    # 状态转移概率矩阵
    A = matrix([[0.5,0.2,0.3],
                [0.3,0.5,0.2],
                [0.2,0.3,0.5]])
    # 观测概率矩阵
    B = matrix([[0.5,0.5],
                [0.4,0.6],
                [0.7,0.3]])
    pi = matrix([0.2,0.4,0.4]).T
    hmm = HMM(pi, A, B)
    observation = ['red','write']# 所有可能的观测集合
    observed = ['red','write','red']# 观测序列
    prob, alpha = forward(hmm, observed)
    print('The forword probability is: \n', alpha)
    print('The probability of this observed sequence is %f' % prob)

计算结果为：

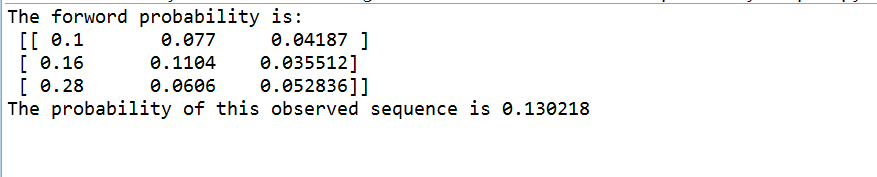
计算结果和手算结果一致。

3.后向算法
后向概率：给定隐马尔可夫模型$\lambda$，定义到时刻$t$状态为$q_i$的条件下，从$t+1$到$T$的部分观测序列为$o_{t+1},o_{t+2},\cdots,o_T$的概率后向概率，记作

$$\beta_t(i)=P(o_{t+1},o_{t+2},\cdots,o_T|i_t=q_i, \lambda)$$
算法：
输入：HMM的参数 $\lambda$，观测序列 $O$；
输出：观测序列概率 $P(O|\lambda)$.
(1) $$\beta_T(i)=1, i=1,2,\cdots,N$$
(2)对 $t=T-1,T-2,\cdots,1$
$$\beta_t(i)=\sum_{j=1}^Na_{ij}b_j(o_{t+1})\beta_{t+1}(j), i=1,2,\cdots,N$$
(3) $$P(O|\lambda)=\sum_{i=1}^N\pi_ib_i(o_1)\beta_1(i)$$

代码实现如下：

def backward(hmm, obs):
    T = len(obs)    # 观察序列长度
    N = hmm.N       # 隐藏层状态数
    beta = matrix(zeros((N,T)))    # 后向概率
    beta[:,T-1] = 1
    for t in reversed(range(0,T-1)):
        for n in range(0,N):
            beta[n,t] = sum(multiply(multiply(hmm.A[n,:].T, hmm.B[:,observation.index(obs[t+1])]), beta[:,t+1]))
    prob = sum(multiply(multiply(hmm.pi, hmm.B[:,observation.index(obs[0])]), beta[:,0]))
    return prob, beta

同样的测试输入

    prob2, beta = backward(hmm, observed)
    print('The backward probability is: \n', beta)
    print('The probability of this observed sequence is %f' % prob2)

测试结果为：

关于学习算法和预测算法，将在下一篇博文讲述。To be continue……