LCA算法之倍增
这里写一篇关于LCA算法倍增的博客。
倍增是LCA暴力之后的优化~
所以应该比较简单。但是我理解来理解去,理解了一下午??你敢信??
LCA(Least Common Ancestors)最近公共祖先
什么是最近公共祖先??
就是深度最大的公共祖先
例如下面一棵树
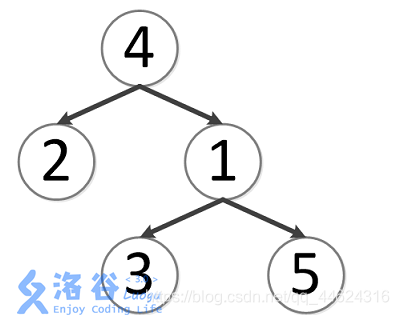
结点3和结点5的最近公共祖先是1;
结点2和结点3的最近公共祖先是4;
结点1和结点4的最近公共祖先是4;
上面说了嘛。倍增是暴力的优化。所以我们先看看暴力的思路:
倍增是利用二进制的一些特性=-=可以通过数据之间的关系来快速进行运算。(我们知道任何数都可以化成2进制的式子)
我们首先要把各个结点的深度求出来。
比如我们要去求3和2的LCA。
我们求得dep[结点3] = 2;
dep[结点2] = 1;
我们首先要把这两个结点放在同一层。(也就是深度一样才可以)
深度一样后我们再把两只结点一起跳
跳到结点相同即可,但是这样一个一个的处理会不会太麻烦了呢?
有什么优化的地方吗?
有的~
就是我们跳的时候优化。跳2的倍数。
fa[i][j]表示结点i跳2^j次方后的位置,也就是说2 ^ j次方代的祖先
预处理出往上走2^j次方的主线。
显然当j = 0的时候,i走到的是i的父结点
举个例子:
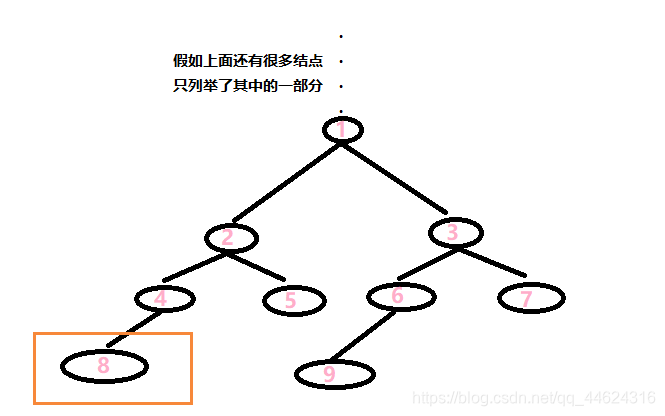
假如我们从第八个结点开始往上。
当j = 0的时候,显然我们往上走了一格。到达了8的父亲结点(同时也是祖先结点)4
当j = 1的时候,2^j = 2,我们向上走了两格。到达祖先结点2的位置
考虑:当走了2^j格的时候我们能否从前面的路径找到应该去的位置(而不是一层一层的跳)
数学:2^j = 2 ^ (j - 1) * 2 = 2 ^ (j - 1) + 2 ^ (j - 1);
所以递推式出来了:
fa[i][j] = fa[ fa[i][j - 1] ][j - 1];
这个式子什么意思?
是说我们先跳到2^( j - 1)次方的祖先的位置。然后从当前位置开始,再次跳到这个位置的2 ^ (j - 1)次方的祖先的位置。
这样我们就可以从前开始处理出来的路线求解未知的路线。(达到优化)
此时预处理完毕。
当我们求解的两个结点的深度不一样的时候。我们需要把深度较大的结点往上移。使得与深度较小的结点平齐。
举个例子:
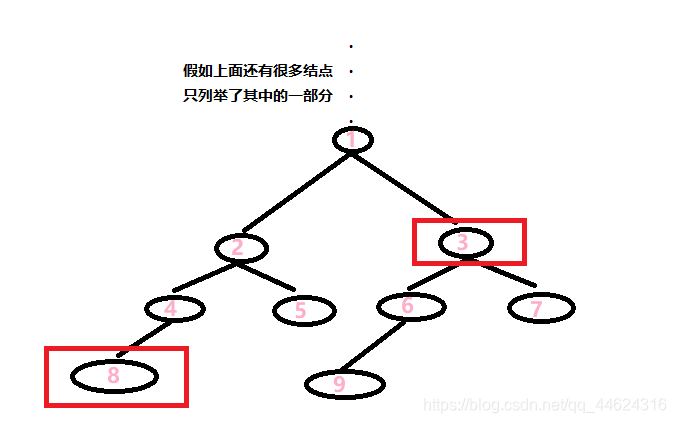
当前结点8和结点3的深度不一致。
我们需要把结点8向上移动。移动到与结点3相同深度的地方(此时这里假设结点3的深度为1,结点8的深度为3)
考虑:8的二进制表示:1000
8 = 2 ^ 3;
我们跳2^3次方,不行。深度比结点3的小了。
跳2^2次方,不行。还是跳多了。
跳2^1次方,跳两步。可以。到达结点2.与结点3平齐。
这个地方的处理是从大到小的处理的。(指数从大到小,上面式子观察)
或者这样说:5 = 2^2 + 2 ^ 0;(指数从大到小)
如果从小到达呢?(可能会发生“悔棋”现象。5 != 2 ^ 0 + 2 ^ 1 + 2 ^ 2;
所以这里需要从大往小处理。
两个结点的高度在同一层了,现在需要一起往上跳。
这个地方我们只能从小往大处理。
因为两个结点的公共祖先可能不止一个。
如果从大往小处理的话可能直接跳过了最近的公共祖先。跑到其他的公共祖先上去了(不是最近)
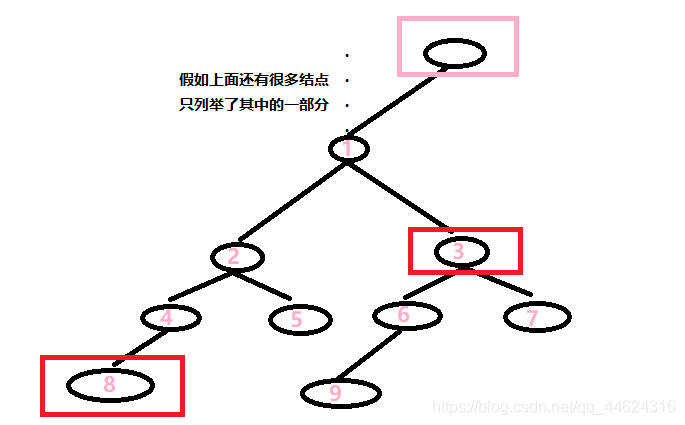
比如上面过程把结点8处理到了结点2,然后从结点2和结点3的位置往上跳。如果从大的开始处理,我们可能直接跳到粉色框框的祖先上去了。而错过了最近公共祖先结点1的位置。(得到错误答案)
所以一起跳的时候是从小的指数开始。
我们每次跳如果他们的父亲结点不相等。我们就继续更新往上跳。如果父亲结点相等了,我们就不跳了,返回任意一个结点的父亲结点即可(反正父亲一样~)
这就是倍增的基本思路了~
代码中特判了一下(有可能要求的某一个结点就是LCA,所以当处理到高度相同的时候两个结点相等,就可以直接返回了)
这里参考的洛谷P3379LCA模板题给的模板代码:

代码部分有一个预处理的lg[]数组。
意思是:当前深度最多可以跳的2的(lg[i] - 1)次方步数(这里的最多是一次性跳的最大步数)
lg[] = {0, 1, 2, 2, 3, 3, 3, 3, 4…};
比如深度为1的时候lg[1] = 1;最多可以跳2^(1 - 1) = 1步
(树的高度到20层就不得了了,也可以直接循环写出来判断。但lg[]这样写节约时间)
代码使用邻接表存储的:洛谷这里卡vector,所以用邻接表。还卡cin。用scanf();
这都是走出来的心酸路啊。。
to指的是下一个结点。
next指的是与当前结点有路线相邻的结点。
add()函数:
head[]记录:下标记录的是结点的编号,里面的值记录的是结点编号所对应的是哪一个edge[i];
由于输入部分结点可能不止输入1次。那么edge[]对应的也发生改变。需要更新head[];
同时用next把这些结点联系起来。(next存储的是edge[i],也就是head[]的内容)
如果当前结点为叶子。那么next就为0;(dfs处理当前深度就处理完了)
模板代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
struct node
{
int to;
int next;
}edge[N << 1];
int head[N];
int n, m, s;
int cnt;
int lg[N];
int dep[N];
int fa[N][25];
void add(int x, int y)
{
edge[++cnt].to = y;
edge[cnt].next = head[x];
head[x] = cnt;
}
void dfs(int now, int fath)
{
fa[now][0] = fath;
dep[now] = dep[fath] + 1;
for (int i = 1; i <= lg[dep[now]]; i++)
{
fa[now][i] = fa[fa[now][i - 1]][i - 1];
}
for (int i = head[now]; i; i = edge[i].next)
{
if (edge[i].to != fath)
{
dfs(edge[i].to, now);
}
}
}
int LCA(int x, int y)
{
if (dep[x] < dep[y])
{
swap(x, y);
}
while (dep[x] > dep[y])
{
x = fa[x][lg[dep[x] - dep[y]] - 1];
}
if (x == y)
{
return x;
}
for (int k = lg[dep[x]] - 1; k >= 0; k--)
{
if (fa[x][k] != fa[y][k])
{
x = fa[x][k];
y = fa[y][k];
}
}
return fa[x][0];
}
int main()
{
scanf ("%d%d%d", &n, &m, &s);
for (int i = 1; i < n; i++)
{
int u1, u2;
scanf ("%d%d", &u1, &u2);
add(u1, u2);
add(u2, u1);
}
for (int i = 1; i <= n; i++)
{
lg[i] = lg[i - 1] + (1 << lg[i - 1] == i);
}
dfs(s, 0);
for (int i = 1; i <= m; i++)
{
int x, y;
scanf ("%d%d", &x, &y);
cout << LCA(x, y) << endl;
}
return 0;
}
