知识结构
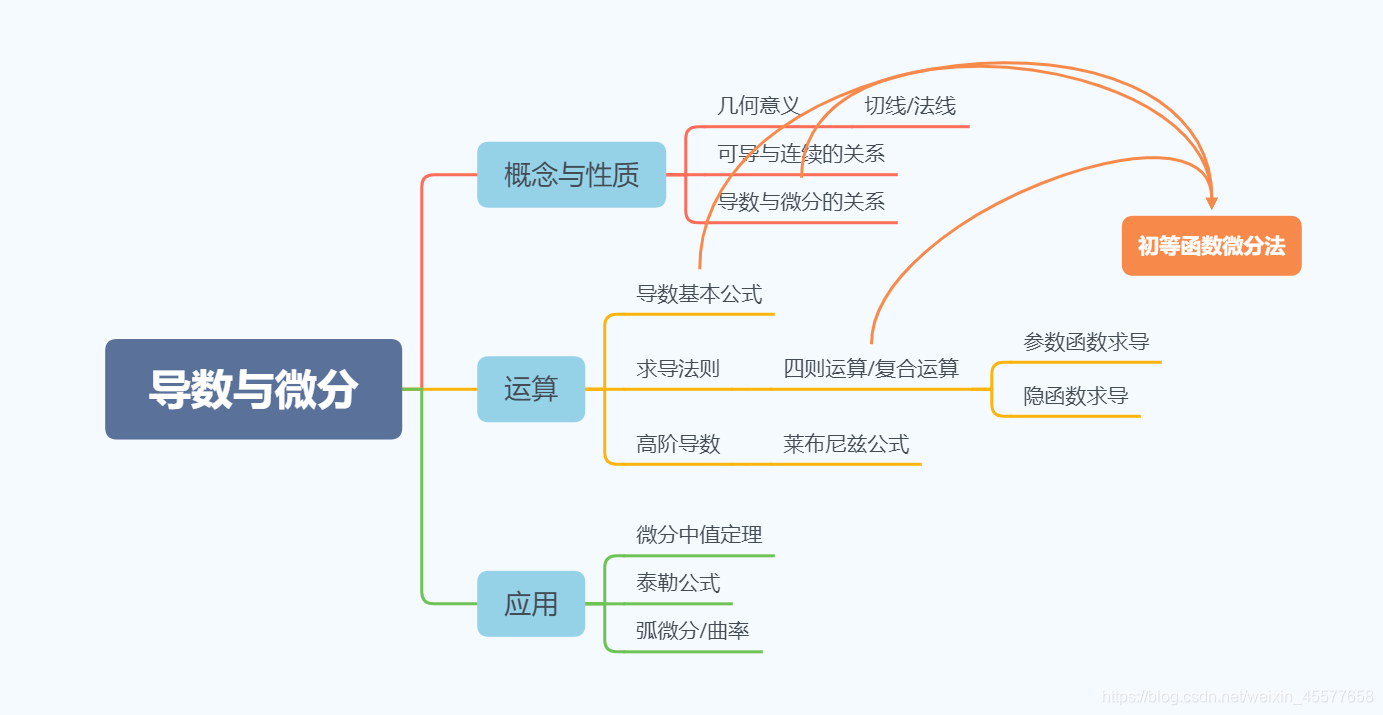
导数、微分的概念与计算
函数的导数与微分分别反映了由自变量的微小变化所引起的函数变化的相对快慢速度(变换率)与绝对变化大小(线性近似)两方面的问题。
函数的常见形式:显函数(包括分段函数、反函数),隐函数,参数式函数以及积分变限函数。
导数的概念
导函数在一点的左极限等于右极限等于函数值。
导函数趋近于这一点的函数值趋近于这一点的函数值。
函数的定积分与极限值都是常数。
函数在一点可导,但是该函数加绝对值后在该点不可导,的充要条件是函数在该点函数值为零,导函数在该点的函数值不为零。
周期函数的导函数也是周期函数且周期不变。
由所给关系式将函数在区间内任一点导函数的定义式转化为在x = 0处的导数的定义式,可得到函数的可导性,找到了导数的关系式,也就是建立了微分方程,解方程就可得到函数表达式。
导数的计算
复合函数求导:求出内外层函数的导数,再相乘即可。内层函数在一点可导是复合函数在一点可导的充分而非必要条件。
分段函数求导:分段点要用定义计算。
若采用逐阶求导的方法计算n阶导数,有时需要对前几阶导数做必要的恒等变形,将他们化为同类型的函数,以利于寻找规律写出一般表达式。必要时可用数学归纳法证明其结论的正确性。
欧拉公式可将实现三角函数和指数函数的互换。在许多演算中处理指数函数更为便捷。
求两个函数的乘积的n阶导数时,若其中一个函数的各阶导数中仅有少数几项不为零,则采用莱布尼兹公式计算较为便捷。
当一个函数在指定点的泰勒展开式比较容易得到时,选用其泰勒级数计算n阶导数是最为简便的。

求有理函数高阶导数的一般方法:如果有理函数是假分式,则利用多项式除法将分式化为多项式与真分式的和,再将真分式拆成分母为一次形式的部分分式(可能是复数系)再求高阶导数。
微分中值定理与导数的应用
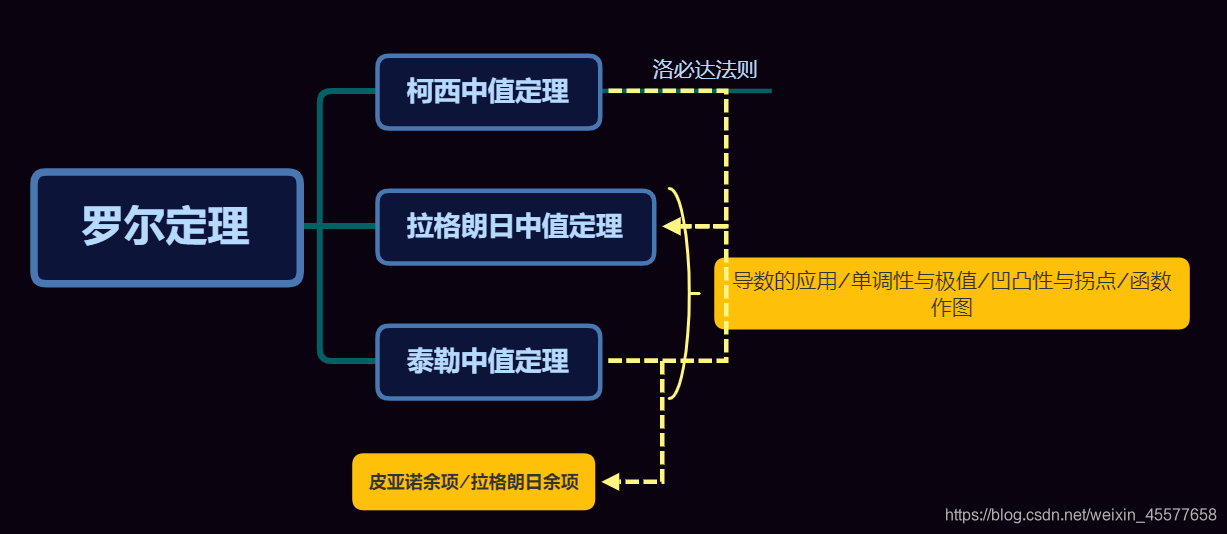
微分中值定理
中值定理的常见应用:证明定理、判断零点、证明等式与不等式、计算极限、判定极值、近似计算等。
带皮亚诺余项的泰勒公式适合于研究函数的局部性态,如极限、极值等情况;带拉格朗日余项的泰勒公式适用于函数的整体性态,如等式,不等式或近似计算等。
用罗尔定理证明等式的常用方法:
将欲证等式写成等号一段只有零,再构造辅助函数。其步骤为:
㈠将f(ξ)= 0改写成f(x) = 0;
㈡依据f(x)构造辅助函数F(x),常用方法是:
①直接观察利用导数的运算法则凑微分;
②利用定积分得到辅助函数;
③解微分方程得到辅助函数。
㈢验证辅助函数在给定区间上满足罗尔定理的条件,便可推出结论。
证明函数零点(方程根)存在性的常用方法是:连续函数的介值定理,罗尔定理。一般首先考虑用介值定理,若函数中含有字母常数不易判断其符号或函数在所讨论的区间中有偶数个零点从而使得函数在两端点处不异号,则用罗尔定理。
证明根的唯一性常用单调性,有多个根的情况常用罗尔定理。
利用微分中值公式证明不等式的方法是:
①根据不等式的特点,选择适当的区间和适当的函数。
②对等式中的导数部分作估计(放大或缩小),得到所证明的结果。
泰勒公式给出了函数值与其各阶导数值之间的关系,当一个命题与函数二阶以及二阶以上的导数有关时,应考虑使用泰勒公式。拉格朗日中值定理是零阶泰勒公式。
导数的应用
证明函数表达式恒为某个常数a的常用方法:
①说明其导数恒为零,在说明该函数在某个指定点的函数值为a;
②说明在指定范围内其最大值和最小值都为a;
③用反证法。
证明不等式的方法:
①利用导数的定义;
②利用微分中值定理;
③利用函数的单调性;
④利用泰勒公式;
⑤利用函数的极值与最值;
⑥利用函数的凹凸性。
