飞行器控制笔记（二）——姿态解算之坐标变换与欧拉角更新姿态

飞行器控制笔记（二）——姿态解算之坐标变换与欧拉角更新姿态

一、基本假定

若将飞行器看作刚体，则它在空间中的姿态主要是指与机体固连的机体坐标系跟与大地固连的坐标系之间的旋转关系。旋转关系可以用欧拉角描述，为了方便叙述，我先记录下面的一些基本假定：
1. 建立的坐标系均是右手系，且欧拉角的旋转方向也满足右手定则；
2. 与机体固连的机体坐标系的$x轴，y轴，z轴$ 的正方向分别为前右下，与大地固连的大地坐标系的$X轴，Y轴，Z轴$ 的正方向分别为北东地；
3. 机体坐标系绕其$z轴$ 旋转所得到的欧拉角称为偏航角$\psi$,机体坐标系绕其$y轴$ 旋转所得到的欧拉角称为俯仰角$\theta$,机体坐标系绕其$x轴$ 旋转所得到的欧拉角称为横滚角$\phi$；
4. 用上下标$b$ 来表示向量在机体（Body）坐标系中，用上下标$e$ 来表示向量在大地（Earth）坐标系中；
5. 在各个坐标系中，与x坐标轴相固连的单位向量$e_1,k_1,n_1,b_1,\ldots=\begin{bmatrix}1&0&0 \end{bmatrix}^T$ ，与x坐标轴相固连的单位向量$e_2,k_2,n_2,b_2,\ldots=\begin{bmatrix}0&1&0 \end{bmatrix}^T$ ，与z坐标轴相固连的单位向量$e_3,k_3,n_3,b_3,\ldots=\begin{bmatrix}0&0&1 \end{bmatrix}^T$。 不论坐标系如何变换，其对应的三个正交单位向量（基底）之间的位置关系并不发生变化，因此才有这个假设。

二、坐标变换矩阵

机体坐标系在任一时刻的姿态都可以分解为通过大地坐标系绕固定点的三次旋转，每次旋转的的旋转轴对应于将要旋转的坐标系的某一坐标轴，也就是上面提到的欧拉角。旋转的次序不同，最终得到的姿态也不相同，因此，这里也规定这三次旋转的次序分别为绕先 $z旋转$ ,再绕$y旋转$,最后绕$x旋转$,即$\psi-\theta-\phi$.如下图所示，机体坐标系的旋转已经分解成了三次坐标系之间基本变换。下面就分别推导绕 $z$ ,绕$y$,绕$x$的坐标变换矩阵。

需要注意到的一点是，这里讨论的都是坐标系之间的变换。也就是说空间中的位置向量或坐标点本身并不发生变化，而只是将它们从一个参考坐标系变换到了另一个参考系当中。

2.1绕z轴旋转

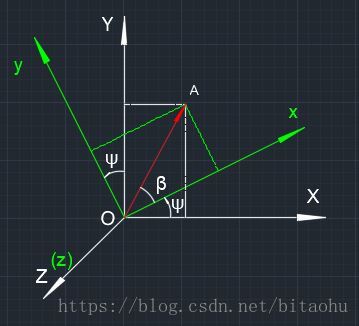
如上图所示，当坐标系绕z轴旋转时，空间中的向量与z轴之间的相对关系不会改变，因此在旋转前后$z\prime=z$,现在就只考虑该向量在垂直于$Z$ 轴的平面上的投影$\vec{OA}$ ，分别在平面直角坐标系$OXY$ 跟平面直角坐标系$Oxy$ 上坐标之间的关系，如果向量$\vec{OA}$ 的模为$r$,它在坐标系$OXY$ 中的坐标可以表示如下：

$$\begin{cases} x=r\cos(\beta+\psi)\\ y=r\sin(\beta+\psi) \end{cases}$$
在坐标系 $Oxy$ 中的坐标如下：
$$\begin{cases} x\prime=r\cos\beta\\ y\prime=r\sin\beta \end{cases}$$
联合这两组式子可以得到：
$$\begin{cases} x\prime&=&x\cos\psi+y\sin\psi\\ y\prime&=&y\cos\psi-x\sin\psi \end{cases}$$
并且已经知道 $z\prime=z$ 了，所以把上面的式子写成矩阵的形式则是：
$$R_z(\psi)=\begin{bmatrix}\cos\psi&\sin\psi&0\\ -\sin\psi&\cos\psi&0\\ 0&0&1 \end{bmatrix}$$
上面这个矩阵就描述了坐标系绕Z轴的一次旋转。

2.2绕y轴旋转

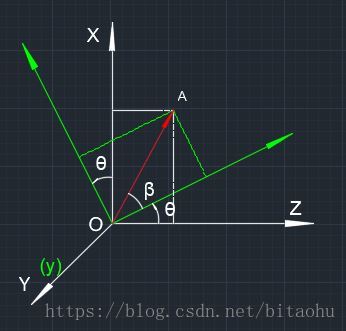
绕y轴旋转的公式推导也与上面是一样的,首先$y\prime=y$,然后向量$\vec{OA}$ 在坐标系$OXY$ 中的坐标可以表示如下：

$$\begin{cases} x=r\sin(\beta+\theta)\\ z=r\cos(\beta+\theta) \end{cases}$$
在坐标系 $Oxy$ 中的坐标如下：
$$\begin{cases} x\prime=r\sin\beta\\ z\prime=r\cos\beta \end{cases}$$
联合这两组式子可以得到：
$$\begin{cases} x\prime&=&x\cos\theta-z\sin\theta\\ z\prime&=&z\cos\theta+x\sin\theta \end{cases}$$
并且已经知道 $y\prime=y$ 了，所以把上面的式子写成矩阵的形式则是：
$$R_z(\psi)=\begin{bmatrix}\cos\theta & 0 & -\sin\theta \\ 0 & 1 & 0 \\ \sin\theta &0 &\cos\theta \end{bmatrix}$$
同样的，上面这个矩阵就描述了坐标系绕Y轴的一次旋转。

2.3绕x轴旋转

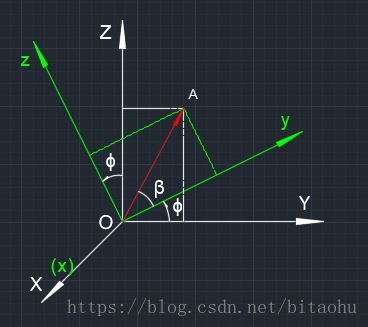
绕x轴旋转的公式推导如下,首先$x\prime=x$,然后向量$\vec{OA}$ 在坐标系$OXY$ 中的坐标可以表示如下：

$$\begin{cases} y=r\cos(\beta+\phi)\\ z=r\sin(\beta+\phi) \end{cases}$$
在坐标系 $Oxy$ 中的坐标如下：
$$\begin{cases} y\prime=r\cos\beta\\ z\prime=r\sin\beta \end{cases}$$
联合这两组式子可以得到：
$$\begin{cases} y\prime&=&y\cos\phi+z\sin\phi\\ z\prime&=&z\cos\phi-y\sin\phi \end{cases}$$
并且已经知道 $x\prime=x$ 了，所以把上面的式子写成矩阵的形式则是：
$$R_z(\psi)=\begin{bmatrix}1 & 0 & 0\\ 0& \cos\phi & \sin\phi \\ 0 & -\sin\phi &\cos\phi \end{bmatrix}$$
同样的，上面这个矩阵就描述了坐标系绕X轴的一次旋转。

扫描二维码关注公众号，回复： 1008128 查看本文章

三 姿态角变化率与机体角速率的关系

有了上面的三个坐标变换矩阵之后，就能很清楚地表示坐标系之间的旋转关系了，但是问题也来了，这三个矩阵有什么用呢，好像跟飞控的姿态解算完全联系不起来。不过注意，每次的旋转过程都是会产生机体姿态角的变化，而飞行器上的陀螺仪可以直接测得机体的角速率，这两个变化率之间似乎关系很明显啊——角速率积分就能得到角度！可是，姿态角的变化率真的就等于机体的角速率吗，这可说不准了，毕竟坐标系本身就发生了改变了的，而且机体的角速率是在机体坐标系下测得的，而姿态角的变化率又是相于大地坐标系的，这两者本来就不是一个东本。下面就记录下这两者关系的推导：

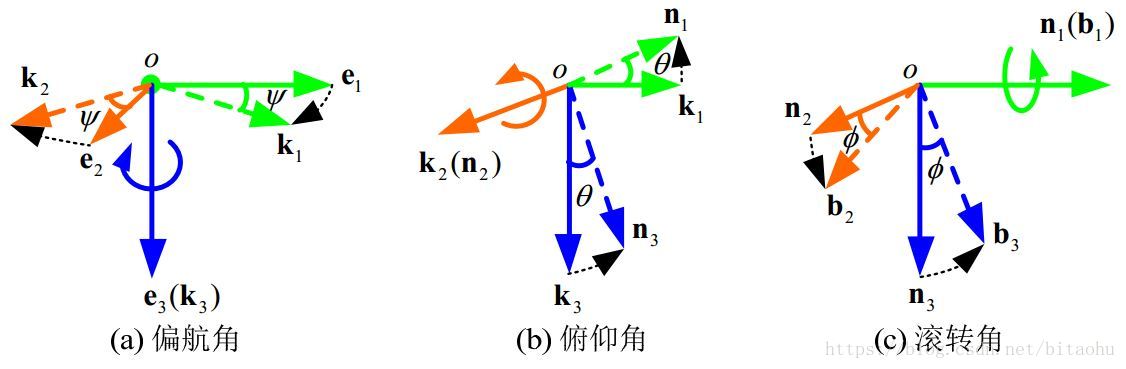
如上图所示，一次完整的旋转被分成了先后三次绕坐标轴的旋转(也可以说其实只存在初始坐标系$oe_1e_2e_3$，和当前坐标系$ob_1b_2b_3$ ,中间出现的两个坐标系都是为了理解方便而假想存在过的。这样说也是合理的，因为对于飞控来说，初始时的坐标系与当前坐标系是真实存在的，也就是陀螺仪相邻两次输出时机体的姿态)。要强调的一点是，在每次绕轴旋转的过程中，旋转轴对应的坐标是不变的，即$k_3=e_3,n_2=k_2,b_1=n_1$.在进行一次完整旋转之后的坐标系$ob_1b_2b_3$中的角速率矢量$^b\omega=\begin{bmatrix} ^b\omega_x&^b\omega_y&^b\omega_z \end{bmatrix}$可以表示成以下的形式：

$$^b\omega=\omega_{xb}\vec{b_1}+ \omega_{yb}\vec{b_2}+\omega_{zb}\vec{b_3}$$
其中 $\omega_{xb}$ 就是当前坐标系 $ob_1b_2b_3$ 绕其x轴即 $b_1$ 向量旋转的角速率 $\psi\prime$
所以，
$$\begin{align} ^b\omega_x&=\phi\prime \vec{b_1} \end{align}$$
也就是，
$$^b\omega_x=\begin{bmatrix} 1&0&0\end{bmatrix}^T\cdot\phi\prime$$
而 $\omega_{yb}$ 则是在上一次绕坐标 $ok_1k_2k_3$ 的y轴即 $k_2$ 向量旋转中的角速率 $\theta\prime$在当前坐标系 $ob_1b_2b_3$ 中的投影。到这里就需要之前所推导的坐标变换矩阵了,绕y轴的旋转对应的变换矩阵就是 $R_y(\theta)$,因此，只要对 $\theta\prime$ 左乘 $R_y(\theta)$ 就可以将俯仰角的变化率变换到当前坐标系 $ob_1b_2b_3$ 中；
$$^b\omega_y= R_y(\theta)\cdot\theta\prime\vec{n_2}$$
也就是,
$$^b\omega_y=\begin{bmatrix} 0&\cos\phi&-\sin\phi \end{bmatrix}^T\cdot\theta\prime$$
同样的，可以说 $^b\omega_z$ 是初始坐标系绕其z轴即 $e_3$ 向量旋转的角速率 $\psi\prime$ 在当前坐标系 $ob_1b_2b_3$ 中的投影，其中先后经过了 $R_y(\theta)-R_x(\phi)$ 两次坐标变换，也就是先对 $e_3$ 向量左乘 $R_y(\theta)$ 再左乘 $R_x(\phi)$,即：
$$^b\omega_z=R_x(\phi)\cdot R_y(\theta) \cdot\psi\prime \vec{k_3}$$
也就是，
$$^b\omega_z=\begin{bmatrix} -\sin\theta & \cos\theta\sin\phi & \cos\theta\cos\phi \end{bmatrix}^T\cdot \psi\prime$$
结合上面的式子，可以得到：
$$\begin{bmatrix} ^b\omega_x \\^b\omega_y \\ ^b\omega_z \end{bmatrix}=\begin{bmatrix} 1&0&-\sin\theta\\0&\cos\phi&\cos\theta\sin\phi\\o&-\sin\phi&\cos\theta\cos\phi \end{bmatrix}\cdot\begin{bmatrix} \phi\prime \\ \theta\prime \\ \psi\prime \end{bmatrix}$$
可以看出，这个式子用姿态变化率来表示角速率，离最终的目标就差一点了，只需要进行简单的将矩阵除过去，就可以得到通过角速率表示姿态变化率的式子了：
$$\begin{bmatrix} \phi\prime \\ \theta\prime \\ \psi\prime \end{bmatrix}=\begin{bmatrix} 1&\tan\theta\sin\phi&\tan\theta\cos\phi \\ 0&\cos\phi &-\sin\phi \\ 0&\frac{\sin\phi}{\cos\theta} & \frac{\cos\phi}{\cos\theta} \end{bmatrix}\cdot\begin{bmatrix} ^b\omega_x \\^b\omega_y \\ ^b\omega_z \end{bmatrix}$$
到这一步，离解算出机体姿态的目标基本就已经达到了，用上一篇里提到的数值计算方法就可以来求解这组微分方程了，从而得到每个时刻的姿态，并且当俯仰与横滚角比较小时，姿态变化率与机体角速率近似相等，因此，如果姿态变化不大，姿态角度可以直接用角速率积分得到。这种使用直接使用欧拉角来更新姿态的方法物理意义直观明显，但是由于需要计算较多的三角函数，因此计算量较大，而且当俯仰角 $\theta$ 接近 $\pm90^\circ$ 时，矩阵中的 $\cos\theta$ 会等于0，这会导致出现奇异性问题。这是欧拉角描述旋转本身存在的一个缺陷，即万向节死锁现象，所以这种方法在飞控当中用得不多，至少我没有看到过。此外，可以发现，其实这三个欧拉角之间并不是独立的，而是相互有耦合关系的。

参考文献

1. 高强，王力，侯远龙，童仲志，陈机林.火控系统设计概论，北京：国防工业出版社，2016
2. 全权.多旋翼飞行器设计与控制，北京：电子工业出版社