模拟退火算法细讲-分享给过几天参加建模比赛的你

模拟退火

算法简介

模拟退火算法是一种基于蒙特卡洛思想设计的近似求解最优化问题的方法。
它是一种适合解大规模组合优化问题的通用有效近似算法，是局部搜索算法的扩展，从理论上来说它是一个能求得全局最优化结果的算法，它是一种启发式算法，源于对固体退火的研究。它是利用问题的求解过程与融化物体退火过程的相似性，采用随机模拟物体退火过程来完成问题的求解，也就是在控制温度的作用下对参数的值进行调整，知道所选取的参数值最终使能量函数(目标函数)达到全局最小值。

思想

既然模拟退火算法思想源于固体退火，那我们简单了解一下固体退火。

• 退火：退火是指将固体加热到非常高的温度之后，让其中的分子成随机排列状态，然后以一定的速率逐步降温，其中在降温的过程中每个状态下分子都会随机运动，因此在这个过程中会出现很多种不同的排列状态，当固体缓慢冷却之后分子往往能以低能状态排列，使得固体内部达到内能最小的稳定状态。

因此类别固体退火，模拟退火就是指从某一初始温度开始，让温度以某一适宜速率缓慢下降，同时结合概率突跳特性在目标函数的解空间内随机寻找全局最优解。
模拟退火算法和其它的搜索算法相比有一些特点：

• 1.以一定的概率接受恶化解。

我们知道，一些传统的随机搜索算法往往在搜索过程中只接受是目标函数解**变“好”**的解，这样在很多情况下总会不可避免的陷入局部最优解，而对模拟退火而言，它会以一定的概率接受恶化解，使得它具有更强的灵活性，可以跳出局部最优解。

如上图，假设图中的蓝色曲线为目标函数，当用模拟退火算法搜索最优解时，假设初始点为A，在搜索过程中它可能很容易就搜索到了C点，但显然这只是个局部最优解，能够以一定概率接受恶化解的选择使得它将可能跳出这个局部最优解进而继续搜索到全局最优G点。

• 2.引进了算法控制参数

模拟退火引入了类似于退火温度的算法控制参数，它将优化过程分为几个阶段，并决定各个阶段下的取舍标准，它依据的是Metroplis准则，具体来说是什么意思呢，我们看一下Metroplis准则公式：

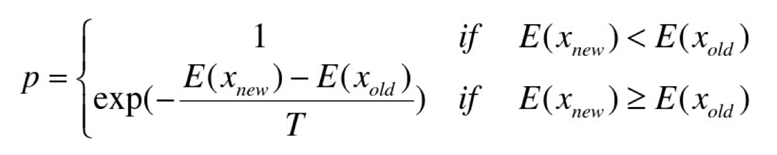
其中，Xnew为得到的新解，Xold为当前解，E()为目标函数法则，上面这个公式是什么意思呢？简单来说，**就是在某个温度下固体分子从一个状态转移到另一个状态时(后面会讲到某个温度下转移状态的次数为马尔科夫链的长度，也就是每个温度下不止有一个状态)，如果新状态的内能小，则无条件直接接受新解，而如果新状态的内能小，则以一定概率接受它。这个一定概率满足的条件就是指图中的那个公式。**经过对这个公式的分析我们发现，当新解没有当前解好的时候，接受的概率主要跟两解的差值和当前温度有关，我们来分析一下，假如当前温度是固定的，那么差值越小那么加上负号的分子就越大，总体接受的概率就越大，假如差值一定，那么当前温度越小，分数越大，加上符号就越小，总体接受的概率就越小，也就是说，差值越小我越可能接受你，而当前温度越高，我可以搜索的时间就比较充裕也越可能接受新解，当前温度越低，就越接近算法的搜索上限了，快要停止搜索了，我就尽可能保证不接受恶化解。大致就是这么个意思哈哈。

• 3.使用对象函数值进行搜索

传统搜索算法往往在使用目标函数的前提下还需要额外使用目标函数的导数值等一些其它辅助信息才能确定搜索方向，如果辅助信息很少或者没有，那么算法就失效了，而模拟退火仅使用目标函数转换来的适应度函数值，就可以确定搜索方向和范围。

• 4.隐含并行性

并行性往往能够提高一个算法的效率，而将模拟退火改造成并行算法还是比较容易的，如可以使用操作并行策略、试演并行策略、区域分裂策略和混乱松弛策略等，这些改造在不同程度上对解的质量、收敛速度上比模拟退火更优，这部分内容比较深入，想了解的小伙伴可以自行了解，本文不再介绍。

算法步骤

初始化参数

在模拟退火算法中有一系列的参数需要我们自行设置，如

• 1.初始温度
• 2.初始解
• 3.马尔科夫链的长度
• 4.控制温度衰减的函数参数
• 5.算法停止温度

1 其中初始温度就是降温开始的温度，一般要求它足够高，但实际上问题规模不同它的需求也不同，这要根据实际问题进行分析处理，实在不行多试几下就好了。
2 初始解指算法开始运行的最开始的解，对模拟退火算法而言初始解的设定对最终搜索结果影响不大，因此这个用随机函数什么的设置一个即可，但是对有些算法比如遗传算法，就可能需要找到尽可能好的初始解，因此它经常和神经网络进行结合使用进行算法优化。
3 马尔科夫链的长度也就是指任意温度下的迭代次数，算法在马尔可夫链的长度内持续进行产生新解、判断、接受/舍弃的迭代过程。
4 控制温度衰减的函数参数也成为退火策略。我们往往需要温度以适当的方式进行降温，降温越快搜索的解空间越小越不容易找到最优解，降温越慢越影响算法效率，实际上我们往往使用两种方法进行温度衰减:

t(k+1) = a*t(k)
t(k) = (L-k)/L - t ,k=1,2,3…

对于第一种方法，a为一个接近1的常数，一般取0.5-0.99，比较好理解，就是根据前一温度依次下降一点。
对于第二中方法，L为算法控制参数下降的总次数，也就是马尔科夫链的长度，也是以一定规律下降的。
5 算法停止温度即当温度下降到此时算法搜索停止，采用当前最优解为全局近似最优解。

实际上，经过算法的理解我们应该知道了，设置的初始温度尽量足够高，马尔可夫链迭代次数尽量足够大，终止温度进行足够低，降温过程尽量足够缓慢，这样的设置我们更可能保证获得全局最优解，但在使用过程中肯定要平衡好效率来设置参数，使得算法效率更好。

产生新解

产生新解是由一个产生函数从当前解产生一个位于解空间的新解，一般是从当前解进行扰动产生的，为便于后续的计算和接受，减少算法耗时，通常选择由当前新解经过简单地变换即可产生新解的方法，如对构成新解的全部或部分元素进行置换、互换等。因为模拟退火能解决的问题有很多种，这个要根据具体问题进行分析选择。

判断新解是否接受

这一步就根据前边的 Metroplis准则进行判断选择了。

循环

即在某一温度下，重复马尔可夫链长度的扰动和接受过程，即不断产生新解并判断是否接受

降温

每次循环过后按照降温的函数来进行降温，就这样不断降温，不断循环迭代。

找到最优解

在温度降到我们设置的终止温度后算法停止搜索，采用当前最优解为全局近似最优解，算法结束。

算法实现流程图

实例及代码

算法学的差不多了，那怎么能不看个实例和相关代码呢，下面给出一个TSP问题的实际例子及其求解代码，很多地方都已经注释了，如果有不懂的同学可以私信我哦。
问题：一旅行小伙想去国内34个城市旅游，要求一次走完不重复且走的总距离最短，有已知的34个城市的经纬度，求最短总距离。

clc;clear;      %清空工作区及命令行
data=[116.28,39.54; 121.29,31.14; 117.11,39.09; 106.32,29.32; 126.41,45.45;
        125.19,43.52; 123.24,41.50; 111.48,40.49; 114.28,38.02; 112.34,37.52;
        117.00,36.38; 113.42,34.48; 108.54,34.16; 103.49,36.03; 106.16,38.20;
        101.45,36.38;  87.36,43.48; 117.18,31.51; 118.50,32.02; 120.09,30.14;
        113.00,28.11; 115.52,28.41; 114.21,30.37; 104.05,30.39; 106.42,26.35;
        119.18,26.05; 113.15,23.08; 110.20,20.02; 108.20,22.48; 102.41,25.00;
         90.08,29.39; 114.10,22.18; 113.35,22.14; 121.31,25.03];        
%data为经纬度矩阵，第一列为经度，第二列为纬度
lon = data(:,1);    %lon为经度矩阵
lat  = data(:,2);    %lat为纬度矩阵
picture=plot([lon;lon(1)],[lat;lat(1)],'.r-','markersize',15); 
lon = (lon/180)*pi;   %将经纬度化为弧度制便于利用公式求距离
lat  = (lat/180)*pi;
len = size(lon,1)   %得到城市的数量
Distance = zeros(len) %产生len*len的0矩阵用来存放各个城市的距离
R = 6378.137   %地球半径
for i =1:len
    for j = 1:len
        Dlon = lon(i)-lon(j);
        Dlat  = lat(i)-lat(j);
        Distance(i,j)=2*R*asin(sqrt(sin(Dlat/2)^2+sin(Dlon/2)^2*cos(lat(i))*cos(lat(j))));
    end   %上面这一长串是用的公式计算两城市的距离并存在距离矩阵中
end
%下面开始初始化参数
T0 = 2000; %初始温度
T = 1;    %终止温度
a = 0.99;    %温度衰减系数
n = len;   %n为城市总数量，为了程序更清晰新赋值一个变量
L = 100*n;  %马尔可夫链的长度
path = randperm(n); %产生初始路径，这个函数是将1-34随机排列成一维矩阵，我们将其作为初始解
Dpath = 0;   %Dpath为初始解的路线长度
for i = 1:n-1
    Dpath = Dpath+Distance(path(i),path(i+1));
end
Dpath = Dpath + Distance(path(n),path(1));%初始解的长度为此
while T0>T        %降温过程
    for i = 1:L       %马尔可夫链迭代过程
        value1 = ceil(n*rand);
        value2 = ceil(n*rand);
        val1 = min(value1,value2);
        val2 = max(value1,value2);
        pathvalue = fliplr(path(val1:val2));%fliplr是一个逆置函数，将两参数之间数逆置
        newpath = [path(1:(val1-1)),pathvalue,path((val2+1):n)];%这就是新产生的路径矩阵
        newDpath = 0;
        for i = 1:n-1
            newDpath = newDpath+Distance(newpath(i),newpath(i+1));
        end
            newDpath = newDpath + Distance(newpath(n),newpath(1));
            %newDpath是新产生的路径的总长度
            if newDpath<Dpath  %如果新路径比原路径小，直接接受
                path = newpath;
                Dpath = newDpath;
            elseif exp((Dpath-newDpath)*2/T0)>rand %如果新路径比原路径大，以一定概率接受
                path = newpath;
                Dpath = newDpath;
            else            %负责路径不改变
                path = path;
                Dpath = Dpath;
            end
    end
    T0 = a*T0;
    set(picture,'xdata',lon([path path(1)]),'ydata',lat([path path(1)]));
    xlabel(sprintf('总距离=%.1f',Dpath),'fontsize',10);
    title(sprintf('当前温度T=%.1f',T0),'fontsize',10);
    drawnow;
end

最后注意一点，因为CSDN不支持Matlab代码块显示，我用的Java代码块，原语句中的注释为%我并没有改变，为的是保证大家复制粘贴即可运行观看结果。
值得一提的是，有时候在解决问题的时候需要的不仅仅是最终的解，掌握好的作图方法能将结果给完美的展示出来也非常重要，我写过一篇Matlab绘图方法的博文，有兴趣的大家可以参考一下：
Matlab绘图方法整理(超完整版)

最终，非常感谢你能看到这里，如果觉得文章对你有帮助，不妨点个赞哟，祝大家学业有成、工作顺利！