Por qué los filtros ideales no son realizables

La función del sistema en la señal se puede dividir aproximadamente en dos categorías: una es la transmisión de la señal y la otra es el filtrado. La transmisión de señales requiere que la señal no se distorsione tanto como sea posible, mientras que el filtrado requiere filtrar o debilitar los componentes no deseados, lo que inevitablemente va acompañado de distorsión. A continuación, este artículo presentará el filtrado de la señal de la transmisión sin distorsión de la señal y luego explicará en detalle por qué no se puede realizar el filtro ideal.

1. Transmisión sin distorsiones

Presumiblemente, todos conocen el juego de relevos, a menudo la expresión final será muy diferente de la expresión original, es decir, se producirá una distorsión que debe evitarse en el proceso de transmisión de la señal.

1.1 Definición

La transmisión de señal sin distorsión significa que, en comparación con la señal de entrada, la señal de salida del sistema solo es diferente en la magnitud de la amplitud y la secuencia del tiempo de aparición, pero no hay cambio en la forma de onda.

Es decir, la forma de la señal de salida debe ser una combinación de la señal de entrada después de la transformación de estiramiento o compresión más la transformación de traducción. La ventaja de esto es que la señal original se puede restaurar fácilmente en el extremo de salida de la señal. Para dar un ejemplo específico, si la señal de entrada es $f\left(t\right)$ , la salida después de pasar por el sistema de transmisión es$y\left(t\right)$ , si el sistema es un sistema de transmisión sin distorsión,$La\; relación\; que\; deben\; satisfacer\; f\left(t\right)ey\left(t\right)$ es aproximadamente la siguiente:

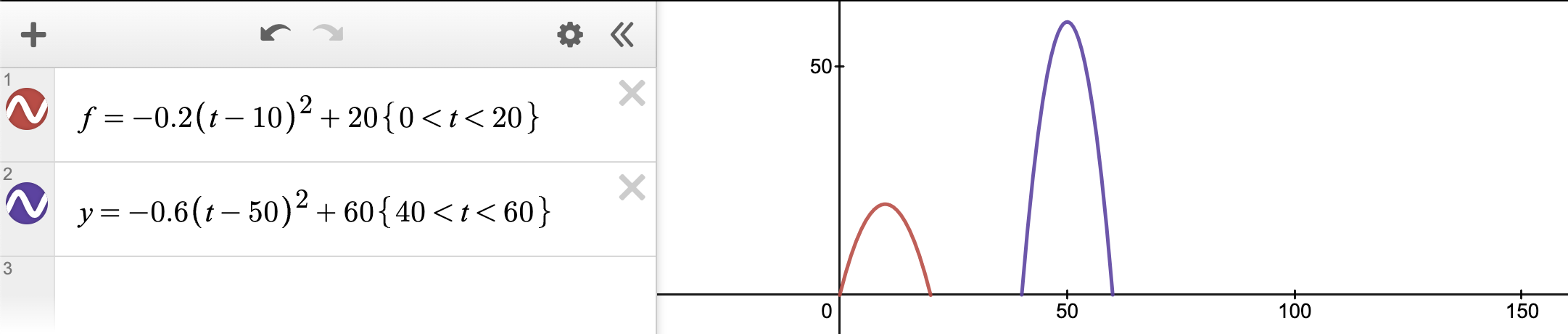
Si se utiliza una expresión matemática estricta para describir la señal de entrada $f\left(t\right)$ y señal de salida$La\; relación\; de\; y\left(t\right)$ es:
$$y\left(t\right)=Kf\_\left(t-t_{}\right)$$
realizan respectivamente la transformada de Fourier en ambos lados del signo igual y, de acuerdo con las características de cambio de tiempo de la transformada de Fourier, obtienen la relación espectral de entrada y salida:
$$Y\left(j\omega \right)=k{e}^{-j\omega t_{}}F\left(j\omega \right)$$

1.2 Condiciones de transmisión sin distorsión

Respuesta al impulso del sistema $h\left(t\right)$的要求：
$$h\left(t\right)=K\delta \_\left(t-t_{}\right)$$
a la función de transferencia del sistema (función de respuesta de frecuencia)H ( j ω ) H(j\omega)Defina$H$$($$j$$\omega$$)$
$$\begin{array}{c}H\left(j\omega \right)=Y\left(j\omega \right)/F\left(j\omega \right)=k{e}^{-j\omega t_{}}\\ \text{Ahora mismo}|H(j\omega )\_=K,yo(o)=-t\_{\_}_{}\end{array}$$
Por lo tanto, bajo la condición de transmisión sin distorsiones, las características de amplitud-frecuencia del sistema $|H(j\omega )|$ y características de frecuencia de fase$\theta \left(\omega \right)$ debería verse así:

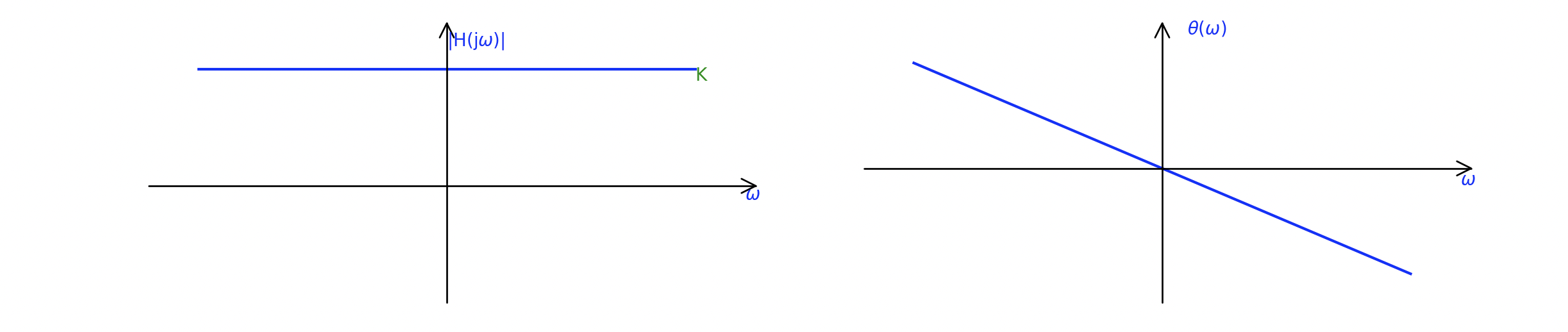
Cabe señalar que las condiciones anteriores son condiciones ideales para la transmisión de señales sin distorsión. Al transmitir una señal con un ancho de banda limitado, siempre que las características de amplitud-frecuencia y fase-frecuencia del sistema cumplan con las condiciones anteriores dentro de la banda de frecuencia ocupada por la señal. Por ejemplo, si queremos transmitir la señal de voz del habla humana, siempre que esté dentro de los 20000 Hz, las características de amplitud-frecuencia del sistema de transmisión ∣ H ( j ω $|H(j\omega )|$ y características de frecuencia de fase$\theta \left(\omega \right)$ debe cumplir los requisitos anteriores.

2. Filtro de paso bajo ideal

Si el filtro se considera como un sistema, como sugiere su nombre, el papel del filtro de paso bajo ideal debería ser: superior a una determinada frecuencia f C f_C set$F_{}$Los componentes de forma de onda de se filtrarán de la señal original. La frecuencia establecida $F_{}$se denomina frecuencia de corte, y su frecuencia angular de corte correspondiente se registra como ${Vaya}_{}=2\pi f_{}$, la característica de amplitud-frecuencia del sistema∣ $|H(j\omega )|$ y características de frecuencia de fase$\theta \left(\omega \right)$ debería verse así:

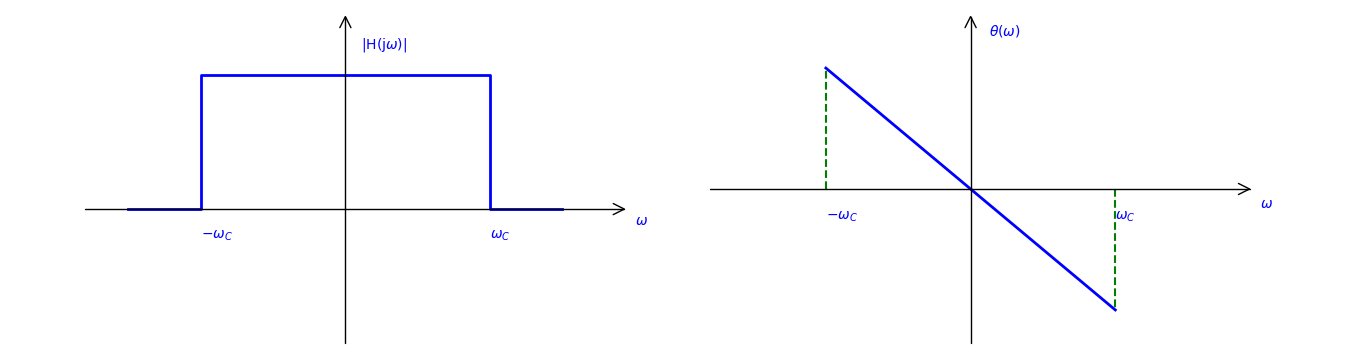
Entonces, la función de respuesta de frecuencia del filtro de paso bajo ideal $Defina\; H\left(j\omega \right)$ como:
$$H\left(j\omega \right)=\{\begin{array}{cl}{mi}^{-j\omega t_{}},& |\omega |<{Vaya}_{}\\ 0& |\omega |>{Vaya}_{}\end{array}={gramo}_{2o_{}}(o){mi}^{-j\omega t_{}}$$
Entre ellos, ${gramo}_{2o_{}}\left(\omega \right)$ indica que la variable independiente es$oh$ ,$0$ como el centro, con$2o_{}$es el ancho de la función de puerta.

Entonces, la respuesta de impulso del filtro de paso bajo ideal $h\left(t\right)$为：
$$\begin{array}{rl}h\left(t\right)& =F^{-1}\left[{gramo}_{2o_{}}\left(o\right){mi}^{-j\omega t_{}}\right]\\ & =\frac{{Vaya}_{}}{Pi}sa\_[{ay}_{}\left(t-t_{}\right)\end{array}$$
El proceso de cálculo anterior puede referirse al proceso de solución de la transformada de Fourier de la función de puerta en el artículo "Realmente dominar la transformada de Fourier", y luego se puede obtener fácilmente de acuerdo con la simetría de la transformada de Fourier.

Frecuencia angular de corte ${Vaya}_{}=5$ , cambio de hora$t_{}=Cuando\; 1$ , la respuesta de impulso del filtro de paso bajo ideal correspondiente se muestra en la siguiente figura:

Verás, cuando la entrada es la función de impulso $\delta \left(t\right)$ , la respuesta de impulso de este filtro$h\left(t\right)$ en realidad requiere que una parte de ella exista antes de la entrada ($t<0$ ), lo que viola la causalidad, por lo que es imposible decir que este es un filtro de paso bajo ideal.

Desde el punto de vista de la transmisión de señales, cuando el sistema de transmisión es un filtro de paso bajo ideal, la señal de impulso $\delta \left(t\right)$ se distorsiona en la respuesta de impulso de un filtro de paso bajo ideal$h\left(t\right)$ parece. Esto se debe a que$La\; banda\; de\; frecuencia\; de\; la\; señal\; de\; \delta \left(t\right)$ es infinitamente amplia, mientras que la banda de paso de un filtro de paso bajo ideal es limitada.

3. Condiciones para sistemas físicamente realizables

Hay dos condiciones necesarias para que un sistema sea físicamente realizable, la primera condición es una condición causal, es decir, un sistema causal es un sistema físicamente realizable. La definición de un sistema causal es: la respuesta de estado cero no aparecerá en el sistema antes de la excitación, expresada como:
$$h\left(t\right)=0,t<0$$
es fácil de entender, por ejemplo, si queremos grabar una oración en un papel en blanco, es imposible que se dé esta situación: estamos a punto de tomar un bolígrafo y la oración ya está escrita a la mitad; vamos a la cafetería a comer, y estamos listos para comer Antes, parte de la comida ya había entrado en el estómago.

La segunda condición necesaria es la función de transferencia $H\left(j\omega \right)$要要成佩利-维纳电影：
{ ∫ − ∞ ∞ ∣ H ( j ω ) ∣ 2 re ω < ∞ ∫ − ∞ ∞ ∣ ln ⁡ ∣ H ( j ω ) ∣ ∣ / ( 1 + ω 2 ) re ω < ∞ \begin{casos} \int_{-\infty}^{\infty}|H(j \omega)|^{2} d \omega<\infty\\ \\ \int_{ - \infty}^{\infty} \big|\ln| H(\mathrm{j} \omega)|\big|/({1+\omega^{2}}) \mathrm{~d} \omega<\infty \end{casos}⎩⎪⎨⎪⎧∫− ∞∞∣ H ( j ω ) _2 reω<∞∫− ∞∞∣∣en∣ H ( j ω ) _∣∣/ ( 1+Vaya2 )reω <∞
Esto muestra que para que el sistema sea físicamente realizable, es posible permitir $La\; característica\; H\left(j\omega \right)$ es 0 en algunos puntos de frecuencia discontinuos, pero no se permite que sea 0 en una banda de frecuencia limitada (porque$Cuando\; H\left(j\omega \right)$ es 0, la parte molecular $ \big|\ln | H(\mathrm{j} \omega)|\big|$ del integrando de la segunda fórmula anterior es infinita). De acuerdo con este principio, los filtros ideales como el paso bajo ideal, el paso alto ideal, el paso de banda ideal y el supresor de banda ideal son todos irrealizables.

Nota: este artículo se publicó por primera vez en la cuenta pública de WeChat " Instituto de investigación de señales de vibración "