Directorio de artículos
1. Definición de transformada de Fourier y transformada de Laplace
1. Integral de Fourier
Teorema de la integral de Fourier Si f ( t ) f(t)f ( t ) en( − ∞ , + ∞ ) (-\infty,+\infty)( -∞ , _+ ∞ ) satisface las siguientes condiciones:
(1)f ( t ) f(t)f ( t ) satisface la condición de Dirichlet en cualquier intervalo finito (continuo o solo un número limitado de puntos discontinuos del primer tipo; solo un número limitado de puntos extremos); (2)
f( t ) f(t)f ( t ) en el intervalo infinito( − ∞ , + ∞ ) (-\infty,+\infty)( -∞ , _+ ∞ ) es absolutamente integrable (es decir, la integral∫ − ∞ + ∞ ∣ f ( t ) ∣ dt \int_{-\infty}^{+\infty}|f(t)|\mathrm{d}t∫− ∞+ ∞∣ f ( t ) ∣ d t ecuación), y si f ( t ) = 1 2 π ∫ − ∞ + ∞ [ ∫ − ∞ + ∞ f ( τ ) e − i ω τ re τ ] ei ω td ω f( t)=\frac{1}{2\pi }\int_{-\infty}^{+\infty}\left[\int_{-\infty}^{+\infty} f(\tau)e^{ -i\omega\tau}\mathrm{d}\tau\right]e^{i\omega t}\mathrm{d}\omegaf ( t )=14:00 _1∫− ∞+ ∞[ ∫− ∞+ ∞f ( τ ) mi- yo ω τ reτ]miiω t dωf ( t ) f(t)a la izquierdaf ( t ) debe ser f ( t + 0 ) + f ( t − 0 ) 2 \frac{f(t+0)+f(t-0)}{2}en su punto de discontinuidad2f ( t + 0 ) + f ( t − 0 )(valores medios extremos izquierdo y derecho) en su lugar.
2. Transformada de Fourier
Transformada de Fourier : si f ( t ) f(t)f ( t ) en( − ∞ , + ∞ ) (-\infty,+\infty)( -∞ , _+ ∞ ) satisfacen las condiciones de la integral de Fourier, entonces la función F ( ω ) = F [ f ( t ) ] = ∫ − ∞ + ∞ f ( t ) e − i ω tdt F(\omega)=\mathscr {F }[f(t)]=\int_{-\infty}^{+\infty}f(t)e^{-i\omega t}\mathrm{d}tF ( ω )=F [ f ( t )]=∫− ∞+ ∞f ( t ) mi− yoω t retesf ( t ) f(t)La transformada de Fourier de f ( t ) y la función f ( t ) = F − 1 [ F ( ω ) ] = 1 2 π ∫ − ∞ + ∞ F ( ω ) ei ω td ω f(t)=\ mathscr {F}^{-1}[F(\omega)]=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F(\omega)e^{i\ omega t}\mathrm{d}\omegaf ( t )=F− 1 [F(ω)]=14:00 _1∫− ∞+ ∞F ( ω ) miyoω t reωφF(ω ) F(\omega)Transformada inversa de Fourier de F ( ω ) .
3. Función de impulso unitario y función de escalón unitario
Función de impulso unitario : δ ( t ) = { + ∞ , t = 0 0 , t ≠ 0 \delta(t)=\begin{cases} +\infty,&t=0\\ 0,&t\ne 0 \end{ casos}re ( t )={ + ∞ ,0 ,t=0t=0Esta es una declaración imprecisa, y una declaración rigurosa requiere el uso de límites débiles. Esta función satisface ∫ − ∞ + ∞ δ ( t ) dt = 1 \int_{-\infty}^{+\infty}\delta(t)\mathrm{d}t=1∫− ∞+ ∞δ ( t ) re t=1 Sif ( t ) f(t)f ( t ) es una función infinitamente diferenciable, entonces existe ∫ − ∞ + ∞ δ ( t ) f ( t ) dt = f ( 0 ) \int_{-\infty}^{+\infty}\delta(t ) f(t)\mathrm{d}t=f(0)∫− ∞+ ∞δ ( t ) f ( t ) re t=f ( 0 ) δ ( t ) \delta(t)δ ( t ) es una función par, que satisfaceδ ( at ) = 1 ∣ a ∣ δ ( t ) \delta(at)=\frac{1}{|a|}\delta(t)δ ( un t )=∣ un ∣1δ ( t )(un ≠ 0 un\no 0a=0),且∫ − ∞ + ∞ δ ( norte ) ( t − t 0 ) f ( t ) dt = ( − 1 ) nf ( norte ) ( t 0 ) \int_{-\infty}^{+\infty} \delta^{(n)}(t-t_0)f(t)\mathrm{d}t={(-1)}^nf^{(n)}(t_0)∫− ∞+ ∞d( n ) (t−t0) f ( t ) re t=( -1 ) _norte f( n ) (t0) (esto se demuestra por integración por partes). En particular,∫ − ∞ + ∞ δ ′ ( t ) f ( t ) dt = − f ′ ( 0 ) \int_{-\infty}^{+\infty}\delta'(t)f(t)\mathrm {d}t=-f'(0)∫− ∞+ ∞d′ (t)f(t)ret=- f′ (0)
Función escalón unitario : u ( t ) = { 1 , t > 0 0 , t < 0 u(t)=\begin{cases} 1,&t>0\\ 0,&t<0 \end{cases}tu ( t )={ 1 ,0 ,t>0t<0成动∫ − ∞ t δ ( τ ) re τ = tu ( t ) ddtu ( t ) = δ ( t ) \int_{-\infty}^t\delta(\tau)\mathrm{d}\tau=u ( t)\\ \frac{\mathrm{d}}{\mathrm{d}t}u(t)=\delta(t)∫− ∞tre ( t ) re t=tu ( t )dt _retu ( t )=re ( t )
4. Transformada de Laplace
Transformada de Laplace : Sea la función f ( t ) f(t)f ( t )在t ≥ 0 t\ge 0t≥0 está definido y la integral∫ 0 + ∞ f ( t ) e − stdt \int_0^{+\infty}f(t)e^{-st}\mathrm{d}t∫0+ ∞f ( t ) mi− s t dten el plano complejossLa convergencia en un área determinada de s , entonces se llama F ( s ) = L [ f ( t ) ] = ∫ 0 + ∞ f ( t ) e − stdt F(s)=\mathscr{L}[f (t)] =\int_0^{+\infty}f(t)e^{-st}\mathrm{d}tF ( s )=L [ f ( t )]=∫0+ ∞f ( t ) mi- s t retesf ( t ) f(t)La transformada de Laplace (o función imagen) de f ( t ) se llama f ( t ) f(t)f ( t ) esF ( s ) F(s)La transformada inversa de Laplace de F ( s ) (o llamada función original), registrada como f ( t ) = L − 1 [ F ( s ) ] f(t)=\mathscr{L}^{-1 }[F (s)]f ( t )=L− 1 [F(s)]edad jovens = β + yo ω s=\beta+i\omegas=b+iω ,则L [ F ( t ) ] = F [ F ( t ) tu ( t ) mi − β t ] \mathscr{L}[f(t)]=\mathscr{F}[f(t)u( t)e^{-\beta t}]L [ f ( t )]=F [ f ( t ) tu ( t ) mi- βt ]. Esta es la relación entre la transformada de Laplace y la transformada de Fourier.
El teorema de existencia de la transformada de Laplace Si la función f ( t ) f(t)f ( t ) satisface las siguientes condiciones:
(1) Ent ≥ 0 t\ge 0t≥0 continuo o continuo a trozos en cualquier intervalo finito;
(2) cuandot → + ∞ t\to+\inftyt→+ ∞ ,f ( t ) f(t)La tasa de crecimiento de f ( t ) no supera una determinada función exponencial, es decir, existeM > 0 M>0METRO>0和c ≥ 0 c\ge 0C≥0使得∣ f ( t ) ∣ ≤ METRO ect , ∀ t ∈ [ 0 , + ∞ ) |f(t)|\le Me^{ct},\forall t\in[0,+\infty)∣ f ( t ) ∣≤yo _c t ,∀ t∈[ 0 ,+ ∞ ) entoncesf ( t ) f(t)Transformada de Laplace de f ( t ) F ( s ) = ∫ 0 + ∞ f ( t ) e − stdt F(s)=\int_0^{+\infty}f(t)e^{-st}\ mathrm{d }tF ( s )=∫0+ ∞f ( t ) mi− s t reten el semiplanoRe ( s ) > c \operatorname{Re}(s)>cRe ( s )>Debe existir en c , y la integral de la derecha está enRe ( s ) ≥ c 1 > c \operatorname{Re}(s)\ge c_1>cRe ( s )≥C1>Absolutamente convergente y uniformemente convergente en c , y en Re ( s ) > c \operatorname{Re}(s)>cRe ( s )>En el semiplano de c ,F ( s ) F(s)F ( s ) es una función analítica. CCc se llamaf ( t ) f(t)El exponente de crecimiento de f ( t ) .
2. Transformada de Fourier y transformada de Laplace de funciones comunes
| Como función primitiva f ( t ) f(t)f ( t ) | Transformada de Fourier | Transformada de Laplace |
|---|---|---|
| 1 11 | 2 π δ ( ω ) 2\pi\delta(\omega)2 p d ( o ) | - |
| δ ( t ) \delta(t)re ( t ) | 1 11 | 1 11 |
| tu (t) tu(t)tu ( t ) | 1 yo ω + π δ ( ω ) \cfrac{1}{i\omega}+\pi\delta(\omega)yo1+pd ( o ) _ | 1 s \cfrac{1}{s}s1 |
| tnt^ntnorte | 2 π en δ ( norte ) ( ω ) 2\pi i^n\delta^{(n)}(\omega)2 π yonorte _( n ) (o) | Γ ( norte + 1 ) s ( norte + 1 ) ( norte > − 1 ) \cfrac{\Gamma(n+1)}{s^{(n+1)}}(n>-1)s( norte + 1 )C ( norte+1 )( n>− 1 ) (cuandonnCuando n es un número entero, es n ! sn + 1 \cfrac{n!}{s^{n+1}}snorte + 1n !) |
| porque ω 0 t \cos\omega_0 tporqueVaya0t | π [ δ ( ω + ω 0 ) + δ ( ω − ω 0 ) ] \pi[\delta(\omega+\omega_0)+\delta(\omega-\omega_0)]pag [ re ( o+Vaya0)+d ( o−Vaya0)] | ss 2 + ω 0 2 \cfrac{s}{s^2+\omega_0^2}s2+Vaya02s(requisitosω 0 ∈ R \omega_0\in\mathbb{R}Vaya0∈R) |
| pecado ω 0 t \sin\omega_0 tpecadoVaya0t | yo π [ δ ( ω + ω 0 ) − δ ( ω − ω 0 ) ] i\pi[\delta(\omega+\omega_0)-\delta(\omega-\omega_0)]iπ [ re ( o+Vaya0)−d ( o−Vaya0)] | ω 0 s 2 + ω 0 2 \cfrac{\omega_0}{s^2+\omega_0^2}s2+Vaya02Vaya0(requisitosω 0 ∈ R \omega_0\in\mathbb{R}Vaya0∈R) |
| mi - β tu ( t ) e^{-\beta t}u(t)mi- βt tu(t) | 1 β + yo ω ( β > 0 ) \cfrac{1}{\beta+i\omega}(\beta>0)b+yo1( segundo>0 ) | 1 s + β \cfrac{1}{s+\beta}s+b1 |
3. Propiedades de la transformada de Fourier y la transformada de Laplace
令F ( ω ) = F [ f ( t ) ] F(\omega)=\mathscr{F}[f(t)]F ( ω )=F [ f ( t )],F ( s ) = L [ f ( t ) ] F(s)=\mathscr{L}[f(t)]F ( s )=L [ f ( t )]。
| naturaleza | Transformada de Fourier | Transformada de Laplace |
|---|---|---|
| propiedades lineales | F [ af 1 ( t ) + bf 2 ( t ) ] = a F [ f 1 ( t ) ] + b F [ f 2 ( t ) ] \mathscr{F}[af_1(t)+bf_2(t)] =a\mathscr{F}[f_1(t)]+b\mathscr{F}[f_2(t)]F [ un f1( t )+bf _2( t )]=una F [ f1( t )]+b F [ f2( t )] | L [ af 1 ( t ) + bf 2 ( t ) ] = a L [ f 1 ( t ) ] + b L [ f 2 ( t ) ] \mathscr{L}[af_1(t)+bf_2(t)] =a\mathscr{L}[f_1(t)]+b\mathscr{L}[f_2(t)]L [ una f1( t )+bf _2( t )]=una L [ f1( t )]+b L [ f2( t )] |
| Semejanza | F [ f ( en ) ] = 1 ∣ un ∣ F ( ω un ) \mathscr{F}[f(en)]=\frac{1}{|a|}F\left(\frac{\omega}{ rectamente)F [ f ( un t )]=∣ un ∣1F(aVaya) | L [ f ( at ) ] = 1 a F ( sa ) \mathscr{L}[f(at)]=\frac{1}{a}F\left(\frac{s}{a}\right)L [ f ( un t )]=a1F(as)(a > 0 a > 0a>0) |
| Propiedades simétricas | F [ F ( ω ) ] = 2 π F ( − t ) \mathscr{F}[F(\omega)]=2\pi f(-t)F [ F ( ω )]=2 π F ( - t ) | |
| Propiedades diferenciales | F [ F ′ ( t ) ] = yo ω F [ F ( t ) ] \mathscr{F}[f'(t)]=i\omega\mathscr{F}[f(t)]F [ f′ (t)]=yoω F [ f ( t )] F [ f ( norte ) ( t ) ] = ( yo ω ) norte F [ f ( t ) ] \mathscr{F}[f^{(n)}(t)]={ (i\omega)}^n\mathscr{F}[f(t)]F [ f( n ) (t)]=( yo )norte F[f(t)] |
L [ F ′ ( t ) ] = s F ( s ) − F ( 0 ) \mathscr{L}[f'(t)]=sF(s)-f(0)L [ f′ (t)]=s F ( s )−F ( 0 ) L [ F ( norte ) ( t ) ] = sn F ( s ) − sn − 1 F ( 0 ) − ⋯ − F ( norte − 1 ) ( 0 ) \mathscr{L}[f^{( n)}(t)]=s^n F(s)-s^{n-1}f(0)-\cdots-f^{(n-1)}(0)L [ f( n ) (t)]=snF (s)_−snorte - 1 F(0)−⋯−F( norte - 1 ) (0) |
| 象函数的微分性质 | F [ t f ( t ) ] = i F ′ ( ω ) \mathscr{F}[tf(t)]=iF'(\omega) F[tf(t)]=iF′(ω) F [ t n f ( t ) ] = i n F ( n ) ( ω ) \mathscr{F}[t^n f(t)]=i^n F^{(n)}(\omega) F[tnf(t)]=inF(n)(ω) |
L [ t f ( t ) ] = − F ′ ( s ) \mathscr{L}[tf(t)]=-F'(s) L[tf(t)]=−F′(s) L [ t n f ( t ) ] = ( − 1 ) n F ( n ) ( s ) \mathscr{L}[t^n f(t)]={(-1)}^n F^{(n)}(s) L[tnf(t)]=(−1)nF(n)(s) |
| 位移性质 | F [ f ( t + t 0 ) ] = e i ω t 0 F [ f ( t ) ] \mathscr{F}[f(t+t_0)]=e^{i\omega t_0}\mathscr{F}[f(t)] F[f(t+t0)]=eiωt0F[f(t)] | L [ f ( t + t 0 ) ] = e s t 0 L [ f ( t ) ] \mathscr{L}[f(t+t_0)]=e^{st_0}\mathscr{L}[f(t)] L[f(t+t0)]=est0L[f(t)](要求 t 0 < 0 t_0<0 t0<0) |
| 象函数的位移性质 | F [ e i ω 0 t f ( t ) ] = F ( ω − ω 0 ) \mathscr{F}[e^{i\omega_0 t}f(t)]=F(\omega-\omega_0) F[eiω0tf(t)]=F(ω−ω0) | L [ e a t f ( t ) ] = F ( s − a ) \mathscr{L}[e^{at}f(t)]=F(s-a) L[eatf(t)]=F(s−a)(要求 Re ( s − a ) > s 0 \operatorname{Re}(s-a)>s_0 Re(s−a)>s0,其中 s 0 s_0 s0是 f ( t ) f(t) f(t)的增长指数) |
| 积分性质 | F [ ∫ − ∞ t f ( τ ) d τ ] = 1 i ω F ( ω ) + π F ( 0 ) δ ( ω ) \mathscr{F}\left[\int_{-\infty}^t f(\tau)\mathrm{d}\tau\right]=\frac{1}{i\omega}F(\omega)+\pi F(0)\delta(\omega) F[∫−∞tf(τ)dτ]=iω1F(ω)+πF(0)δ(ω) | L [ ∫ 0 t f ( τ ) d τ ] = 1 s F ( s ) \mathscr{L}[\int_0^t f(\tau)\mathrm{d}\tau]=\frac{1}{s}F(s) L[∫0tf(τ)dτ]=s1F(s) |
| 象函数的积分性质 | L [ f ( t ) t ] = ∫ s ∞ F ( s ) d s \mathscr{L}\left[\frac{f(t)}{t}\right]=\int_s^\infty F(s)\mathrm{d}s L[tf(t)]=∫s∞F(s)ds | |
| 卷积定理 | F [ f 1 ( t ) ∗ f 2 ( t ) ] = F [ f 1 ( t ) ] ⋅ F [ f 2 ( t ) ] \mathscr{F}[f_1(t)*f_2(t)]=\mathscr{F}[f_1(t)]\cdot\mathscr{F}[f_2(t)] F[f1(t)∗f2(t)]=F[f1(t)]⋅F[f2(t)] F [ f 1 ( t ) ⋅ f 2 ( t ) ] = 1 2 π F [ f 1 ( t ) ] ∗ F [ f 2 ( t ) ] \mathscr{F}[f_1(t)\cdot f_2(t)]=\frac{1}{2\pi}\mathscr{F}[f_1(t)]*\mathscr{F}[f_2(t)] F[f1(t)⋅f2(t)]=2π1F[f1(t)]∗F[f2(t)] |
L [ f 1 ( t ) ∗ f 2 ( t ) ] = L [ f 1 ( t ) ] ⋅ L [ f 2 ( t ) ] \mathscr{L}[f_1(t)*f_2(t)]=\mathscr{L}[f_1(t)]\cdot\mathscr{L}[f_2(t)] L[f1(t)∗f2(t)]=L[f1(t)]⋅L[f2(t)] |
| 乘积定理 | 令 F 1 ( ω ) = F [ f 1 ( t ) ] F_1(\omega)=\mathscr{F}[f_1(t)] F1(ω)=F[f1(t)], F 2 ( ω ) = F [ f 2 ( t ) ] F_2(\omega)=\mathscr{F}[f_2(t)] F2(ω)=F[f2(t)],则 ∫ − ∞ + ∞ f 1 ( t ) ‾ f 2 ( t ) d t = 1 2 π ∫ − ∞ + ∞ F 1 ( ω ) ‾ F 2 ( ω ) d ω \int_{-\infty}^{+\infty}\overline{f_1(t)}f_2(t)\mathrm{d}t=\frac{1}{2\pi}\int_{-\infty}^{+\infty}\overline{F_1(\omega)}F_2(\omega)\mathrm{d}\omega ∫−∞+∞f1(t)f2(t)dt=2π1∫−∞+∞F1(ω)F2(ω)dω ∫ − ∞ + ∞ f 1 ( t ) f 2 ( t ) ‾ d t = 1 2 π ∫ − ∞ + ∞ F 1 ( ω ) F 2 ( ω ) ‾ d ω \int_{-\infty}^{+\infty}f_1(t)\overline{f_2(t)}\mathrm{d}t=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F_1(\omega)\overline{F_2(\omega)}\mathrm{d}\omega ∫−∞+∞f1(t)f2(t)dt=2π1∫−∞+∞F1(ω)F2(ω)dω |
|
| 能量积分 | 帕西瓦尔等式: ∫ − ∞ + ∞ [ f ( t ) ] 2 d t = 1 2 π ∫ − ∞ + ∞ ∣ F ( ω ) ∣ 2 d ω \int_{-\infty}^{+\infty}{[f(t)]}^2\mathrm{d}t=\frac{1}{2\pi}\int_{-\infty}^{+\infty}{|F(\omega)|}^2\mathrm{d}\omega ∫−∞+∞[f(t)]2dt=2π1∫−∞+∞∣F(ω)∣2dω |
|
| 初值定理 | f ( 0 ) = lim s → ∞ s F ( s ) f(0)=\lim\limits_{s\to\infty}sF(s) f(0)=s→∞limsF(s)(若这个极限存在) | |
| 终值定理 | lim t → + ∞ f ( t ) = lim s → 0 s F ( s ) \lim\limits_{t\to+\infty}f(t)=\lim\limits_{s\to 0}sF(s) t→+∞limf(t)=s→0limsF(s) (要求 s F ( s ) sF(s) sF(s)的所有奇点都在 s s s平面的左半部) |
四、拉普拉斯逆变换
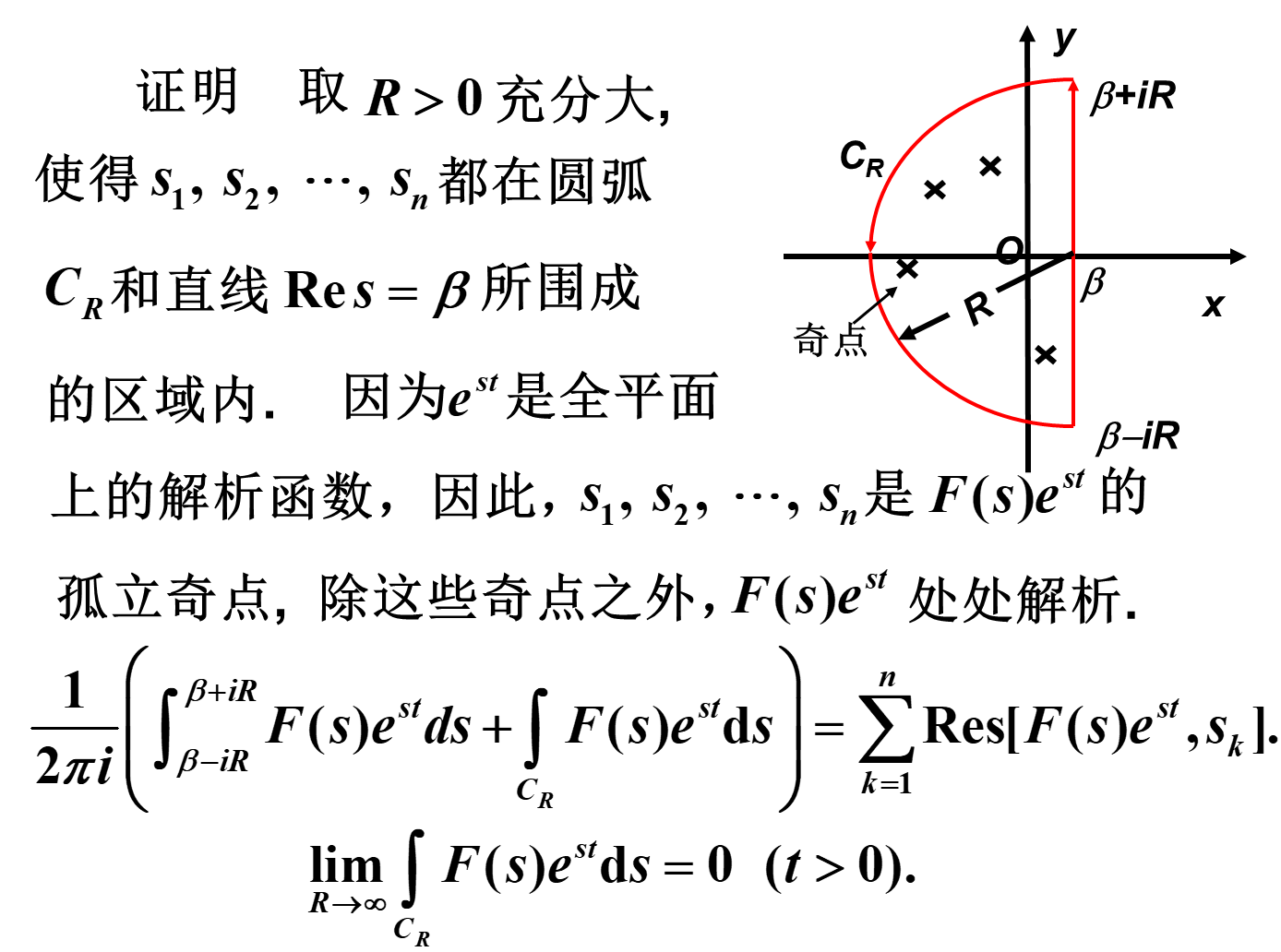
由于 F ( s ) = L [ f ( t ) ] = F [ f ( t ) u ( t ) e − β t ] F(s)=\mathscr{L}[f(t)]=\mathscr{F}[f(t)u(t)e^{-\beta t}] F(s)=L[f(t)]=F[f(t)u(t)e−βt]( s = β + i ω s=\beta+i\omega s=β+iω),我们有 1 2 π ∫ − ∞ + ∞ F ( β + i ω ) e i ω t d ω = f ( t ) u ( t ) e − β t f ( t ) = 1 2 π ∫ − ∞ + ∞ F ( β + i ω ) e ( β + i ω ) t d ω \frac{1}{2\pi}\int_{-\infty}^{+\infty}F(\beta+i\omega)e^{i\omega t}\mathrm{d}\omega=f(t)u(t)e^{-\beta t}\\ f(t)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F(\beta+i\omega)e^{(\beta+i\omega)t}\mathrm{d}\omega 2π1∫−∞+∞F(β+iω)eiωtdω=f(t)u(t)e−βtf(t)=2π1∫−∞+∞F(β+iω)e(β+iω)tdω注意到 d s = i d ω \mathrm{d}s=i\mathrm{d}\omega ds=idω,我们把积分写出复变函数的积分: f ( t ) = 1 2 π i ∫ β − i ∞ β + i ∞ F ( s ) e s t d s f(t)=\frac{1}{2\pi i}\int_{\beta-i\infty}^{\beta+i\infty}F(s)e^{st}\mathrm{d}s f(t)=2πi1∫β−i∞β+i∞F(s)estds下面我们通过留数来计算这个积分。
定理 设 s 1 , s 2 , ⋯ , s l s_1,s_2,\cdots,s_l s1,s2,⋯,sl是 F ( s ) F(s) F(s)的所有孤立奇点(有限个),除这些点外, F ( s ) F(s) F(s)处处解析。且存在 R 0 > 0 R_0>0 R0>0,使得当 ∣ s ∣ > R 0 |s|>R_0 ∣s∣>R0时, ∣ F ( s ) ∣ ≤ M ( r ) |F(s)|\le M(r) ∣F(s)∣≤M(r),其中 M ( r ) M(r) M(r)是 r r r的实函数,满足 lim r → + ∞ M ( r ) = 0 \lim\limits_{r\to+\infty}M(r)=0 r→+∞limM(r)=0(即当 s → ∞ s\to\infty s→∞时, F ( s ) → 0 F(s)\to 0 F(s)→0)。选取 β \beta β,使所有孤立奇点的实部都小于 β \beta β,则当 t > 0 t>0 t>0时, f ( t ) = 1 2 π i ∫ β − i ∞ β + i ∞ F ( s ) e s t d s = ∑ k = 1 l Res [ F ( s ) e s t , s k ] f(t)=\frac{1}{2\pi i}\int_{\beta-i\infty}^{\beta+i\infty}F(s)e^{st}\mathrm{d}s=\sum\limits_{k=1}^l \operatorname{Res}[F(s)e^{st},s_k] f(t)=2πi1∫β−i∞β+i∞F(s)estds=k=1∑lRes[F(s)est,sk]