Las redes neuronales gráficas (GNN) representan una clase poderosa de arquitecturas de redes neuronales profundas. En un mundo cada vez más interconectado, la mayor parte de la información se puede modelar como un gráfico debido a su conectividad. Por ejemplo, los átomos de un compuesto son nodos y los enlaces entre ellos son aristas.
La belleza de las redes neuronales de gráficos es su capacidad para operar directamente con datos estructurados en gráficos sin sacrificar detalles importantes. Esto es especialmente evidente cuando se trata de conjuntos de datos complejos, como compuestos químicos, donde los GNN nos permiten aprovechar al máximo la riqueza de la representación gráfica subyacente. Al hacerlo, los GNN pueden obtener una comprensión más completa de las relaciones entre átomos y enlaces, abriendo vías para análisis más precisos y profundos.
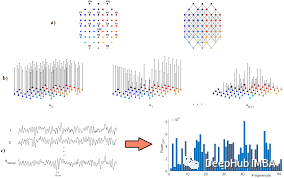
Fuera de la química, la influencia de las estructuras gráficas se extiende a diferentes campos. Tomemos como ejemplo los datos de transporte, donde las ciudades son nodos y las rutas entre ellas son bordes. Los GNN han demostrado ser invaluables en tareas como la predicción de atascos de tráfico, lo que demuestra su eficacia para capturar la compleja dinámica de la movilidad urbana. La capacidad de las GNN para captar las dependencias espaciales y los patrones inherentes a los datos gráficos se convierte en una herramienta poderosa cuando se enfrentan desafíos como la predicción de la congestión del tráfico. Numerosos modelos basados en GNN se han convertido en las soluciones más avanzadas para predecir la congestión del tráfico, convirtiéndose en los modelos más punteros. El siguiente es un modelo para predecir atascos de tráfico en documentos con código, básicamente todos GNN.
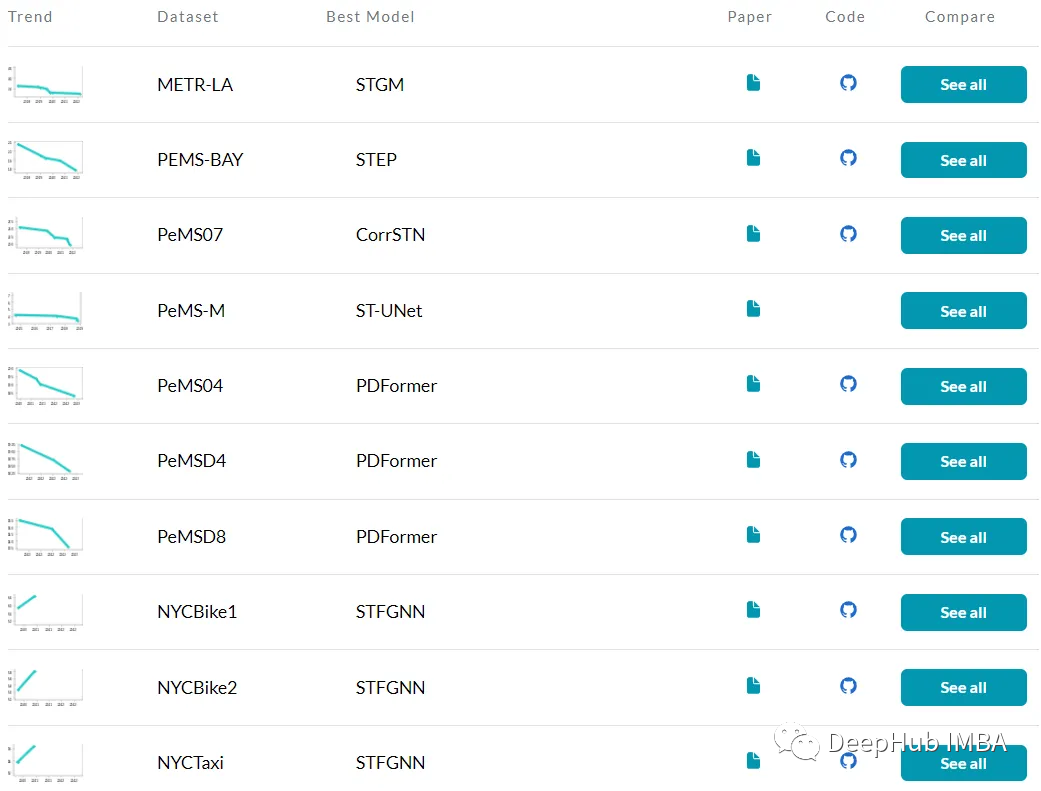
Este artículo presentará la base teórica de la convolución de gráficos. Al profundizar en la complejidad de la transformada de Fourier del gráfico y su conexión con las convoluciones del gráfico, sentaremos las bases para una comprensión profunda de este concepto clave en el mundo GNN.
Cómo definir la convolución del gráfico
El concepto central de GNN es la convolución de gráficos, que realiza un procesamiento efectivo de datos de gráficos al capturar la relación entre nodos y bordes.
Entre los diversos métodos para comprender la convolución de gráficos, este artículo se centra en utilizar la teoría de la transformada de Fourier de gráficos para explicar. Este concepto proporciona una visión única del mecanismo de convolución de gráficos.
La transformada gráfica de Fourier nos permite representar señales gráficas (datos asociados con nodos) en términos de frecuencias gráficas. Esta descomposición, basada en el análisis espectral, proporciona información sobre los patrones y estructuras subyacentes en el gráfico.
Algunas arquitecturas GNN utilizan mecanismos de atención y otros métodos avanzados que van más allá del alcance de las convoluciones de gráficos. Pero discutimos principalmente la naturaleza de la convolución del gráfico y su interacción con la transformada de Fourier del gráfico, por lo que la atención y otras partes están fuera del alcance de este artículo.
¿Qué es la transformada del gráfico de Fourier?
El concepto de transformada de Fourier de un gráfico tiene similitudes interesantes con la transformada de Fourier clásica. Así como la transformada de Fourier tradicional descompone una señal de onda en sus frecuencias constituyentes, la transformada gráfica de Fourier opera con datos estructurados en gráficos, revelando las frecuencias de la señal incrustadas en ellos.
Imagine un gráfico ponderado no dirigido sin ciclos ni estructuras de bordes múltiples. La transformada de Fourier de un gráfico es una operación matemática que enfatiza la transformación de la señal presente en el gráfico. Este concepto resulta particularmente ilustrativo en el caso de dimensiones de señal iguales a uno. Considere la siguiente descripción, que muestra cómo se ve una señal en un gráfico [1].
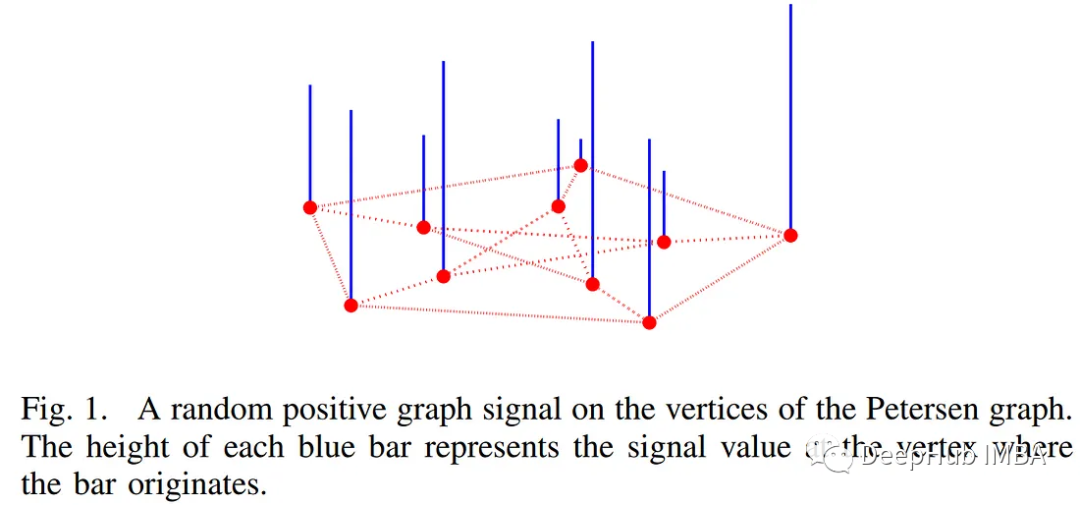
Descomponer una señal en su gráfico de frecuencia, o transformada gráfica de Fourier, proporciona una manera de identificar las diversas relaciones, regularidades y complejidades inherentes a los datos del gráfico.
Gráfico laplaciano
Para comprender la transformada de Fourier de un gráfico, comenzaremos con una exploración básica, presentando primero la transformada de Laplace de un gráfico. Este concepto clave es la piedra angular para revelar las propiedades de frecuencia intrínsecas de los gráficos.
El gráfico laplaciano se denota como L y se define como:
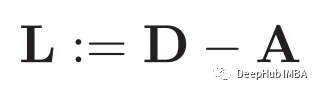
En esta ecuación, A denota la matriz de adyacencia, que codifica las conexiones entre los nodos en el gráfico, y D denota la matriz de grados, que captura el grado de cada nodo.
Dado que D y A son matrices simétricas reales, la matriz laplaciana gráfica también tiene las propiedades de las matrices simétricas reales. Esta propiedad nos permite realizar una descomposición espectral de la función laplaciana gráfica, expresada como:
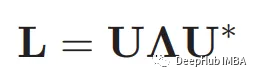
En la fórmula anterior, U representa la matriz de vector propio y Λ es una matriz diagonal compuesta de valores propios (Λ 1, Λ 2, ..., Λ n).
Cuadrático
Esta sección explica la forma cuadrática y la forma cuadrática de un gráfico laplaciano y cómo se relaciona con la frecuencia de la señal del gráfico.
La forma cuadrática de un gráfico laplaciano se puede definir como:
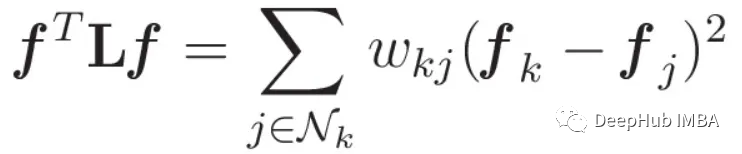
Aquí f representa la señal del gráfico, w representa el peso de un borde y Nk representa el conjunto de nodos conectados al nodo k.
Esta representación revela dos aspectos clave fundamentales:
suavidad de la función
Las formas cuadráticas brindan información sobre la fluidez gráfica de las funciones. Considere el escenario donde f = [1,1,1,...,1]T. Según la definición del gráfico laplaciano, la forma cuadrática se evalúa como cero. Es decir, cuanto más suave sea la función entre los nodos, más pequeña será la forma cuadrática resultante. Esta interacción proporciona un mecanismo para cuantificar el grado de suavidad inherente de las señales gráficas.
Similitud entre nodos vecinos
La forma cuadrática también se utiliza como métrica para evaluar la similitud entre señales en nodos vecinos. Cuando la diferencia entre f(i) y f(j) es grande, el valor cuadrático correspondiente aumenta proporcionalmente. Por el contrario, si las señales en nodos adyacentes son similares, la forma cuadrática tiende a cero. Esta observación es consistente con la idea de que valores más grandes de forma cuadrática reflejan una mayor variación entre nodos adyacentes.
Con estos conceptos en su lugar, las formas cuadráticas pueden interpretarse como un sustituto gráfico de la "frecuencia" de la función. Al usarlo para proporcionar información, podemos realizar una descomposición gráfica de la señal basada en componentes de frecuencia. Este paso crucial es el precursor de la transformada gráfica de Fourier, y abre una forma poderosa de revelar características de frecuencia integradas en datos estructurados gráficamente.
Transformada gráfica de Fourier
Hemos establecido la forma cuadrática del gráfico laplaciano como un indicador de la frecuencia de la señal, donde los valores de forma cuadrática más grandes indican frecuencias más altas. Un punto más importante: tenga en cuenta que estos valores pueden verse afectados por la norma de f. Para garantizar la coherencia y eliminar los efectos potenciales de diferentes normas, también debemos imponer la restricción de que la norma de f sea igual a 1.
Para obtener el valor estacionario de la forma cuadrática bajo la condición de norma, utilizamos el método del multiplicador de Lagrange, una poderosa técnica de optimización. Transformando adecuadamente el problema, finalmente obtenemos un problema de valores propios:
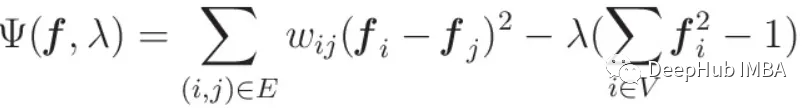
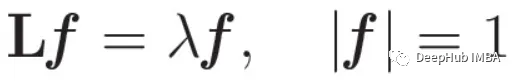
Este valor propio proporciona una relación: cada valor propio de L refleja el valor de la forma cuadrática del gráfico laplaciano. En pocas palabras, estos valores propios capturan las frecuencias a las que vibra la señal gráfica.
Esto nos da una comprensión básica de los valores propios como indicadores de la frecuencia de una función. La conexión entre los vectores propios y el gráfico laplaciano se convierte en la forma de realizar la transformada de Fourier del gráfico, un proceso que revela sistemáticamente los elementos de frecuencia intrínsecos de la señal del gráfico.
Ahora, podemos ver la definición de la transformada de Fourier.
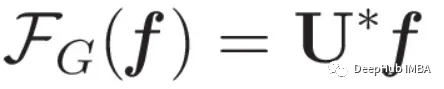
De la transformada de Fourier del gráfico a la convolución del gráfico
Con la transformada gráfica de Fourier presentada anteriormente, obtenemos una poderosa herramienta para analizar y procesar señales gráficas de manera eficiente. En nuestro estudio, la conexión entre la transformada de Fourier del gráfico y la convolución del gráfico.
En el centro de esta conexión se encuentra el teorema de convolución, que establece la conexión entre la operación de convolución y el producto de elementos en el dominio de Fourier.
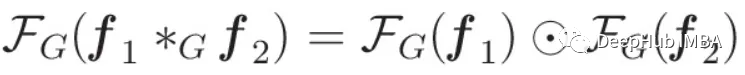
La operación de convolución es similar a la multiplicación por elementos de la señal transformada en el dominio de Fourier. Se puede derivar una definición indirecta de convolución de gráficos utilizando el teorema de convolución:
- Realiza una transformada de Fourier en una señal gráfica.
- Multiplique la señal transformada con un vector de peso que se pueda aprender.
- Realice una transformada de Fourier inversa en el producto de elementos para obtener el resultado de la convolución del gráfico.
La fórmula para la convolución del gráfico ahora se puede expresar de la siguiente manera:
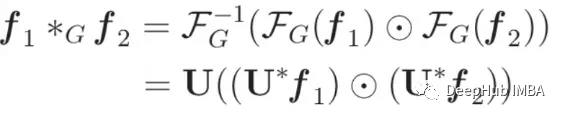
Para simplificar esta definición, introducimos una parametrización de utilidad. Dado que el producto del elemento con U f se puede expresar como el producto con diag(U f), s, el peso aprendible θ se establece como:

Al explotar esta parametrización, la formulación de convolución del gráfico de gθ adopta una forma simplificada e intuitiva:
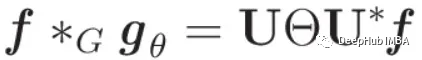
¡Mira, hemos definido una convolución de gráfico a partir de la transformada de Fourier de un gráfico!
Resumir
En este artículo, comenzamos revelando los principios básicos del gráfico laplaciano y luego profundizamos en el concepto básico de convolución del gráfico, que es la derivación de la transformada de Fourier del gráfico.
Las inferencias realizadas en este artículo deberían profundizar su comprensión de la naturaleza de la convolución de gráficos. Presentaremos el mecanismo de transmisión de mensajes del gráfico con más detalle más adelante, porque puede agregar información de nodos adyacentes, que es la clave para el éxito de la convolución del gráfico.
Cita:
[1] DI Shuman et al., “El campo emergente del procesamiento de señales en gráficos: extensión del análisis de datos de alta dimensión a redes y otros dominios irregulares”, Revista IEEE Signal Processing, 30(3):83–98, 2013
https://avoid.overfit.cn/post/dbcee95a7b8444e8b5f0e0925ec66332
Autor: Lalf