定性分析
这个方程的整数解怎么得到?参考视频
方程:
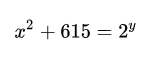
函数f1、f2和f3:
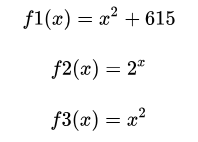
f1和f2的导数,也就是曲线f的斜率, 理论上f2的斜率是比f1越来越陡峭,f1和f2只有有限的几个交点。
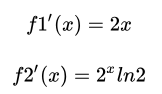
方程的整数解是曲线f1和f2的交点。 由于f1画图不方便, 可以从f2和f3的形态推知f1和f2只有有限的交点。因为f3只是f1的平移。 f2和f3的图像示意如下, 明显只有有限个交点。
大力出奇迹
思路
不管三七二十一,x和y都从0开始,按照自然数递增的方式去试探。
两层循环,外层是x, 内层是y。然后尝试计算f1和f2, 如果f1 == f2 就打印结果,终止循环。
不过这里可做一点点局部优化,就是x^2+615=2^y >=615 可以推出y>9。外层循环x 从0开始,内存循环可以从10开始。
代码
equation.cpp
#include <iostream>
#include <cmath> using namespace std; int main(int argc, char* argv[]) { if (argc < 3) return -1; long n = atol(argv[1]); long m = atol(argv[2]); bool flag = false; //找到解的标志,找到为true未找到为false for (long x = 0; x < n && !flag; x++) //x没到循环上限值且未找到解的就继续 { for (long y = 10 ; y < m; y++) { long long f1 = 615 + pow(x, 2); long long f2 = pow(2, y); if (f1 == f2) //找到,打印解 { flag = true; cout << "(x, y)" << ":" << "(" << x << "," << y << ")" << endl; cout << "(x, y)" << ":" << "(" << -x << "," << y << ")" << endl;//共轭解 break; } } } return 0; } 复制代码代码解读
n 和 m是通过命令输入,来控制x和y的上限的。
flag 为找到解的标志。
外层循环的终止条件是表示式 x < n && !flag 的值为false。
这个解法非常自然,基本属于大力出奇迹的范围。
执行结果
局部优化
思路
- 减少外层循环次数。
- 参考视频,推断x的形式为6k+1或6k-1 ,k为整数
代码
#include <iostream>
#include <cmath> using namespace std; int main(int argc, char* argv[]) { if (argc < 3) return -1; long n = atol(argv[1]); long m = atol(argv[2]); bool flag = false; for (long k = 1; k < n && !flag; k++) { for (long y = 10 ; y < m; y++) { long long f1 = 615 + pow(6*k - 1, 2); long long f2 = pow(2, y); if (f1 == f2) { flag = true; cout << "(x, y)" << ":" << "(" << 6*k - 1 << "," << y << ")" << endl; cout << "(x, y)" << ":" << "(" << -(6*k -1) << "," << y << ")" << endl; break; } f2 = 615 + pow(6*k + 1, 2); if (f1 == f2) { flag = false; cout << "(x, y)" << ":" << "(" << 6*k + 1 << "," << y << ")" << endl; cout << "(x, y)" << ":" << "(" << -(6*k + 1) << "," << y << ")" << endl; break; } } } return 0; } 复制代码代码解读
n 和 m是通过命令输入,来控制x和y的上限的。
flag 为找到解的标志。
外层循环的终止条件是表示式 k < n && !flag 的值为false。
这个解法跟大力出奇迹思路一样,只是先做了一点简单的推断,判定出x的形式,相比方法一,可以少67%的循环次数。
执行结果
全局优化
思路
- 去掉一层循环。 我们可以先计算2^y 的结果,根据方程去推出算出x的值: x = sqrt(2^y - 615)。 x取整后,在根据取整的结果去计算 [x]^2 + 615是否跟2^y值相等。这里[x]表示对x取整。
- 去掉pow调用,只改用一次sqrt。计算2^y的时候, 可以根据外层循环的次数来累乘2得出。
- y肯定大于9, 不必做无谓的计算,所以从10开始。
代码
#include <iostream>
#include <cmath> using namespace std; int main(int argc, char* argv[]) { if (argc < 2) return -1; long n = atol(argv[1]); long long p = 512; //2^9 == 512 for (long y = 10; y < n; y++) { p *= 2; long x = sqrt(p - 615); if (x *x + 615 == p) //判断x确实是整数且满足方程 { cout << "(x, y) = " << "(" << x << "," << y << ")" << endl; cout << "(x, y) = " << "(" << -x << "," << y << ")" << endl; } break; } return 0; } ### 代码解读 p 存储2^y 值,倒推x值, 取整后计算x^2 + 615,是否跟2^y相等。 本方法也不需要flag这种标志了,因为只有一层循环,直接break即可终止。 ### 执行结果 复制代码代码解读
减少一层循环,在循环内只有一次sqrt调用。理论上,应该比方法一和方法二都要高效。
执行结果
总结
三个方法中,显然方法三是比较优的方法。
本案例提升效率的方法:
-
局部优化,譬如从数学角度先做优化
-
全局优化,不但要从数学角度,而且逆向思维,从y出发导出x,再从x去验算y。
-
避免都充循环
-
在循环中尽量少用函数调用,可以多采用简答的加法和乘法。
必果学院
腾讯课堂必果学院是一个致力于C/C++/Python全栈学习的平台。必果学院提供从MFC/QT的客户端到linux服务器,嵌入式到物联网,游戏开发到游戏破解等一站式教学。适合0基础的对编程感兴趣初高中学生及以程序员为目标职业的在校大学生和初入职场不就亟待提升的初中级程序员。
加群获取资料
-
C/C++ QT/UI
-
Linux 高级开发
-
区块链
-
软件工程