数据结构部分2

2章
a接口与实现
1.说法正确的是：同一个抽象数据类型可能用多种数据结构实现。
2.在一个初始为空的向量上依次执行：insert(0, 2), insert(1, 6), put(0, 1), remove(1), insert(0, 7) 后的结果是：{7, 1}
3.以下代码是向量复制代码的一个变体且语义与其相同，空格处应填入的内容为：
–hi
解析:该代码是从后向前复制。根据视频中代码的语义，复制的范围是A[lo, hi)。
b.可扩充接口
1.在一个初始最大容量为10的空向量上依次执行：insert(0, 2), insert(1, 6), put(0, 1), remove(1), insert(0, 7) 后的装填因子是：20%
解析:经过这些操作后的向量为{7, 1}。装填因子=实际所用容量/最大容量。
2.是否可以将视频里向量扩容代码中的：

for (int i = 0; i < _size; i++) _elem[i] = oldElem[i];

in the vector expansion code in the video with: 替代为：

memcpy(_elem, oldElem, _size * sizeof(T));
答：不能，因为后者能否达到目的与元素类型T有关。
解析：当T为非基本类型且有对应的赋值运算符以执行深复制时，前一段代码会调用赋值运算符，而后一段只能进行浅复制。
3.采用每次追加固定内存空间的扩容策略，规模为n的向量插入元素的分摊时间复杂度为：
$\Theta(n)$

4.分别采用每次追加固定内存空间和每次内存空间翻倍两种扩容策略，规模为n的向量插入元素的分摊时间复杂度分别为：
$\Theta(n),\Theta(1)$

5.关于平均复杂度和分摊复杂度，说法错误的是：分摊复杂度得到的结果比平均复杂度低
解析:分摊复杂度和平均复杂度的结果并没有必然联系

c.无序向量
1.T & Vector::operator[](Rank r) { return _elem[r]; } 中的返回值T&是什么意义？
答：这是类型T的引用，使用它是因为返回值可以作为左值
解析： V[0] = 1 左值即位于赋值号“=”左边的值。只有返回值可以作为左值，才能通过以下表达式修改向量：V[0] = 1
2.如果insert（）函数中的FOR循环更改为以下形式会发生什么？
答：会覆盖原向量中秩大于r的所有元素
解析：执行该代码后，原向量中秩为r的元素覆盖了后面的所有元素。
3. 为什么区间删除算法remove(lo, hi)中要从前向后移动被删除元素的后缀？
答：因为可能会覆盖部分元素
解析：不妨考虑在{1,2,3}中删除秩为0的元素
4.对于deduplicate()算法，向量规模为n时的最坏时间复杂度为：
$\Theta({n}^{2})$
解析：外循环迭代 $\Theta(n)$次，每次内循环需要 $\Theta(n)$的时间
5.作为一个函数对象的类XXX，它必须显式定义以下哪个成员函数：
operator()()
解析：对于函数对象来说，()是用于执行函数调用的操作符

d1.有序向量-唯一化
1.disordered()算法的返回值是：相邻逆序对个数
解析：相邻逆序对即两个相邻的元素{…i, j…}且i>j。而逆序数是逆序对的个数，并不要求二者相邻。
4. 有序向量中的重复元素：必定全部紧邻分布
3.对于规模为n的向量，低效版uniquify()的最坏时间复杂度为： $\Theta(n^2)$
解析：每次删除元素都要移动被删除元素的所有后继
5. 为什么该算法中不需要调用remove()进行元素删除？
重复元素被直接忽略了
解析：有序向量中重复元素必然紧邻，而算法中忽略了互异元素间的重复元素
5.对于规模为n的向量，高效版uniquify()的最坏时间复杂度为： $\Theta(n)$
解析：重复元素被直接忽略了

d2.有序向量-二分查找
1.对于规模为n的向量，查找失败时find()的返回值是：-1
2.在有序向量V中插入元素e并使之保持有序，下列代码正确的是:V.insert(V.search(e) + 1, e);
3.在binsearch(e, lo, hi)版本A中，若V[mi] < e，则下一步的查找范围是：
V(mi, hi]
解析：此时e在V[mi]右侧
4.Rank mi = (lo + hi) >> 1 等效于下列哪个表达式?（lo和hi非负）
解析：Rank mi = (lo + hi) / 2
5. V={2, 3, 5, 7, 11, 13, 17}。V.search(16, 0, 7)需要进行多少次比较？5
解析：画个图就知道了
6.V1={2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61}

V2={1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18}
在V1中查找43的查找长度是x，则在V2中查找14的查找长度为：x

d3.有序向量-斐波那契
1.fibSearch()算法与binSearch()有什么区别？二者选取轴点mi的方式不同
解析：二分查找一般选取中点为mi，而Fibonacci查找利用Fibonacci数列选取一个从位置上来看非平衡的mi
2.:V={1, 2, 3, 4, 5, 6, 7}，在V中用Fibonacci查找元素1，被选取为轴点mi的元素依次是：5,3,2,1
3.为什么说binSearch()版本A的查找过程并不平衡?
因为向左、向右两个分支所需要的比较次数不相等
解析: 每次向左经过了1次比较，向右则经过了2次比较

d4.改进的二分查找
1.对于规模为n的向量，二分查找版本A和B的最优时间复杂度分别为：
$\Theta(1),\Theta(log_2n)$
解析：版本A的最优情况即第一次就命中，只需Θ(1)的时间
2.对于search()接口，我们约定当向量中存在多个目标元素时返回其中：
秩最大者
3.对于二分查找版本C，当e<V[mi]不成立时下一步的查找范围是：
V(mi, hi)
4.对于二分查找版本C，当查找区间的长度缩小为0时，V[lo]是：
$ min{0\leq r < n|e < V[r]} $
解析：参见版本C正确性证明中的不变性。注意lo - 1才是我们需要的返回值

d5.插值查找
1.如果（有序）向量中元素的分布满足独立均匀分布（排序前），插值查找的平均时间复杂度为：O(loglogn)
2.在向量V={2, 3, 5, 7, 11, 13, 17, 19, 23}中用插值查找搜索元素7,猜测的轴点mi=1

e.起泡排序
1.对V进行两次扫描交换后V[6] =17
解析：每次扫描交换后原无序部分的最大元素必然就位，故所求答案为整个向量中的次大元素
2.经改进的起泡排序在什么情况下会提前结束？
完成的扫描交换趟数 = 实际发生元素交换的扫描交换趟数 + 1
解析：另一个说法是：某趟扫描交换中没有发生元素交换
3.试用以下算法对V={19, 17, 23}排序：
(1) 先按个位排序
(2)在上一步基础上，再按十位排序
这个算法的是否正确？若第2步用的排序算法是稳定的，则正确
解析：若第2步不稳定，可能的情况是：{19, 17, 23} -> {23, 17, 19} -> {19, 17, 23}
以上算法称为“基数排序（radix sort）“，适用于被排序元素可分为若干个域的情况，它的正确性要依赖于对每个域分别排序时的稳定性

f.归并排序
1.归并排序时间复杂度的递推公式 $T(n)=2T(\frac{n}{2})+O(n)$的解是什么？其中 $O(n)$项代表什么？
$O(nlog_2n)$,归并两个已排序子向量的时间
解析：对两个子向量分别排序的时间是 $2T(\frac{n}{2})$
2.对{2, 5, 7}和{3, 11, 13}进行二路归并，执行的元素比较依次是：
2与3、5与3、5与11、7与11
解析：每次比较两个子向量中的最小元素并取出其中更小者
3.对于规模为n的向量，归并排序的最优、最坏时间复杂度分别为：
$\Theta(nlog_2n),\Theta(nlog_2n)$
解析： $T(n)=2T(\frac{n}{2})+\Theta(n)$

向量测试
1.分别采用每次追加固定内存空间和每次内存空间翻倍两种扩容策略，在规模为n的向量中插入一个元素的分摊时间复杂度为：
$O(n),O(1)$
2.在有序向量V中插入元素e并使之保持有序，代码正确的是:
V.insert(V.search(e) + 1, e);
解析：search(e)的返回值是不大于e的元素的秩的最大者
3.二分查找“版本C”摘录如下：
向量V={2, 3, 5, 7, 11, 13, 17, 19}，在V中使用它查找目标元素16，整个过程中与目标元素发生过比较的元素依次为：
11, 17, 13

4.二分查找“版本C”摘录如下：
当数组A中有多个待查找元素e时，函数的返回值为：

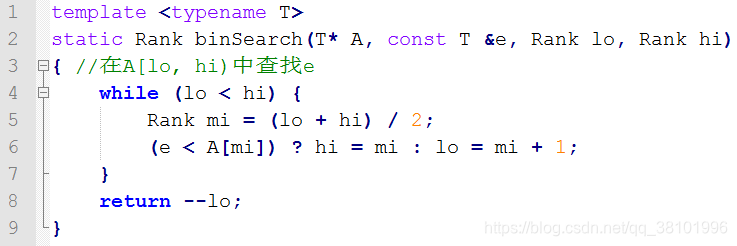
返回秩最大者
解析：注意程序中的“ ? : ”表达式，根据它可以证明本程序有如下循环不变量：任意时刻A[hi, n-1]中元素均>e。而循环结束时有lo==hi，所以返回的元素的直接后继>e，故返回的是秩最大者。也可以直观的理解为由于lo = mi + 1，当有多个元素e时程序总是倾向于命中右边的。

5.:以下函数是二分查找的递归版：
对于规模为n的向量，该递归版的时间、空间复杂度和课堂上所学的迭代版的时间、空间复杂度分别是：

$O(log_2(n)), O(log_2(n)),O(log_2(n)),O(1)$
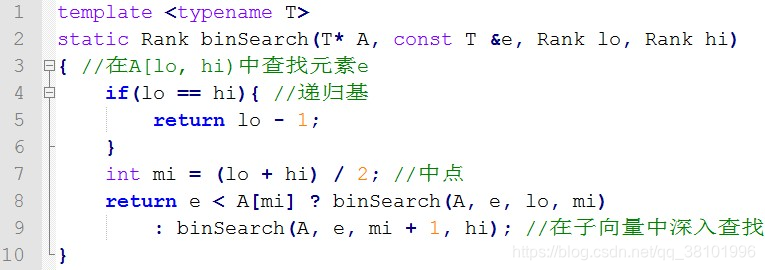
解析： 该递归版与迭代版执行流程相似，时间复杂度相同，但是递归版的空间复杂度等于最大递归深度，在此处即Θ(〖log〗_2 n)，而迭代版只用了常数单位的辅助空间。

6. 向量V={1, 2, 3, 4, 5, 6, 7}，在V中用斐波那契查找查找目标元素1，被选取为轴点mi的元素依次是：
   5, 3, 2, 1
   7.对{2, 5, 7}和{3, 11, 13}进行二路归并，执行的元素比较依次是：
   2与3、5与3、5与11、7与11
   解析：每次比较两个子向量中的最小元素并取出其中更小者

8.在起泡排序的任何一趟扫描交换过程中，若最后一次交换是将元素X > Y交换为Y < X，则此后：
X未必就位，而Y必然
解析:这正是借助last标志，改进bubblesort()的原理和依据

9.在一个初始为空的向量上依次执行：insert(0, 2), insert(1, 6), put(0, 1), remove(1), insert(0, 7) 后的结果是：
{7, 1}

10.以下代码通过不断删除单个元素实现向量的区间删除：其中重载函数remove(Rank r)完成删除单个元素的操作，其时间复杂度正比于被删除元素的后继个数。 对于规模为n的向量，该区间删除算法的最坏时间复杂度为：

$O(n^2)$
解析： 最坏情况是删除整个向量，每删除一个元素，它的后继都需要被移动，故总的时间复杂度为(n-1)+(n-2)+…+1=O(n^2)