SVM详细推导（包含dual-form的推导过程）

线性可分

SVM关于二分类问题的算法，也就是将一组数据线性的分成两类，什么是线性的分成两类呢？就是像图（1）这样的数据用一条线可以进行一分为二。

像图（2）这种数据使用一条线是分不开的，那么这种数据就成为线性不可分的数据，对于这种数据SVM就没有办法了吗？当然有办法了不然也不会在早期这么流行的。

SVM

margin的概念

假设现在有这样一组数据， $D=\{(x_1,y_1),(x_2,y_2),(x_3,y_3)...(x_n,y_n)\}，$其中 $x$表示数据， $y$表示对应的标签， $y\in\{1,-1\}$现在用图（3）来表示：

现在用一条线来区分，假设这条线为： $W^Tx_i+b$来表示，也就是说 $W^Tx_i+b\geq0$时 $，y=1，$ $W^Tx_i+b\leq0$时 $，y=-1$也可以用 $(W^Tx_i+b)\cdot y\geq0$来表示。

图（4）表示的是我们使用了 ①，②和③条作为决策边界来进行将数据分类，从图中我们明显看到这三条线都成功的将数据进行了分类，但是那个分类的最好呢，答案是②，①和③距离数据太近了，有可能造成误判，并且很容易过拟合，对于②来说我们离数据的距离比较远，增加一些噪音的话也是可以保证分类的正确性。

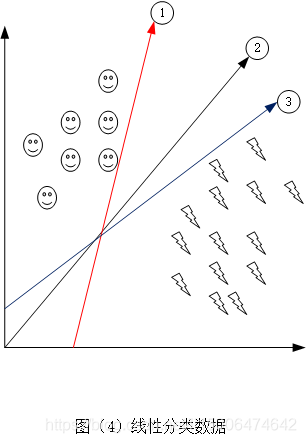
因此我们通常把这个距离叫做margin。我们的分类器离数据的距离越大越好，所以margin的目标就是最大化margin。

margin的计算

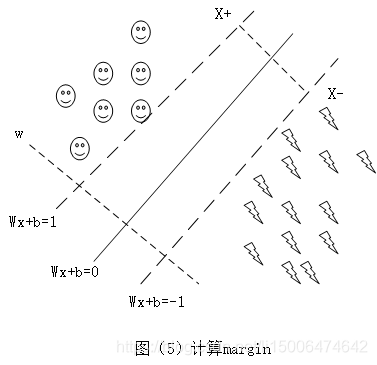
那么margin该怎么计算呢？由图（5）我们可以看到 $Wx+b=0$表示决策边界另外我们设置两条线 $W^Tx+b=1$和 $W^Tx+b=-1$表示分别表示数据集中最外围，所以margin就是这两条线之间的距离，这里因为有 $W和b$的存在，所以我们将其设置为1和-1

假设 $x_+$表示 $W^Tx+b=1$上的点， $x_-$表示 $W^Tx+b=-1$上的点， $margin=|x_+-x_-|$, $w$表示与这三条线垂直的方向

我们可以得到三个公式：
$\begin{cases}W^Tx_++b=1 \quad①\\ W^Tx_-+b=-1\quad②\\ x_+=x_-+\lambda w \quad③\end{cases}$

现在我们来计算 $margin$将③式代入①中得：
$W^T(x_-+\lambda w)+b=1$

$W^Tx_-+W^T\lambda w+b=1\quad ④$
将④-②得
$\lambda W^T w=2$

$\lambda =\dfrac{2}{W^T w}$

$margin=|x_+-x_-|$由③可知： $margin=|\lambda w|=|\dfrac{2}{W^T w} \cdot w|=|\dfrac{2}{W^T }|$

所以最后
$margin=|\dfrac{2}{W^T }|$

SVM的目标函数

svm的目标就是最大化 $margin$也就是：
$maxmize \dfrac{2}{||W^T||}$

$st:\quad W^Tx+b \geq1\quad if:y=1$

$\quad \quad W^Tx+b \leq-1\quad if:y=-1$

我们来简单改变一下公式：

$minemize||W^T||^2$

$st:\quad W^Tx+b \geq1\quad if:y=1$

$\quad \quad W^Tx+b \leq-1\quad if:y=-1$

把条件整合一下

$minemize||W^T||^2$

$st:\quad (W^Tx+b )\cdot y\geq1$

这个就是SVM的目标函数

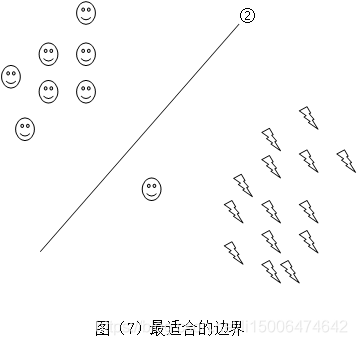
但是现在有一个问题：现实情况下往往会出现如图（6）

这种情况按照我们的算法最后计算出来的边界是①，但是我们可以看出其实 ①并不是最适合的，往往图（7）中的②才是最适合的

也就是说在svm算法中我们允许一些误差的存在，如图（8）

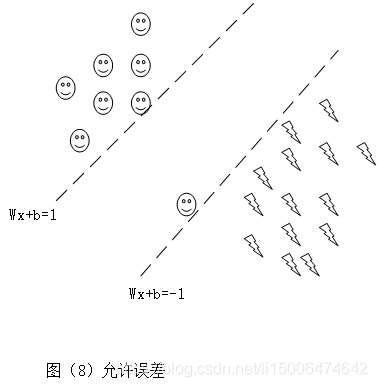
在margin范围内存在一些误差：

所以我们软化SVM的目标函数：

软化SVM的目标函数

$minemize||W^T||^2$

$st:\quad (W^Tx_i+b )\cdot y_i\geq1-\varepsilon_i$

$\quad \quad\varepsilon_i\geq0$

$\varepsilon_i$表示误差的程度

虽然我们允许有误差，但是我们也不能让误差太多了，所以我们在公式中增加了 $\varepsilon$正则项:

$minemize||W^T||^2+\lambda\sum_{i=1}^n \varepsilon_i$

$st:\quad (W^Tx_i+b )\cdot y_i\geq1-\varepsilon_i$

$\quad \quad\varepsilon_i\geq0$

当然了我们希望误差越小越好所以根据：

$(W^Tx_i+b )\cdot y_i\geq1-\varepsilon_i$

我们可以得出：

$\varepsilon_i\geq1-(W^Tx_i+b )\cdot y_i$

也就是说： $\varepsilon_i$最小为 $1-(W^Tx_i+b )\cdot y_i$所以我们确保: $\varepsilon_i=1-(W^Tx_i+b )\cdot y_i$也就保证了误差最小，那么我们把这种信息放到公式里：

$minemize||W^T||^2+\lambda\sum_{i=1}^n max[0,1-(W^Tx_i+b )\cdot y_i]$

如果 $\varepsilon_i$小于0的时候为0，大于0的时候为 $1-(W^Tx_i+b )\cdot y_i$

这里的 $\lambda$也就是超参数，如果 $\lambda$特别大的话，那么我们要求的误差就越小。
$max[0,1-(W^Tx_i+b )\cdot y_i]$也就是比较有名的hinge-loss

梯度下降优化参数

这样我们做梯度下降的时候就得判断一下

梯度下降法：

$w,b$的初始化

循环：1…n:
$\quad \quad if\quad1-(W^Tx_i+b )\leq0:$
$\quad \quad\quad \quad W=W-\eta2W$
$\quad \quad else:$
$\quad \quad\quad \quad W=W-\eta(2W+\lambda\dfrac{\partial(1-(W^Tx_i+b ))}{\partial W})$

$\quad \quad\quad \quad b=b-\eta(\lambda\dfrac{\partial(1-(W^Tx_i+b ))}{\partial b})$

你以为就这样完啦？No NO nO 现在这种算法只能计算线性可分的数据，我在开头说了，它也可以计算非线性的数据，下面计算一下SVM的由primal-form到dual-form

SVM的由primal-form到dual-form

primal-form指的是用正常的逻辑思维进行构建的目标函数，那么为什么转换到dual-form（对偶的问题）一般情况下有两种原因：

1、primal-form的问题比较难以解决因此转换到dual-form

2、在dual-form中可以看到一些有趣的现象

在SVM中我们使用dual-form主要是因为传统的primal-form没有办法计算非线性的数据

假设我们遇到一个非线性的数据我们有两种解决方式

1、放弃SVM模型使用非线性模型：神经网络

2、将数据映射到高维然后进行线性分类

那么将数据映射到高维怎么能先行可分呢？如图（9）

有些数据在二维的时候并不能线性可分，我们将数据映射到三维甚至更高的的时候就可以了：

这就是一种把数据映射到高维的形式; $x=\begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix}\Rightarrow u \begin{pmatrix} x_{1} \\ x_{2} \\ x_{2}+ x_{1}\\ x_{1}-\ x_{2}\\ x_{1}\cdot x_{2}\end{pmatrix}$

但是这样构建模型就有一个问题：

假设原来的复杂度：O（n），那么映射到100维那么计算的复杂度将是原来的100倍所以为了解决这个问题我们使用了kernel Trick

首先我们将SVM由primal-form转变成dual-form

拉格朗日等号和不等号的处理

对于等号：
$min f(x)$
$st.g(x)=0$

因为在求f(x)的最优解时一定是 $\nabla f(x)||\nabla g(x)$因此 $\nabla f(x)=\lambda\nabla g(x)$

可以直接写成 $min f(x)+\lambda g(x)$

因此
$min f(x)$
$st.g_i(x)=0 \quad i=1,2,3...n$

直接写成 $min f(x)+\sum_{i=1}^n\lambda_i g_i(x)$

这是根据拉格朗日的定理

对于不等号：

$min f(x)$
$st.h(x)\leq0$

对于不等号的处理一般有两种方式：

1、没有限制条件下的最优解正好满足 $h(x)\leq0$

这个时候我们就直接 $min f(x)$的结果接可以了，我们也可以写成：

$min f(x)+\lambda h(x)$

此时
$\lambda=0$
$h(x)\leq0$

2、没有限制条件下的最优解不满足满足 $h(x)\leq0$

这个时候的最优解只能是当 $h(x)=0$的时候了也就是：
$min f(x)+\lambda h(x)$

此时
$\lambda\geq0$
$h(x)=0$

我们将两者的情况结合起来就是 $\lambda\cdot h(x)=0$

也就是：
$min f(x)+\lambda h(x)$

$st.\quad$ $\lambda\cdot h(x)=0$

KKT条件

假设我们现在有这样的一个公式：

$min f(x)$

$st.h(x)_j\leq0 \quad j=1,2,3...n$

$\quad g_i(x)=0 \quad i=1,2,3...n$

我们可以写成：
$min f(x)+\sum_{i=1}^n\lambda_i g_i(x)++\sum_{j=1}^nM_j h_j(x)$

$st.\quad\lambda_i,M_j\geq0$

$\quad \quad M_j h_j(x)=0,\forall j$

$\quad \quad h_j(x)\leq0,\forall j$

上面就是比较有名的KKT条件

SVM对应的KKT条件

这个是上面我们讨论的SVM硬目标函数（不允许有误差）

$minemize||W^T||^2$

$st:\quad (W^Tx+b )\cdot y\geq1$

我们可以转变一下：

$minemize\dfrac{1}{2}||W^T||^2$

$st:\quad 1-(W^Tx+b )\cdot y\leq0$

根据拉格朗日不等式的处理过程：

$min\dfrac{1}{2}||W||^2+\sum_{i=1}^n\lambda_i[1-(W^Tx_i+b )\cdot y_i]$

$st.\quad\lambda_i\geq0$

$\quad \quad \lambda_i[1-(W^Tx_i+b )\cdot y_i]=0,\forall i$

$\quad \quad 1-(W^Tx_i+b )\cdot y_i\leq0,\forall i$

SVM的dual-form

上面我们已经得到SVM的KKT表达式：

$min\dfrac{1}{2}||W||^2+\sum_{i=1}^n\lambda_i[1-(W^Tx_i+b )\cdot y_i]$

我们先来求出此时的梯度：

$\dfrac{\partial L}{\partial w}=0\Rightarrow W-\sum_{i=1}^n\lambda_iy_ix_i=0\Rightarrow W=\sum_{i=1}^n\lambda_iy_ix_i$

$\dfrac{\partial L}{\partial b}=0\Rightarrow \sum_{i=1}^n\lambda_iy=0$

由上式我们可以知道：

$\dfrac{1}{2}||W||^2=\dfrac{1}{2}W^T\cdot W=\dfrac{1}{2}(\sum_{i=1}^n\lambda_iy_ix_i)\cdot(\sum_{j=1}^n\lambda_jy_jx_j)=\dfrac{1}{2}\sum_{i=1}^n\sum_{j=1}^n\lambda_i\lambda_jy_iy_jx_i^Tx_j$

$\sum_{i=1}^n\lambda_i[1-(W^Tx_i+b )\cdot y_i=\sum_{i=1}^n\lambda_i-\sum_{i=1}^n\lambda_i(W^Tx_i+b )\cdot y_i$

$=\sum_{i=1}^n\lambda_i-\sum_{i=1}^n\lambda_iW^Tx_iy_i-\sum_{i=1}^n\lambda_iy_ib$

$=\sum_{i=1}^n\lambda_i-\sum_{i=1}^n\lambda_i(\sum_{j=1}^n\lambda_jy_jx_j)^Tx_iy_i=\sum_{i=1}^n\lambda_i-\sum_{i=1}^n\sum_{j=1}^n\lambda_i\lambda_jy_iy_jx_i^Tx_j$

因此我们的公式就变成：
$min\dfrac{1}{2}||W||^2+\sum_{i=1}^n\lambda_i[1-(W^Tx_i+b )\cdot y_i]=-\dfrac{1}{2}\sum_{i=1}^n\sum_{j=1}^n\lambda_i\lambda_jy_iy_jx_i^Tx_j+\sum_{i=1}^n\lambda_i$

$st.\quad\lambda_i\geq0$

$\quad \quad \lambda_i[1-(W^Tx_i+b )\cdot y_i]=0,\forall i$

$\quad \quad 1-(W^Tx_i+b )\cdot y_i\leq0,\forall i$

$\quad \quad W=\sum_{i=1}^n\lambda_iy_ix_i$

$\quad \quad \sum_{i=1}^n\lambda_iy=0$

上面就是将SVM转换成dual-from的形式

为什么要转换成这个样子呢？或者为什么要这样转换呢？

主要是因为在我们的目的让dual-from的公式中出现了 $x_i^Tx_j$

在上面我们讲过如果我们将公式映射到高维后时间复杂度会增加很多但是将数据写成 $x_i^Tx_j$我们就可以使用Kernel-Trick减少时间复杂度，甚至不增加复杂度：

举个例子：

现在有两个2维向量： $x=(x_1,x_2),z=(z_1,z_2)$
那么我们计算 $x^T\cdot z=(x_1\cdot z_1+x_2\cdot z_2)$
现在我们将向量映射到3维后：

$\phi(x)=(x_1^2,x_2^2,\sqrt{2}x_1x_2),\phi(z)=(z_1^2,z_2^2,\sqrt{2}z_1z_2)$

计算 $\phi(x)^T\cdot\phi(z)=(x_1^2z_1^2+x_2^2z_2^2,+2x_1x_2)=(x_1\cdot z_1+x_2\cdot z_2)^2=(x^T\cdot z)^2$

我们可以很清楚的看出虽然维度增加了但是复杂度还是原来的那个样子。

所以我们现在还有一个任务就是怎么设计 $\phi(x)和\phi(z)$使得 $o(\phi(x)^T\cdot\phi(z))\approx o(x^T\cdot z)$

这是一个比较复杂的过程啦，感兴趣的话可以自己查阅一下

最后我们将上面公式的推导成带有 $x^Tx$的这种形式，也就是; $k(x,y)=x^Ty$,我们称这种为线性核函数，其实还有很多核函数

例如
多项式核（Polynomial Kernel）

$k(x,y)=(1+x^Ty)^d$

高斯核（Gaussian Kernel）

$k(x,y)=e^{(\dfrac{-||x-y||^2}{2\sigma^2})}$