FOC 算法基础之欧拉公式

FOC中电压矢量合成的推导，对于欧拉公式的几何意义做了一个全面的回顾。

欧拉公式

欧拉是一个天才，欧拉公式甚至被誉为上帝创造的公式，然后在FOC算法中也可以看到欧拉公式的影子，不过因为是最基础的知识，所以基本上的换算都是一笔带过，但是如果这里没有掌握就很难搞清楚实数平面如何换算到复数平面，以至于在SVPWM的求解中存在的都是向量运算，所以这里有必要理解欧拉公式的物理意义，这样可以加深FOC算法的理解。
欧拉公式如下所示；
$\begin{cases} e^{ix} = cosx + isinx \cdots ①\\ e^{\pi i} + 1 = 0 \cdots ② \end{cases}$
这两个公式都被称之为欧拉公式；

$e$ 是自然对数的底， $i$ 是虚数（ $i=\sqrt{-1}$）。

根据式 ① 可以推导出以下另外两个变式；
推导过程如下；
令 $x = -x$，可以得到④式，如下；
$\begin{cases} e^{ix} = cosx + isinx \cdots ③\\ e^{-ix} = cosx - isinx \cdots ④\\ \end{cases}$
所以 ③ 等式左右两端与 ④ 式 相加得到；
$cosx = \cfrac{e^{ix}+e^{-ix}}{2}\cdots ⑤$
所以 ③ 等式左右两端与 ④ 式 相减得到；
$sinx = \cfrac{e^{ix}-e^{-ix}}{2i}\cdots ⑥$

几何意义

$re^{i\theta}$则表示模长为 $r$的向量旋转了角度 $\theta$，下面会进一步介绍。

复数平面

复数平面坐标 $x$轴作为实数轴， $y$轴作为虚数轴。这里可以通过欧拉公式，将实数平面换到复数平面，如下图所示；

已知这是一个半径为 $r$，圆心为 $O$的圆，则存在；
$re^{i\theta} = r(cos\theta + isin\theta)$
上式表示向量 $\overrightarrow{OP}$ 逆时针旋转了角度 $\theta$ , $| \overrightarrow{OP}| = r$；

动态过程

假设向量 $\overrightarrow{OC}$逆时针旋转，与 $x$轴夹角为 $\theta$，半径 $r = 10$，即 $| \overrightarrow{OC}| = r =10$，具体如下图所示；

这里分析一下图中的几个关键点；

• 红色点的坐标为： $(\theta, 10sin\theta)$，红色的正弦曲线为红色点的运动轨迹；
• 绿色点的坐标为； $(10cos\theta, \theta)$，绿色的正弦曲线为绿色点的运动轨迹；
• $CG$为向量 $\overrightarrow{OC}$在 $x$轴上的投影， $|CG| = 10cos\theta$；
• $CH$为向量 $\overrightarrow{OC}$在 $y$轴上的投影， $|CH| = 10sin\theta$；

可以发现，向量在复平面做圆周运动，其实数域相当于是在做正弦运动。后面再FOC中的三相正弦波形的合成可以做一下分析。

加法

欧拉公式里的相加则比较简单，相当于两个向量的相加；
$\overrightarrow{AE} = \overrightarrow{AC} + \overrightarrow{AD}$
如下图所示；

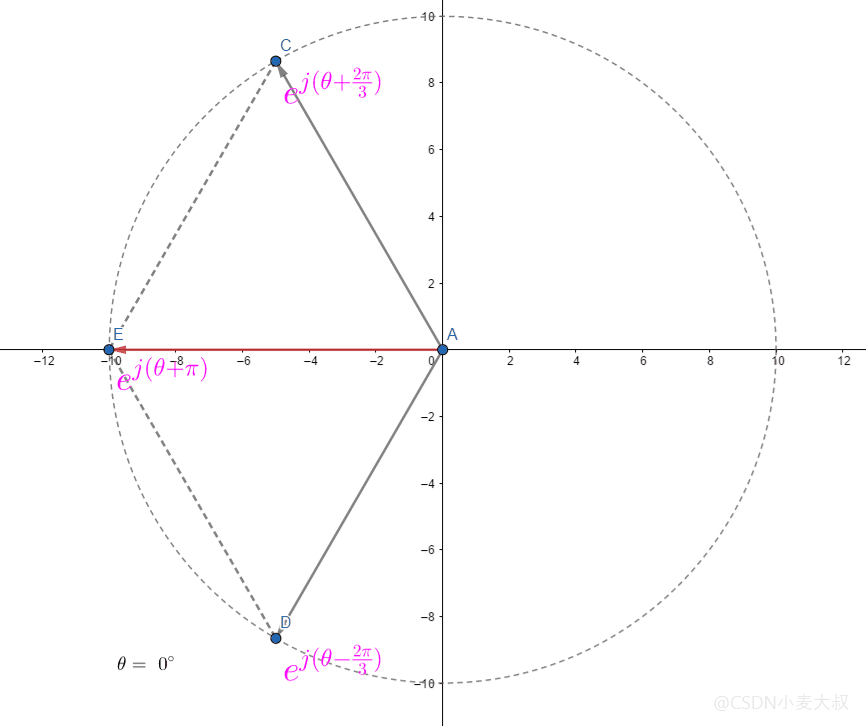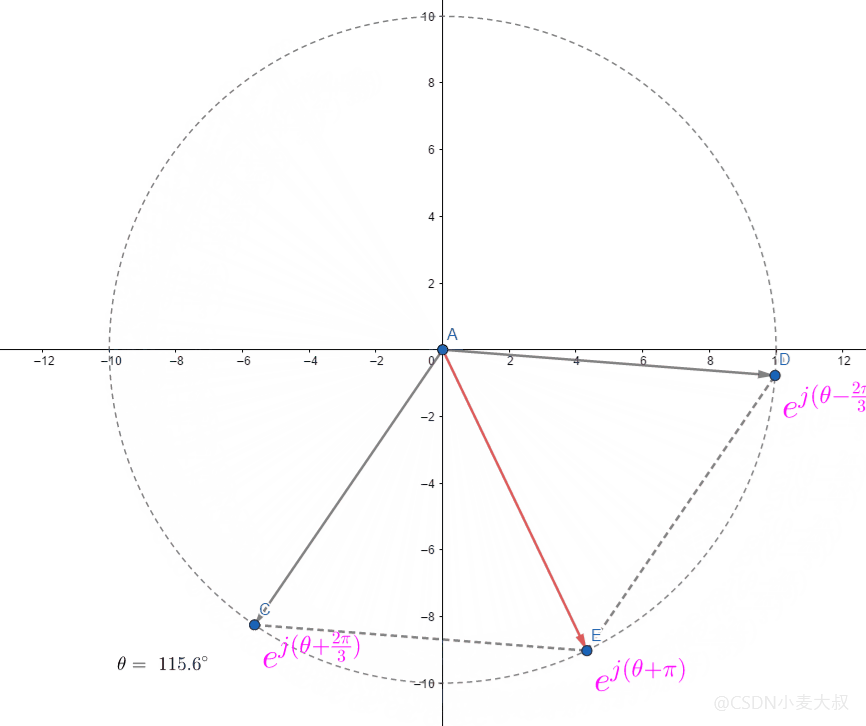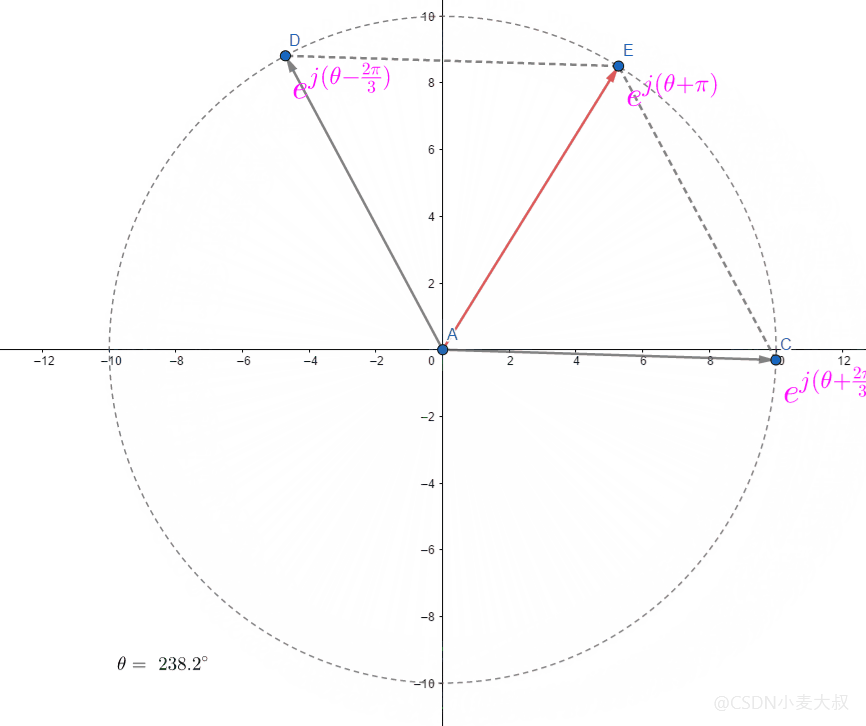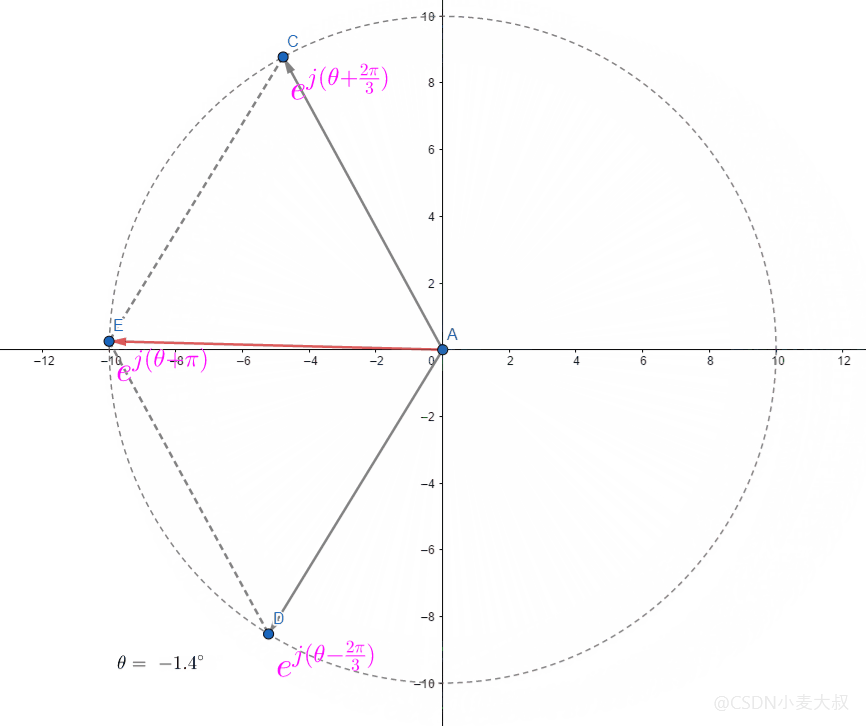
所以存在特殊情况当 $\theta = 0$时则有；
$\overrightarrow{AE} = |\overrightarrow{AE}|(e^{j(\theta+\cfrac{2\pi}{3})} + e^{j(\theta-\cfrac{2\pi}{3})} )$
直接进行符合向量相加；
$\overrightarrow{AE} = |\overrightarrow{AE}|e^{j(\theta+\pi)}$
具体如下所示；

扫描二维码关注公众号，回复： 9524853 查看本文章

FOC电压矢量的推导

三相永磁同步电机的驱动电路如下图所示；

详细的坐标变换可以参考《FOC中的Clarke变换和Park变换详解》，根据图示电路可以发现在三相永磁同步电机的驱动电路中，三相逆变输出的三相电压为 $U_{A}$， $U_{B}$， $U_{C}$将作用于电机，那么在三相平面静止坐标系ABC中，电压方程满足以下公式：

$\begin{cases} U_{A} = U_{m}cos\theta_{e} \\ U_{B} = U_{m}cos(\theta_{e} - \cfrac{2\pi}{3}) \\ U_{C} = U_{m}cos(\theta_{e} + \cfrac{2\pi}{3}) \end{cases}$

$U_m$为相电压基波峰值；

因此根据前面式⑤ $cosx = \cfrac{e^{ix}+e^{-ix}}{2}\cdots ⑤$
可以将该方程组转换到复平面可以得到，下式统一使用 $\theta$ 表示 $\theta_{e}$；
$\begin{cases} U_{A}= U_{m}cos\theta_{e} = \cfrac{ U_{m}}{2}(e^{i\theta} + e^{-i\theta})\\ U_{B}= U_{m}cos(\theta_{e} + \cfrac{2\pi}{3}) = \cfrac{ U_{m}}{2}(e^{(i\theta-\cfrac{2\pi}{3})} + e^{-(i\theta-\cfrac{2\pi}{3})})\\ U_{C} = U_{m}cos(\theta_{e} - \cfrac{2\pi}{3}) = \cfrac{ U_{m}}{2}(e^{(i\theta+\cfrac{2\pi}{3})} + e^{-(i\theta+\cfrac{2\pi}{3})}) \end{cases}$
因为需要将三相电压合成矢量 $\overrightarrow{U} = \overrightarrow{U_A} + \overrightarrow{U_B} + \overrightarrow{U_C}$；下面增加向量的相位差；
$\begin{cases} \overrightarrow{U_A} = U_A *e^{j0}\\ \overrightarrow{U_B} = U_B *e^{-(j\cfrac{2\pi}{3})} \\ \overrightarrow{U_C} = U_C *e^{(j\cfrac{2\pi}{3})}\\ \end{cases}$

中间推导过程暂略，最终推导得到；
$\overrightarrow{U} = \cfrac{3}{2}U_me^{j\theta} = \cfrac{3}{2}U_me^{j\omega t}$

总结

磕磕绊绊写了最后，基础学科的掌握还不够，很多知识回过头来看，总会有新的收获，但是由于笔者能力有限，文中难免出行错误和纰漏，望您能不吝赐教。

参考

https://www.matongxue.com/madocs/8.html