（4.3）树与二叉树之二叉排序树的变形

1.二叉树可以变形的种类

• 二叉排序树（BST）
• 平衡二叉树(AVL)
• 哈夫曼树及哈夫曼编码
• 堆排序

2.二叉排序树BST

• 定义：
  若根节点的左子树不为空，则左子树上所有节点的值都小于根节点的值；
  若根节点的右子树不为空，则右子树上所有节点的值都大于根节点的值；
  左子树和右子树本身就是一颗二叉排序树；
  与二叉树定义类似，都是递归的定义
• eg：
  采用中序遍历可以得到一个有序的序列，可以作为判断二叉排序数的方法
  
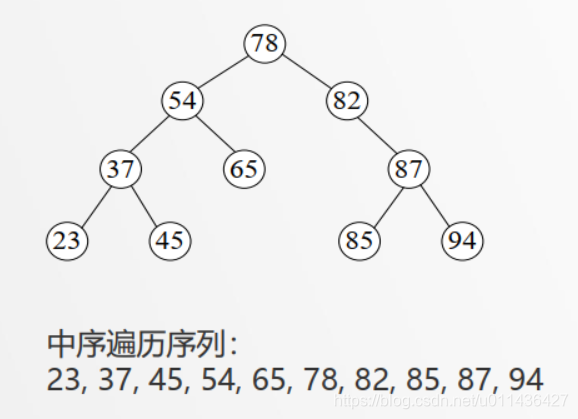
• eg:
  
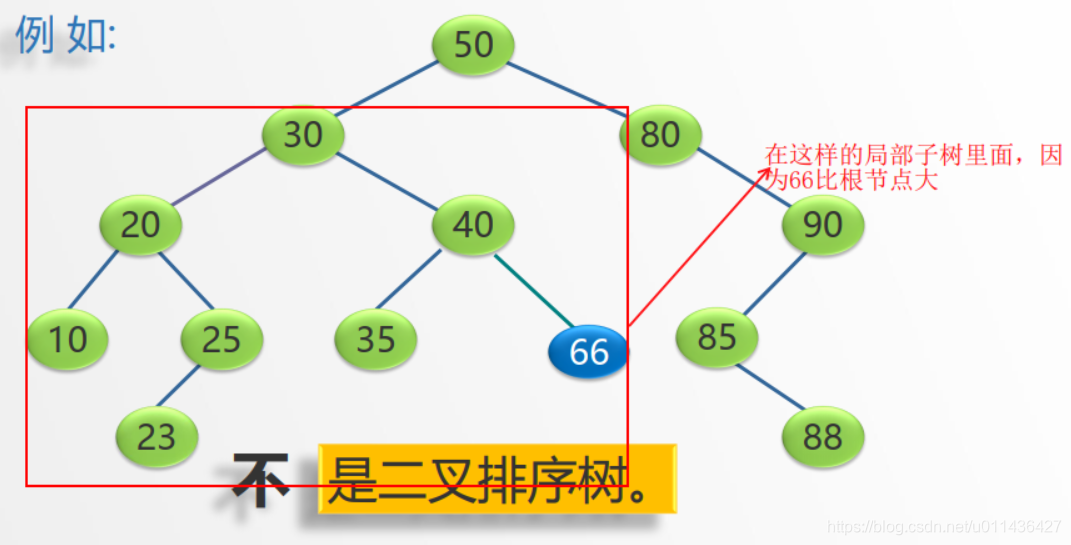
• 二叉排序树的查找
  与根节点比较，比他大往右走，比他小，往左走
  
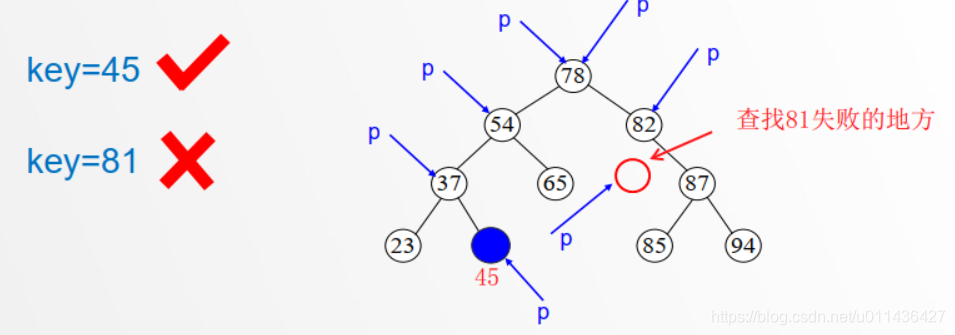
• 二叉排序树的插入算法
  插入操作在查找不成功时才进行；

当二叉排序树中不存在关键字等于 e.key 的数据元素时，插入元素值为 e 的结点，并返回 TRUE; 
否则，不进行插入并返回FALSE

typedef struct BiTreeNode
{
	Datatype data;
	struct BiTreeNode *lchild, *rchild, *parent;
}BiTreeNode, *BiTree;

Status Insert BST(BiTree &T, ElemType e)
{
	//查找失败的情况下，才插入
	if (!SearchBST(T, e.key,p))
	{
		//准备待插入的节点
		s=(BiTree)malloc(sizeof(BiTNode));//为新节点分配空间
		s->data=e;
		s->lchild=s->rchild=NULL;

		if (!p)//若是空的二叉排序树
			T=s;
		else if (e.key < p->data.key)//p->data.key为当前节点的值
			p->lchild=s;//插入 *s 为 *p 的左孩子
		else
			p->rchild=s;//插入 *s 为 *p 的右孩子
		
		return TRUE;//插入成功
	}
	else
		return FALSE;		
}

• 二叉排序树的删除算法，删除可分三种情况讨论：
  （1）被删除的结点是叶子
  （2）被删除的结点只有左子树或者只有右子树
  （3）被删除的结点既有左子树， 也有右子树

（1）被删除的结点是叶子结点，核心：其双亲结点中相应指针域的值改为“空”
删除节点20：
从根节点开始，查找到20这个节点，让他的双亲节点由f指针指向，释放点20这个节点，同时修改30节点的左指针域为空。

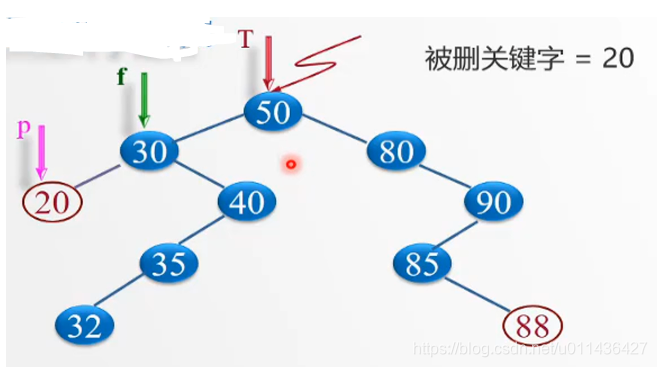
（2）被删除的结点只有左子树或者只有右子树，核心：其双亲结点的相应指针域的值改为 “指向被删除结点的左子树或右子树”。
p指向待删除节点，f指向双亲节点，
删除掉40节点后，应该让子树重新连接到40节点的双亲节点30的右子树域，这样就完成了节点40的删除

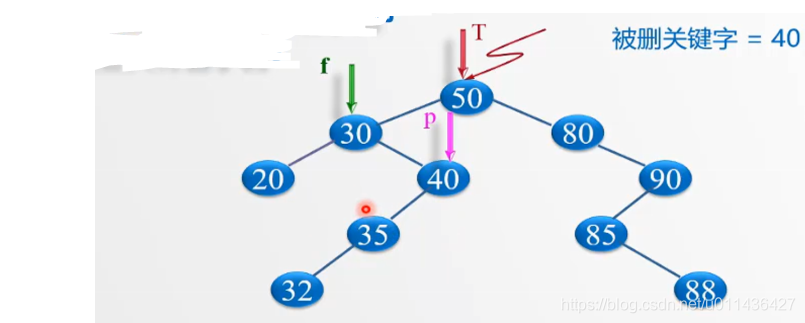
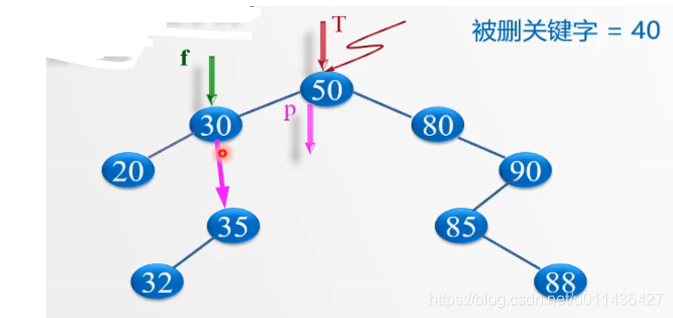
（3）被删除的结点既有左子树，也有右子树：核心是：以其前驱替代之，然后再删除该前驱结点
因为中序遍历后会得到有序序列，50的前驱节点是40，让前驱节点40去替换50，然后将前驱节点进行删除，将其子树
进行重连


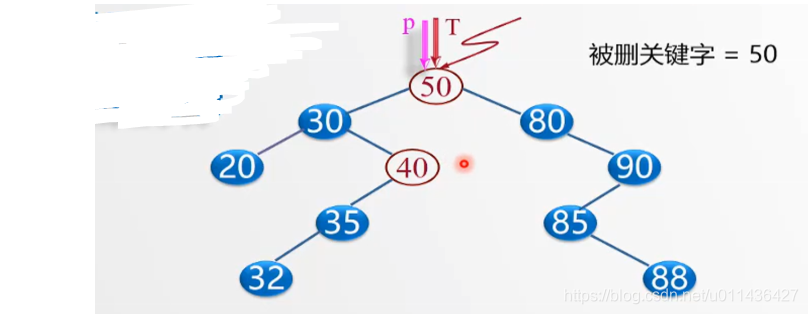
具体算法描述如下：

typedef struct BiTreeNode
{
	Datatype data;
	struct BiTreeNode *lchild, *rchild, *parent;
}BiTreeNode, *BiTree;

Status DeleteBST(Bitree &T, KeyType key)
{
/* 若二叉排序树 T 中存在其关键字等于 key 的*/
/* 数据元素，则删除该数据元素结点，并返回*/
/*函数值 TRUE，否则返回函数值 FALSE*/
if (!T)//若是空树
	return FALSE;
else
	{
		if (key==T->data.key)
		{
			Delete(T);
			return TRUE;
		}
		else if(key<T->data.key)
			DeleteBST ( T->lchild, key );
			/* 继续在左子树中进行查找*/
		else
			DeleteBST ( T->rchild, key );
			/*继续在右子树中进行查找*/
	}
}/* DeleteBST*/

其中删除操作过程如下所描述：
void Dele(Bitree &p)
{
	/* 从二叉排序树中删除结点 p， */
	/* 并重接它的左子树或右子树*/
	if(!p->lchild && p->rchid)  
		free(&p);//若左右节点都为空
	else if(!p->rchid)/*只有左子树*/
	{/* 右子树为空树则只需重接它的左子树*/}
	else if (!p->lchid)/*只有右子树*/
	{* 左子树为空树只需重接它的右子树*/}
	else/*左右子树均有*/
	{
	/* 左右子树均不空*/
	}
}

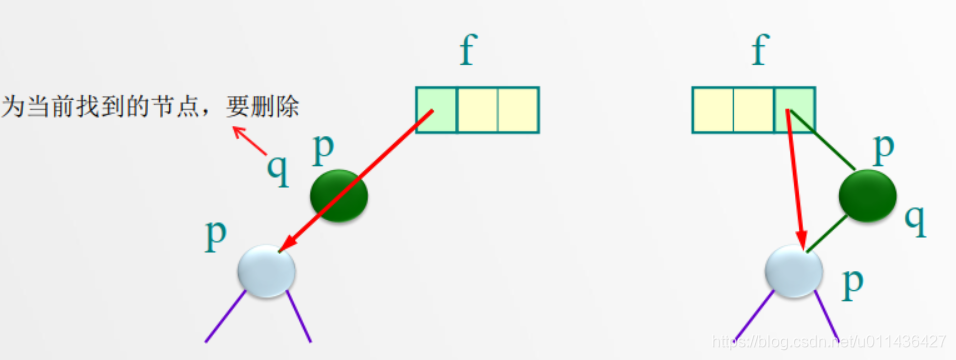
{/* 右子树为空树则只需重接它的左子树*/}的描述如下：

左边情况的代码为：
q=p；
p=p->lchild;
f->lchild=p;
free(q);

左边情况的代码为：
q=p；
p=p->lchild;
f->rchild=p;
free(q);

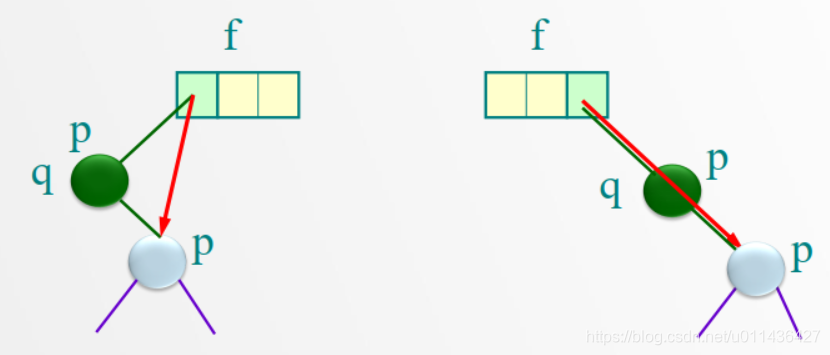
/* 左子树为空树只需重接它的右子树*/的描述如下：

左边情况的代码为：
q=p；
p=p->rchild;
f->lchild=p;
free(q);

左边情况的代码为：
q=p；
p=p->rchild;
f->rchild=p;
free(q);

/* 左右子树均不空*/的描述如下：

q = p; s = p->lchild;
//待删除节点的前驱节点的定位操作
while(s->rchild)
{
	q=s;
	s=s->rchild;/* s 指向被删结点p的前驱,q与s同步*/
}
p->data = s->data;//让前驱节点覆盖当前被删除节点

//重连操作
if (q != p ) ///* 重接*q的左子树*/
	q->rchild = s->lchild;
else 
	q->lchild = s->lchild;
free(s);//S的内容已复制到P上，即P实际上已变成S*/

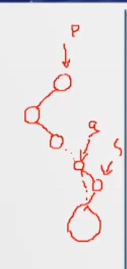
//待删除节点的前驱节点的定位操作的解释如下：
p节点是待删除节点，让s节点指向其左孩子，让while循环不停的找右孩子，直到找到s节点，其双亲节点用q指向，
经过若干步之后，s节点就没有右子树了，若他还有右子树的话，他就不会是p节点的前驱节点(按照中序遍历的思想去想)

//重连操作的解释如下：
按照上述的解释q！=p，所以可以直接进行重连操作；
若只有左子树，不存在右子树的话，s位置只能是如下图所示的位置，此时p和q同时指向被删除节点

• 查找性能的分析
  （1）例如：由关键字序列 1， 2， 3， 4， 5构造而得的二叉排序树，
  ASL =（1+2+3+4+5） / 5= 3
  
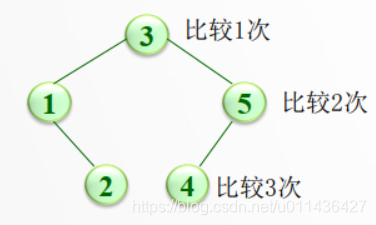
  （2）由关键字序列 3， 1， 2， 5， 4构造而得的二叉排序树
  ASL =（1+2+3+2+3） / 5= 2.2