github:https://github.com/MichaelBeechan
CSDN:https://blog.csdn.net/u011344545
=======================================
算法 | 卡尔曼滤波器算法1——应用介绍(Matlab & simulink)
单片机开发 | 基于51单片机实现MPU6050的卡尔曼滤波算法(代码类)
单片机开发 | 基于MPU6050的卡尔曼滤波算法(代码类)
======================================
Kalman滤波算法的提出也是为了解决实际问题,斯坦利·施密特(Stanley Schmidt)首次实现了卡尔曼滤波器。
Kalman滤波经过几十年的发展,形成了适用于不同领域的算法,有线性滤波,非线性滤波,以及扩展的Kalman滤波、无迹卡尔曼滤波、自适应卡尔曼滤波等。
卡尔曼滤波通过递推运算,用先验值和最新观测数据中得到的新值进行加权平均来估计系统参数,比如位置、速度、姿态等。
它是在存在不确定性的情况下组合信息的一种通用且强大的工具。(powerful tool for combining information in the presence of uncertainty)
您可以在任何有关某些动态系统的不确定信息的地方使用卡尔曼滤波器,并且您可以对系统下一步要做什么做出有根据的猜测。 即使出现凌乱的现实并干扰您猜测的清洁运动,卡尔曼滤波器通常也能很好地弄清楚究竟发生了什么。 它可以利用您可能不会想到的疯狂现象之间的相关性!
卡尔曼滤波器是不断变化的系统的理想选择。 它们的优势在于它们对内存的依赖性很强(它们不需要保留除前一状态之外的任何历史记录),并且它们非常快,使它们非常适合实时问题和嵌入式系统。
理解卡尔曼滤波算法的先决条件很简单:您所需要的只是对概率和矩阵的基本理解。由描述状态向量的过程方程和描述观测向量的观测方程共同表示。
1、过程方程
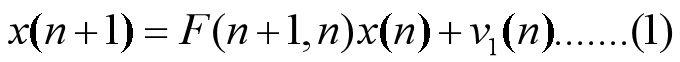
式中:向量x(n)表示系统在离散时间n的状态向量,它是不可观测的;矩阵F(n+1,n)称为状态转移矩阵,描述动态系统在时间n的状态到n+1的状态之间的转移,为已知量;向量 v1(n)为过程噪声向量,它描述状态转移中间的加性噪声或误差。
2、观测方程
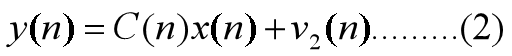
式中:向量y(n)表示动态系统在时间n的观测向量;矩阵C(n)称为观测矩阵(描述状态经过其作用,变成可预测的),要求也是已知的;v2(n)表示观测噪声向量,其维数与观测向量的相同。过程方程也称为状态方程,为了分析的方便,通常假定过程噪声v1(n)和观测噪声v2(n)均为零均值的白噪声过程,它们的相关矩阵分别为:
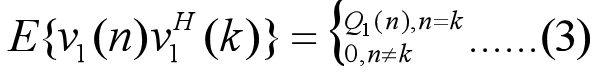
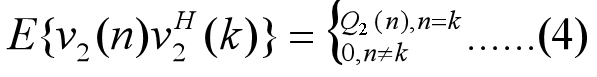
噪声向量v1(n)与v2(n)也不相关
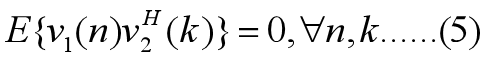
3、新息过程
考虑一步预测问题,给定观测值y(1), …,y(n-1),求观测向量y(n)的最小二乘估计,记作
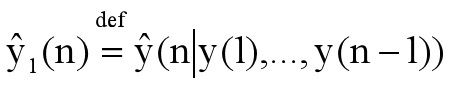
y(n)的新息过程定义为:
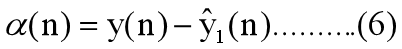
向量a(n)表示观测数据y(n)的新的信息,简称新息。
3.1 新息a(n)具有以下性质:
性质1 n时刻的新息a(n)与所有过去的观测数据y(1), …,y(n-1)正交,即:
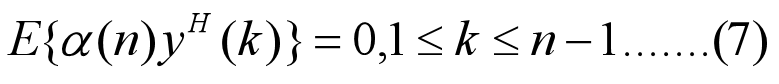
性质2 新息过程由彼此正交的随机向量序列{a(n)} 组成,即有
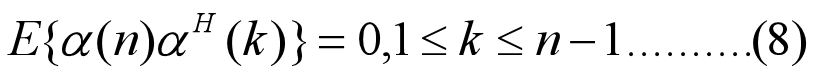
性质3 表示观测数据的随机向量序列{y(1) ,…y(n)}与表示新息过程的随机向量序列{a(1),…a(n)} 一一对应 ,即
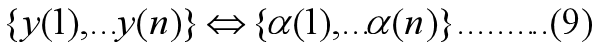
以上性质表明:n时刻的新息a(n)是一个与n上课之前的观测数据y(1), …,y(n-1)不相关,并具有白噪声性质的随机过程,但它却能够提供有关y(n)的新息,这就上信息的内在物理含义。
3.2 新息过程的计算
下面分析新息过程的相关矩阵
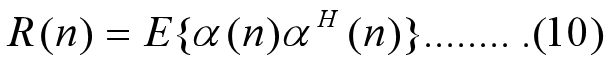
在kalman滤波中,并不直接估计观测数据向量的进一步预测,而是先计算状态向量的一步预测
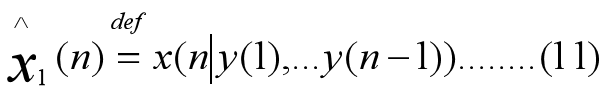
然后再用到下式得到
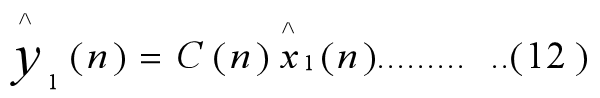
将上式代入新息过程的定义式(6),可得到:
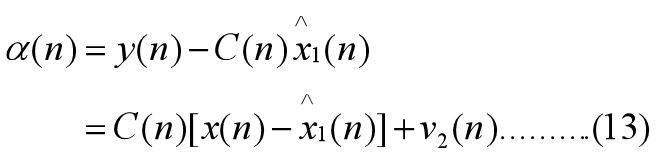
这就是新息过程的实际计算公式,条件是:一步预测的状态向量估计x1(n)也已求出。
定义向量的一步预测误差:
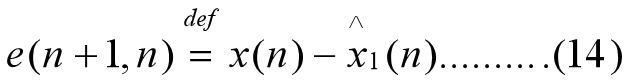
将此式代入式(13),则有
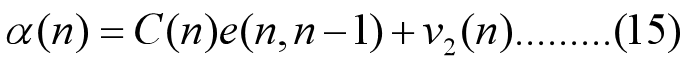
在新息过程的相关矩阵定义式(10)中代入式(14),并注意到观测矩阵C(n)是一已知的确定矩阵,故有
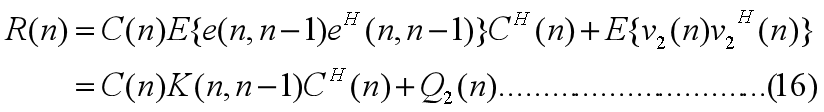
式中Q2(n)是观测噪声v2(n)的相关矩阵,而
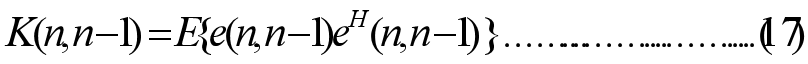
表示(一步)预测状态误差的相关矩阵。
(待续。。。。。。。。。。。。。。。。。。。。。。)
Kalman滤波器是一种线性的离散时间有限维系统。Kalman滤波器的估计性能是:它使滤波后的状态估计误差的相关矩阵P(n)的迹最小化。这意味着,kalman滤波器是状态向量x(n)的线性最小差估计。
kalman滤波算法的结构图如下:
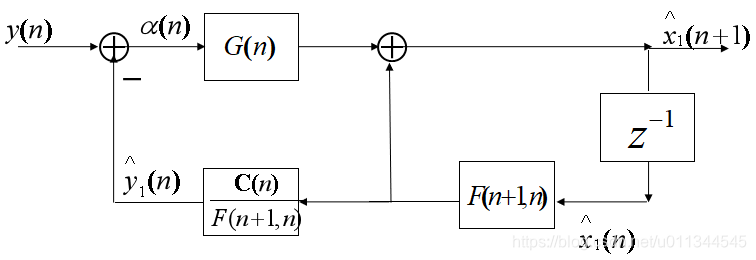
4、卡尔曼滤波的理论假设
卡尔曼滤波算法是以估计值为真值的无偏估计为目标,以实现各个变量的方差最小化,然后对系统状态参数、预测观测值及新息进行预测。
(1) 滤波估计值是对先验预测估计值以及观测量估计值的线性叠加(加权平均);
(2)状态转换矩阵呈线性;
(3)状态估计值服从高斯分布;
(4)观测值概率密度服从高斯分布;
(5)过程噪声和观测均为白噪声,是均值为0的高斯噪声。
卡尔曼滤波理论基础是状态变量的预测估计值以及观测量的后验估计值均为高斯分布;基于二者线性叠加(加权平均)的最终状态变量估计值也为高斯分布;建立的状态预测方程和观测方程均为线性函数。
5、观测噪声及其协方差矩阵
观测噪声服从均值为零的高斯分布,有两个途径进行确定:
(1)将观测系统的动力系统和设备噪声假设为常量,协方差矩阵也是常量矩阵;
(2)建模为动力学/信噪比测量的函数。
在卡尔曼滤波算法迭代过程中,协方差矩阵是实际观测向量和状态向量先验估计值计算的观测向量之间的误差协方差。
6、卡尔曼滤波增益矩阵的意义
增益矩阵决定了观测信息在状态向量更新时的权重,是卡尔曼滤波算法的关键。根据卡尔曼滤波增益的表达可知受两个因素的影响:状态误差协方差(正相关)、实际观测向量的误差协方差矩阵(负相关)、状态向量先验估计值预测的观测向量误差协方差矩阵(负相关)。当状态向量先验估计值的不确定度下降,则状态误差协方差矩阵会变小,意味着卡尔曼增益下降,使得状态向量后验估计更依赖于先验估计值,状态不确定度降低的速度会变慢,最后接近一个平衡值。当实际观测向量的误差变小,或者状态向量先验估计值预测的观测向量误差变小,意味着卡尔曼增益上升,使得状态向量后验估计更依赖于观测值。因此,卡尔曼增益矩阵通过对观测信息的加权,实现了信息从观测空间到状态空间的转移。
(待续。。。。。。。。。。。。。。。)
参考链接:
https://mp.weixin.qq.com/s/1zfljTczRMIMpmkuEJbWaQ (卡尔曼滤波算法分析)
https://www.bzarg.com/p/improving-imu-attitude-estimates-with-velocity-data/
http://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/
